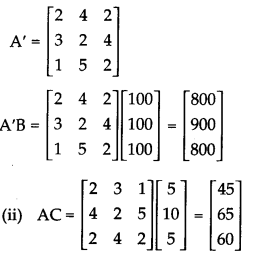CBSE Sample Papers for Class 12 Maths Set 4 with Solutions

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Set 4 with Solutions

Time Allowed: 3 hours
Maximum Marks: 70

General Instructions:

1. This question paper contains five sections – A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section – A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section – B has 5 Very Short Answer (VSA)-type questions of 2 marks each.
4. Section – C has 6 Short Answer (SA)-type questions of 3 marks each.
5. Section – D has 4 Long Answer (LA)-type questions of 5 marks each.
6. Section – E has 3 source based/case based/passage based/integrated units of assessment (4 marks each) with sub parts.
7. Section – A
   (Multiple Choice Questions) Each question carries 1 mark

Question 1.
If x is real, then the minimum value of x²2 – 8x + 17 is :
(a) -1
(b) 0
(c) 1
(d) 2
Answer:
(c) 1
Explanation:
Let f(x) = x² – 8x + 17
∴ f'(x) = 2x – 8
So, f'(x)= 0, gives x = 4
Now, f'(x) = 2 > 0, ∀ x
So, x = 4 is the point of local minima.
∴ Minimum value of fix) = at x = 4.
f(4) = 4 × 4 – 8 × 4 + 17 = 1.

Question 2.
If s(x) = \(\left|\begin{array}{ccc}0 & x-a & x-b \\x+a & 0 & x-c \\x+b & x+c & 0\end{array}\right|\) then:
(a) f(a) = 0
(b) f(b) = 0
(c) f(c) = 0
(d) f(1) = 0
Answer:
(c) f(c) = 0
Explanation:

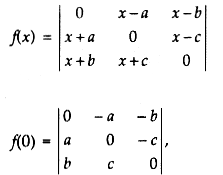
which is skew-symmetric determinant of order 3
Hence, f(O) = 0

Question 3.
If \(A=\left[\begin{array}{ll}2 & 3 \\1 & 2\end{array}\right], B=\left[\begin{array}{lll}1 & 3 & 2\\4 & 3 & 1\end{array}\right], C=\left[\begin{array}{l}1 \\2\end{array}\right]\) and \(\mathrm{D}=\left[\begin{array}{lll}4 & 6 & 8 \\5 & 7 & 9\end{array}\right]\), then which
of the following is defined?
(a) A + B
(b) B + C
(c) C + D
(d) B + D
Answer:
(d) B + D
Explanation:
Only B + D is defined because matrices of the same order can only be added.

Question 4.
The degree of the different equation \(\frac{d^2 y}{d x^2}+3\left(\frac{d y}{d x}\right)^2=x^2 \log \left(\frac{d^2 y}{d x^2}\right)\) is :
(a) 1
(b) 2
(c) 3
(d) Not defined
Answer:
(d) Not defined
Explanation:
The given different equation is not a polynomial equation in terms of its derivatives, so its degree is not defined.

Question 5.
\(\int x^{51}\left(\tan ^{-1} x+\cot ^{-1} x\right) dx\)
(a) \(\frac{x^{52}}{52}\)(tan^-1 x + cot^-1 x) + C
(b) \(\frac{x^{52}}{52}\)(tan^-1 x + cot^-1 x) + C
(c) \(\frac{\pi x^{52}}{104}+\frac{\pi}{2}+C\)
(d) \(\frac{x^{52}}{52}+\frac{\pi}{2}+C\)
Answer:
(a) \(\frac{x^{52}}{52}\)(tan^-1 x + cot^-1 x) + C
Explanation:
\(\int x^{51}\left(\tan ^{-1} x+\cot ^{-1} x\right) dx\)
\(\int x^{51} \cdot \frac{\pi}{2} d x\)
\(\frac{\pi x^{52}}{104}+C\) = \(\frac{x^{52}}{52}\)(tan^-1x + cot^-1x) + C

Question 6.
The number of points at which the function f(x) = \(\frac{1}{x-[x]}\) where [ ] denotes the greatest integer function is not contaiuous:
(a) 1
(b) 2
(c) 3
(d) None od these
Answer:
(d) None od these
Explanation:
x – [x] = 0 when x is an integer, so that f(x) is discontinuous for all x ∈ I i.e., f{x) is discontinuous at infinite number of points.

Question 7.
The greatest value of 5 sin ² x + 7 cos² x – 4 sin x cos x will be:
(a) 6 – √5
(b) 6 + √5
(c) -6 + √5
(d) -6 -√5
Answer:
(b) 6 + √5
Explanation:
y = 5 sin²x + 7 cos²x – 4 sin x cos x
= (2 sin x – cos x)² + sin²x + 6 cos² x
= (2 sin x – cos x)² + (sin²x + cos² x) + 5 cos² x
y_max x = \(\left(\sqrt{2^2+(1)^2}\right)\) + 1 + 5
= 6 + √5

Question 8.
Feasible region in the set of points which satisfy:
(a) The objective functions
(b) Some of the given functions
(c) All of the given constraints
(d) None of these
Answer:
(c) All of the given constraints
Explanation:
Feasible region is the ser of point which satisfies all the give constraints

Question 9.
The matrix P = \( \left[\begin{array}{lll}0 & 0 & 4 \\0 & 4 & 0 \\4 & 0 & 0\end{array}\right]\) is not a:
(a) square matrix
(b) diagonal matrix
(c) unit matrix
(d) none of these
Answer:
(c) unit matrix
Explanation:
If square matrix in which all diagonals elements are 4 and rest are 0, is called unit matrix.

Question 10.
Find the integer of \(\sqrt{u}+\frac{1}{\sqrt{u}}\)
(a) \(\frac{2}{3}\)u^3/2 + 2u^1/2 + C
(b) \(\frac{2}{3}\)u^3/2 – 2u^1/2 + C
(c) –\(\frac{2}{3}\)u^3/2 – 2u^1/2 + C
(d) –\(\frac{2}{3}\)u^3/2 + 2u^1/2 + C
Answer:
(a) \(\frac{2}{3}\)u^3/2 + 2u^1/2 + C
Explanation:

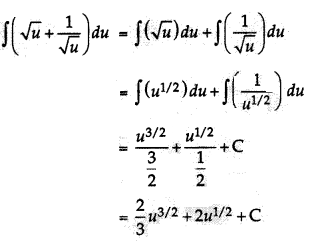
Question 11.
Which of the term is not used in a linear programming problem?
(a) Optimal solution
(b) Feasible solution
(c) Concave region
(d) Objective function
Answer:
(c) Concave region

Question 12.
The domain of the function cos^-1(2x – 1) is:
(a) [0, 1]
(b) [-1, 1]
(c) (-1, 1)
(d) [0, π]
(a) [0, 1]
Answer:
(a) [0, 1]
Explanation:
We know that cos^-1x is defined for x ∈ [-1, 1]
∴ f(x) = cos^-1 (2x – 1) is defined if
-1 ≤ 2x – 1 ≤ 1
⇒ 0 ≤ 2x ≤ 2
⇒ 0 ≤ x ≤ 1

Question 13.
Minor of an elements of a determinant of order n(n ≥ 2)is a determinant of order:
(a) n
(b) n – 1
(c) n – 2
(d) n + 1
Answer:
(b) n – 1
Explanation:
Minor of on elements is the determinant obtained by leaving the elements of the column and row containing that element. Therefore, miror of an element of a determinant of order n is a determinant of order n – 1.

Question 14.
If A is a 3 × 2 matrix, B ia a 3 × 3 matrix and C is a 2 × 3 matrix thrn elements in A,B and C are respectively:
(a) 6,9,8
(b) 6,9,6
(c) 9,6,6
(d) 6,6,9
Answer:
(b) 6,9,6
Explanation:
The number of elements in m × n matrix is equal to mn
∴ elements in A = 3 × 2 = 6
∴ elements in B = 3 × 3 = 9
∴ elements in C = 2 × 3 = 6

Question 15.
The order and degree of differential equation \(\left[1+\left(\frac{d y}{d x}\right)^2\right]\) = \(\frac{d^2 y}{d x^2}\) are:
(a) 2,\(\frac{3}{2}\)
(b) 2,3
(c) 2,1
(d) 3,4
Answer:
(c) 2,1
Explanation:
Given that,
\(\left[1+\left(\frac{d y}{d x}\right)^2\right]\) = \(\frac{d^2 y}{d x^2}\)
∴ Order = 2 and degree = 1

Question 16.
The function f(x) = tan x is discontinuous on the set:
(a) {x = nπ : n ∈ Z}
(b) {x = 2nπ : n ∈ Z}
(c) \(\left\{x=(2 n+1) \frac{\pi}{2} ; n \in Z\right\}\)
(d) \(\left\{x=\frac{n \pi}{2} ; n \in Z\right\}\)
Answer:
(c) \(\left\{x=(2 n+1) \frac{\pi}{2} ; n \in Z\right\}\)
Explanation:
when tan (2n + 1)\(\frac{\pi}{2}\) = tan \(\left(n \pi+\frac{\pi}{2}\right)\) = -cot nπ
lt is not defined at the integral points (n ∈ Z)
Hence,f(x) is discontinuous at (2n + l)— \(\frac{\pi}{2}\)

Question 17.
Which one of the following is correct in respect of the function,f(x) = x³ sin x?
(a) It has local maximum at x = 0
(b) It has local minimum at x = 0
(c) It has neither maximum nor minimum at x = 0
(d) It has maximum value as 1 Sol. (b) It has local
Answer:
(b) It has local minimum at x = 0
Explanation:
Given
f(x) = x³ sin x
∴ f'(x) = x³ cos x + 3x² sin x
Now, f”(x) = -x³ sin x + 3x²cos x – 6x sin x
For critical points f'(x) = 0
⇒ x³cos x – 3x²sin x = 0
⇒ x²(x cos x – sin x) = 0
∴ x = 0
At x = 0
⇒ f”(x) = 0
⇒ Function has local minimum at x = 0

Question 18.
The general solution of the differential equation \(\frac{d y}{d x}\) = cot x cot y is :
(a) cos x = C cosec Y
(b) sin x = C sec y
(c) sin x = C cos y
(d) cos x = C sin y
Answer:
(b) sin x = C sec y
Explanation:
\(\frac{d y}{d x}\) = cot x cot y
⇒ cot x dx – tan y dy = 0
Instructions both sides, we get
⇒ ∫cot x dx – tan y dy = 0
log sin x – log sec y = log C
⇒ log \(\left(\frac{\sin x}{\sec y}\right)\) = log C
⇒ sin x = C sec y.

Question 19.
Assertion (A): Values of k for which area of the triangle with vertices (1,1), (0, 2), (k, 0) is 3 sq. units are 4 and 8.
Reason :
Area of the triangle with vertices (x₁,y₁),(x₂,y₂),(x₂,y₂),(x₃,y₃)is \(\frac{1}{2}\)\(\left|\begin{array}{lll}x_1 & y_1 & 1 \\x_2 & y_2 & 1 \\x_3 & y_3 & 1\end{array}\right|c\)
Answer:
(d) A is false but R is true.
Explanation:
A is false but R is true.
Area of triangle with vertices (1,1), (0, 2), (k, 0) is 3 sq. units.
\(\frac{1}{2}\left|\begin{array}{lll}1 & 1 & 1 \\0 & 2 & 1 \\k & 0 & 1\end{array}\right|\)
⇒ 1(2 – 0) – 1(0 – k) + 1(0 – 2K) = 6
⇒ 2 + K – 2K = 6
⇒ -k = 6 – 2
⇒ K = 4
∴ value of k is : 4

Question 20.
Assertion (A): The scalar product of a force \(\overrightarrow{\mathrm{F}}\) and displacement \(\vec{r}\) is equal to the work done.
Reason (R): Work done is not a scalar.
Answer:
(c) A is true but R is false.
Explanation:
Work done, W = \(\overrightarrow{\mathrm{F}} \cdot \vec{r}\)
∴ Work done is a Scalar quantity.

Section – B
[This section comprises of very short answer type-questions (VSA) of 2 marks each]

Question 21.
Write the values of cos 1 cos_-1 \(\left(\cos \frac{7 \pi}{6}\right)\)
Using principal values, evaluate tan^-1 (1) + sin^-1 \(\left(-\frac{1}{2}\right)\)
Answer:
We know that the principal value of cos_-1 θ is [0, n]

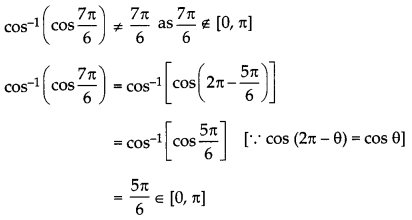
Or

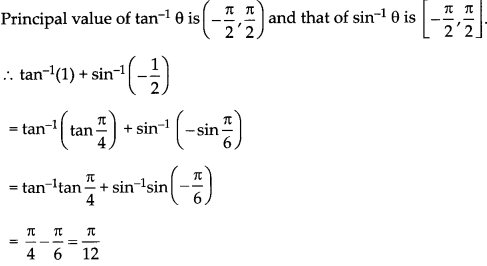
Question 22.
If the radius of a sphere is measured as 9 cm with an error of 0.03 cm, then find the approximate error in calculating its volume.
Answer:
Let r be the radius of the sphere and Ar be the error in measuring the radius. Then r = 9 cm and Ar = 0.03 cm. Now, the volume V of the sphere is given by
V = \(\frac{4}{3}\)πr₃
or
\(\frac{d \mathrm{~V}}{d r}\) = 4πr₂
∴ dV = \(\left(\frac{d \mathrm{~V}}{d r}\right)\)∆r = 4πr₂
= 4π(9)₂(0.03)
= 9.72π cm₃
Thus, the approximate error in calculating the volume is 9.727c cm₃.

Question 23.
An expensive square piece of golden colour board of side 24 centimetres, is to be made into a box by cutting a square from each comer and folding the flaps to form a box. What should be the side of the square piece to be cut from each comer of the board to hold maximum volume and minimise the wastage?
OR
Find the intervals in which the function f(x) = \(\frac{x^4}{4}\) x³ – 5x² + 24x + 12 is (i) strictly increasing, (ii) strictly decreasing.
Answer:
Let length of a side of the square cut out = c cm
Volume, V = (24 – 2x)²x
\(\frac{d \mathrm{~V}}{d x}\) = 2(24 – 2x)(-2)x + (24 – 2x)²
= (24 – 2x)(-4x + 24 – 2x)
= (24 – 2x) (24 – 6x)
= 12(12- x)(4 – x)
put \(\frac{d \mathrm{~V}}{d x}\) = 0 i.e., (12 – x)(4 -x) = 0
Since, x ≠ 12,
∴ x = 4

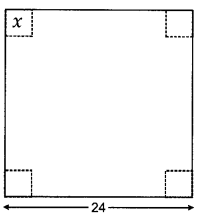
Hence, the volume will be maximum when length of a side of the square cut out = 4 cm.
OR
Given function is
f(x) = \(\frac{x^4}{4}\) – x³ – 5x² + 24x + 12
⇒ f'(x) = \(\frac{x^4}{4}\) – 3x² – 10x + 24
For critical points, put f'(x) = 0
∴ x³-3x² – 10x + 24 = 0
(x – 2)(x² – x – 12) = 0
(x – 2)(x – 4) (x + 3) = 0
x = 2, 4, -3
Therefore, we have the intervals (- ∞, – 3), (- 3, 2), (2, 4) and (4, ∞).

Since f'(x) > 0 in (-3, 2) ∪ (4,∞).
∴f(x) is decreasing in interval (-3,2)∪(4,∞).
And f(x) < 0 in (-∞,-3)∪(2,4)

Question 24.
Solve the following differential equation :
e^x tan y dx + (1 – e^x) sec² y dy = 0
Answer:
Given differential equation is,
e^x tan y dx + (1 – e^x) sec² y dy = 0
⇒ (1 – e^x) sec² y dy = -e^x tan y dx

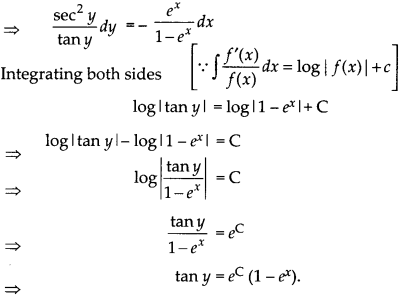
Which is the required solution.

Question 25.
In a kite festival, a kite is at a height of 120 cm and 130 m string is out. If the kite is moving horizontally at the rate of 5.2 m/sec, find the rate at which the string is being pulled out at that instant.
Answer:
Let at any instant,
Length of string = y m
and horizontal distance of the kite = x m
then \(\frac{d x}{d t}\) = 5.2 m/sec
Then, y² = x² + (120)²
Differentiate above equation w.r.t. t

Section – C
[This section comprises of short answer type questions (SA) of 3 marks each]

Question 26.
Evaluate \(\int \frac{x^3 \sin \left(\tan ^{-1} x^4\right)}{1+x^8} dx\)
Answer:

Question 27.
Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below :
2x + 4y ≤ 8
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≤ 4
Answer:
We first convert the inequalities into equations to obtain lines
2x + 4y = 8 …..(i)
3x + y = 6 …..(ii)
x + y = 4 …..(iii)
x = 0
y = 0
We need to maximise the objective function
Z = 2x + 5y
These lines are drawn and the feasible region of the L.P.P. is the shaded region.
The point of intersection of equations (i) and (ii) is B(l.6,1.2).
The coordinates of the comer points of the feasible region are 0(0,0), A(0,2), B(l.6,1.2) and C(2,0).

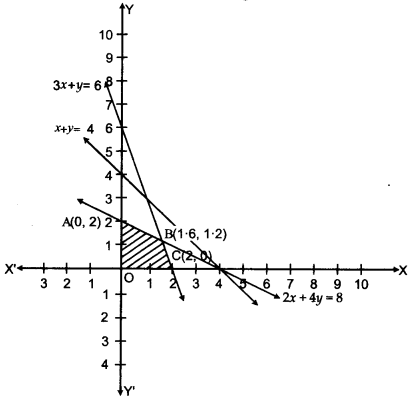
The value of the objective function at these points are given in the following table :

Comer Points	Objective function Z = 2x + 5y
0(0,0)	2 × 0 + 5 × 0 = 0
A(0, 2)	2 × 0 + 5 × 2 = 10 ← Maximum
B(T6,12)	2 × 1.6 + 5 × 1.2 = 9.2
C(2,0)	2 × 2 + 5 × 0 = 4

Out of these values of Z, the maximum value of Z is 10 which is attained at the point (0, 2). Thus the maximum value of Z is 10.

Question 28.
Evaluation : \(\int \frac{d x}{x\left(x^5+3\right)}\)
Or
Evaluation : \(\int \frac{3 x-1}{(x-1)(x-2)(x-3)} dx\)
Answer:
Let I = \(\int \frac{d x}{x\left(x^5+3\right)}\)
Multiplying num. and deno. by x⁴

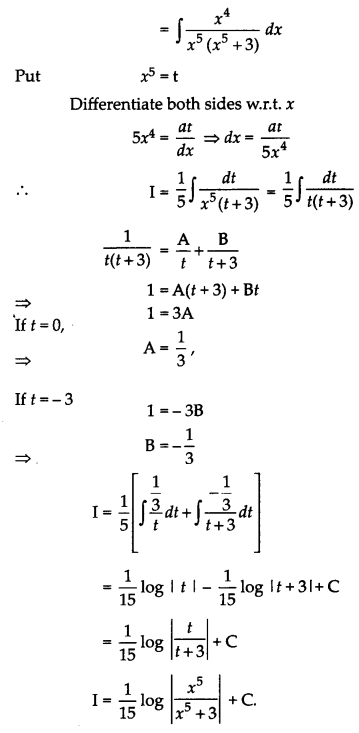
Or
\(\frac{3 x-1}{(x-1)(x-2)(x-3)}\) = \(\frac{\mathrm{A}}{x-1}+\frac{\mathrm{B}}{x-2}+\frac{\mathrm{C}}{x-3}\)
3x – 1 = A(x – 2)(x – 3) + B(x – 1)(x – 3) + C(x – 1)(x – 2)
If x = 1, then
2 = A(-1)(-2)
⇒ 2A = 2
⇒ A = 1
If x = 2, then
5 = B(1)(-1)
⇒ B = -5
If x = 3, then
8 = C(2)(1)
⇒ C = 4

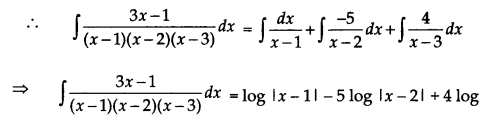
Question 29.
Solve the following differential equation :
(1 + x²) \(\frac{d y}{d x}\) + y = tan^-1 x.
Or
Solve the differential equation is,
x log x \(\frac{d y}{d x}\) + y = 2 log x
Answer:
Given differential equation is,
(1 + x²)\(\frac{d y}{d x}\) + y = tan^-1x
Divide (1 + x²) in above equation, we get
\(\frac{d y}{d x}+\frac{1}{1+x^2} y=\frac{\tan ^{-1} x}{1+x^2}\)
The above equation is of the form \(\frac{d y}{d x}\) + Py = Q
where, P = \(\frac{1}{1+x^2}\) and Q = \(\frac{\tan ^{-1} x}{1+x^2}\)

Or

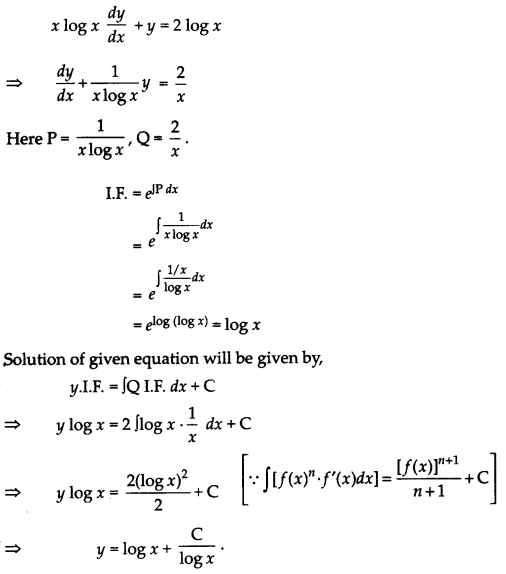
Question 30.
A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
OR
A bag contains 4 balls. Two balls are drawn at random (without replacement) and are found to be white. What is the probability that all balls in the bag are white?
Answer:
Let A be event that the sum of observations is 8.
∴ A = {(2, 6), (3, 5), (5, 3), (4, 4), (6, 2)}
⇒ n( A) = 5
⇒ P(A) = \(\frac{5}{36}\)
Let B be event that the observation on red die is less than 4.
∴ B = {(1,1), (2,1), (3,1), (4,1), (5,1), (6,1), (1,2), (2,2), (3,2), (4,2), (5,2), (6,2), (1,3), (2,3), (3,3), (4,3), (5,3), (6,3)}

Or
There are three possible cases. They are :
A₁: The bag has 2 white balls and 2 balls of other colour
A₂ : The bag has 3 white balls and 1 ball of other colour
A₃ : The bag has 4 white balls
Now, P(A₁)= P(A₂) = P(A₃) = \(\frac{1}{3}\)
Let E be the event of selecting 2 white balls.

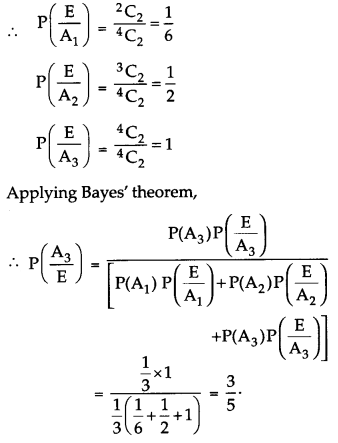
Question 31.
Find : \(\int \frac{e^x}{\left(e^x-1\right)^2\left(e^x+2\right)} dx \)
Answer:

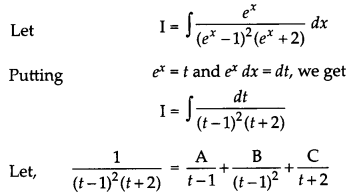
⇒ 1 = A(t – 1)(t + 2) + B(t + 2) + (t – 1)₂
Putting t = 1
⇒ 1 = 3B ⇒ B = 1/3
Putting t = -2
⇒ 1 = 9C ⇒ C = 1/9
Putting t = 0
⇒ 1 = -2A + 2B + C

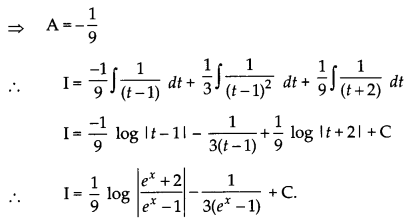
Section – D
[This section comprises of long answer-type questions (LA) of 5 marks each]

Question 32.
In a girls hostel, 60% of the student read Hindi newspaper, 40% read English newspaper and 20% read both Hindi and English newspaper. A student is selected at random.
(i) Find the probability that she reads neither Hindi nor English newspaper.
(ii) If she reads Hindi newspaper, find the probability that she reads English newspaper.
(iii) If she reads English newspaper, find the probability that she reads Hindi newspaper.
Answer:
Let H denote the event that students who read Hindi newspaper and E denote the students who read English newspaper It is given that,
P(H) = 60% = \(\frac{60}{100}=\frac{3}{5}\)
P(E) = 40% = \(\frac{40}{100}=\frac{2}{5}\)
P(H∩E) = 20% = \(\frac{20}{100}=\frac{1}{5}\)
(i) Probability that a randomly chosen student reads English newspaper if she reads a Hindi newspaper is

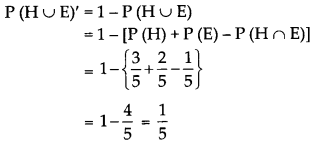
(ii) Probability that a randomly chosen student reads English newspaper if she reads a Hindi newspaper is

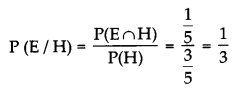
(iii) Probability that a randomly chosen student reads Hindi newspaper if she reads a English newspaper is

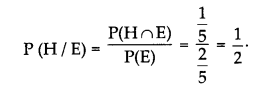
Question 33.
If S is the set of all real numbers which satisfy the function f(x) = \(\frac{2 x+1}{2 x^3+3 x^2+x}\)>0,then find all the values from the set S.
Or
Show that the relation R defined on the set A of all triangle in a plane a as R = {(T₁ : T₁ is congruent to T₂} is an equivalence relation.
Answer:
Since,

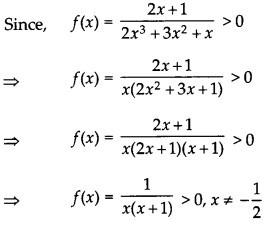
[∵ (2x + 1) cancels out in the numberator and denominator]
By using the sign rule (or otherwise) we can now find out the region on the number line where \(\frac{1}{x(1+x)}\) > 0 will be true. The region is -∞ to -1 and 0 to ∞, where neither – 1 nor 0 are included in the solution set. Hence, we write the solution as :
f(x) ∈ (-∞, -1)∪(0,∞)
Or
Given, R = {(T₁) : T₁ is congruent to T₂

Reflexivity: Let (T,T) ∈ R, ∀ T ∈ A
Since every triangle is congruent to itself i.ev R is reflexive.
Symmetric: Let (T₁, T₂) ∈ R
then, T₁ is congruent to T₂
⇒ T₂ is congruent to T₁
⇒ (T₂, T₁) ∈ R
So, R is symmetric.

Transitivity: Let T₁, T₂, T₃ ∈ A such that (T₁, T₁) ∈ R and (T₂, T₃) ∈ R. Then,
⇒ T₁ is congruent to T₂ and T₂ is congruent to T₃
⇒ T₁ is congruent to T₃
⇒ (T₁, T₃) ∈ R
So, R is transitive.
Hence, R is an equivalence relation on set A.

Question 34.
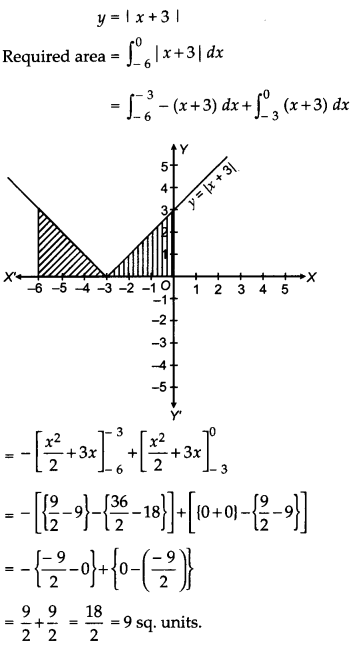
Sketch the graph of y = |x + 3| and evaluate :
and evaluate:
Answer:

Question 35.
Prove that the lines whose direction cosines are given by al + bm + cn = 0 and fmn + gnl + him = 0 are
(i) perpendicular if \(\frac{f}{a}+\frac{g}{b}+\frac{h}{c}\) = 0 and
(ii) parallel if a₂f₂ + b₂g₂ + c₂h₂ – 2(bcgh + cahf+ abfg) = 0.
OR
Find the image of the point (1, 6, 3) on the line \(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}\). Also,write the equation of the line
joining the given points and its image and find the length of segment joining given point and its image.
Answer:
Given that
al + bm + cn = 0 …..(i)
and fmn + gnl + hlm = 0 …..(ii)
form (i), al + bm = – cn
⇒ n = –\(\left(\frac{a l+b m}{c}\right)\) ……(iii)
Substituting this value of n in (ii), we get
(fm + gl)\(\left(-\frac{a l+b m}{c}\right)\) + hlm = 0
⇒ -(fm + gl)(al + bm) + hlmc = 0
⇒ -aflm – agl² – bfm² – bglm + chlm = 0
⇒ agl² + (af + bg – ch)lm + bfm² = 0
We note that both l and m cannot be zero.
For,if
l = m = 0
Then form (iii), we get n = 0
which is wrong as l² + m² + n² = 1
So, without any loss of generality we may take m ≠ 0.
Dividing both sides of (iv) by m₂, we get
\(a g\left(\frac{l}{m}\right)^2+(a f+b g-c h)\left(\frac{l}{m}\right)+b f\) = 0
The above equation is quadratic in \(\left(\frac{l}{m}\right)\)giving two value of \(\left(\frac{l}{m}\right)\)
If (l₁,m₁,n₁) and (l₂m₂,n₂) are the
direction cosines of the given lines (i)and (ii),then \(\frac{l_1}{m_1}, \frac{l_2}{m_2}\)
are roots of equation (v).
Therefore, product of root = \(\frac{b f}{a g}\)

i.e., if equation (v) has equal roots.
i.e., if discontinant of (v) is zoro.
i.e., If (af + bg – ch)₂ – 4agbf = 0
i.e., If a₂f₂ + b₂g₂ + c₂h₂ + 2abfg – 2bgch – 2afch – 4agbf = 0
i.e., a₂f₂ + b₂g₂ + c₂h₂ – 2(bcgh + cahf + abfg) = 0
Or
Here, T is the image of point P(l, 6, 3). Q is the foot of perpendicular PQ on the line AB. First, we find Q.
Equation of line AB is given by

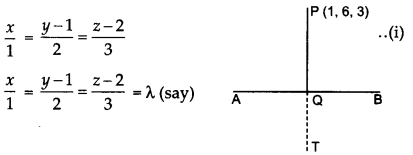
⇒ x = λ, y – 1 = 2λ, z – 2 = 3λ
⇒ x = λ, y = 2λ + 1, z – 3λ + 2
Let coordinates of
Q = (λ, 2λ + 1, 3λ + 2)
Now, direction ration of line
PQ = (λ – 1,2λ + 1 – 6, 3λ + 2 – 3)
∴ Direction ration of PQ = (λ – 1, 2λ – 5, 3λ – 1)
Now, line PQ ⊥ AB
∴ a₁a₂ + b₁b₂ + c₁c₂ = 0
Where a₁ = λ – 1, b₁ = 2λ – 5, c₁ = 3λ – 1
and a₂ = 1, b₂ = 2, c₂ = 3
∴ 1(λ – 1) + 2(2λ – 5) + 3(3λ – 1) = 0
⇒ λ – 1 + 4λ – 10 + 9λ – 3 = 0
⇒ 14λ – 14 = 0
⇒ λ = 1
Putting λ = 1 in equation (ii), we get
Q(1,2 + 1,3 + 2) = (1,3,5)
Now, as discussed earlier Q is the mid – point of PT.
Let coordinates of T = (x,y,z)
∴ Using by mid-point formula,
Q = Mid – point of P(1,6,3) and T(x,y,Z)
=\(\left(\frac{x+1}{2}, \frac{y+6}{2}, \frac{z+3}{2}\right)\)
But Q = (1,3,5)
∴ \(\left(\frac{x+1}{2}, \frac{y+6}{2}, \frac{z+3}{2}\right)\) = (1,3,5)
⇒ \(\frac{x+1}{2}=1, \frac{y+6}{2}=3, \frac{z+3}{2}\) = 5
⇒ x = 2 – 1, y = 6 – 6, z = 10 – 3
⇒ x = 1, y = 0, z = 7
∴ Coordinates of T = (x,y,z,) = (1, 0,7)
Hence, coordinates of image of point
p(1,6,3) = T(1,0,7)

Section – E
[This section comprises of 3 case-study/passage-based questions of 4 marks each with two sub-parts. The First two case study questions have three sub-parts (i), (ii), (iii) of marks 1,1, 2 respectively. The third case study question has two sub-parts of 2 marks each.]

Question 36.
A Badminton Hall is to be constructed in the form of a cube in a sports complex in the 3-D as given below:

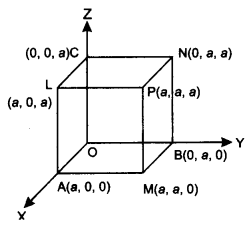
Length of side of cube be a unit four diagonals are OP, MC, AN and BL.
From the above information given answer of the following questions :
(i) Write the direction ratios of the side of the room of Z-axis.
(ii) Write the Cartesian equation of the side of the room BN.
(iii) Find the direction cosines of diagonal AN.
Or
(iii) Write the direction cosines of diagonal MC.
Answer:
(i) Direction ratios of Z-axis = (0,0, a).
(ii) Cartesian equation of side BN where B(0, a, 0), N(0, a, a) is

OR
(iii) Coordinates of diagonal MC

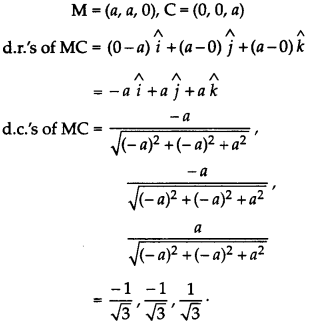
Question 37.
Two friends Raja and Rahul are standing on a point O from where they started to move in different
directions with the position vector of \(2 \hat{i}-\hat{j}+\hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}\) respectively. Raja reaches to his office at point A and Rahul reaches his client office at point B which are opposite to each other. They decided to meet at a coffee shop situated on the way of AB coffee shop divided the road AB in the ratio of 2 : 1.

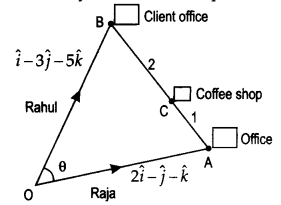
Give answers of the following questions :
(i) How much distance is covered by Raja to reach his office A’?
(ii) What is the distance between Rahul’s starting point and terminating point?
(iii) What is the distance between Raja’s office and Rahul’s client office?
Or
(iii) What are the coordinates of the point of coffee shop ?
Answer:

Question 38.
A firm produces three products P₁ P₂ and P₃ requiring the mix-up of three materials M₁, M₂ and M₃. Per unit requirement of each product for each material (in units) is represented by matrix A as follows:

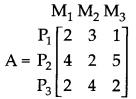
The per unit cost of material M₁, M₂ and M₃ is ₹5, ₹10 and ₹5 respectively.
(i)Find the total requirement of each material for 100 units of each product.
(ii) Find per unit cost of production of each product as per unit cost of material given above.
Answer:
The total requirement of each material is given by A’B.