CBSE Sample Papers for Class 11 Applied Mathematics Set 4 with Solutions

Students can access the CBSE Sample Papers for Class 11 Applied Mathematics with Solutions and marking scheme Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Applied Mathematics Set 4 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

• This Question paper contains five sections A, B, C, D and E. Each section is compulsory. However, there is some internal choice in some questions.
• Section A has 18 MCQs and 2 Assertion Reason-based questions of 1 mark each.
• Section B has 5 Very Short Answer (VSA) questions of 2 marks each.
• Section C has 6 Short Answer (SA) questions of 3 marks each.
• Section D has 4 Long Answer (LA) questions of 5 marks each.
• Section E has 3 source-based/case-based/passage-based/integrated units of assessment (4 marks each) with subparts.
• Internal Choice is provided in 2 questions in Section B, 2 questions in Section C, 2 Questions in Section D. You have to attempt only one alternative in all such questions.

Section-A

(All Questions are compulsory. No internal choice is provided in this section)

Question 1.
The number of ways in which a team of 11 players can be selected from 22 players always including 2 of them and excluding 4 of them is
(a) ¹⁶C₁₁
(b) ¹⁶C₅
(c) ¹⁶C₉
(d) ²⁰C₉
Answer:
(c) ¹⁶C₉
Explanation:
Total number of players = 22
Since given 2 players are always included and 4 players are always excluded or never included.
Therefore, total number of players = 22 – 2 – 4 = 16
Now, we have to choose 11 players out of which 2 are included, then we have to choose only = 11 – 2 = 9 players.
∴ Required number of selections = ¹⁶C₉

Question 2.
How many different words can be formed by using all the letters of the word ‘SCHOOL’?
(a) \(\frac{6 !}{2 !}\)
(b) 6!
(c) \(\frac{2 !}{6 !}\)
(d) None of these
Answer:
(a) \(\frac{6 !}{2 !}\)
Explanation:
Since, ‘SCHOOL’ has 6 letters, out of these 6 letters there is 2 O’s.
Hence number of permutations = \(\frac{6 !}{2 !}\)

Question 3.
If the first term of G.P. is 2 and sum to infinity is 6, then common ratio is
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{2}{3}\)
(d) None of these
Answer:
(c) \(\frac{2}{3}\)
Explanation:
Given, a = 2 and S_∞ = 6

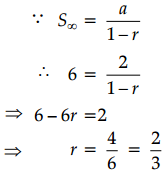
Question 4.
Which term of the sequence 3, 10, 17,……. is 136?
(a) 15th term
(b) 20th term
(c) 22th term
(d) 17th term
Answer:
(b) 20th term
Explanation:
Given sequence 3, 10, 17, ……, 136
Let n^th term be the 136,
i.e., T_n = a + (n – 1)d
⇒ 136 = 3 + (n – 1)7 [∵ a = 3 and d = 7]
⇒ 7n = 140
⇒ n = 20
Hence, 20th term of the sequence is 136.

Question 5.
If three sides of a triangle are 6 cm, 8 cm, 10 cm, then the altitude of the triangle using the largest side as base will be:
(a) 8 cm
(b) 6 cm
(c) 4.8 cm
(d) 4.4 cm
Answer:
(c) 4.8 cm
Explanation:

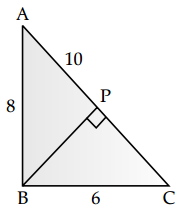
Area of ∆ABC = \(\frac{1}{2}\) × AB × BC
Also, Area of ∆ABC = \(\frac{1}{2}\) × AC × BP
∴ \(\frac{1}{2}\) × 8 × 6 = \(\frac{1}{2}\) × 10 × BP
⇒ BP = \(\frac{8 \times 6}{10}\) = 4.8 cm

Question 6.
A tyre has two punctures. The first puncture alone would have made the tyre fault in 9 minutes and second alone would have done it in 6 minutes. If air leaks out at a constant rate, then after ________ minutes both the punctures together make the tyre fault?
(a) 3\(\frac{3}{5}\) min
(b) 3\(\frac{1}{5}\) min
(c) 2\(\frac{3}{5}\) min
(d) 2\(\frac{1}{5}\) min
Answer:
(a) 3\(\frac{3}{5}\) min
Explanation:
1 minute’s work of both the punctures = \(\frac{1}{9}+\frac{1}{6}=\frac{5}{18}\)
So, both the punctures will make the tyre flat in = \(\frac{18}{5}\) = 3\(\frac{3}{5}\) min

Question 7.
Today is Monday, then what is the day after 61 days?
(a) Monday
(b) Wednesday
(c) Friday
(d) Saturday
Answer:
(d) Saturday
Explanation:
Each day of the week is repeated after 7 days. So, after 63 Days, it will be Monday.

Question 8.
The average of first nine prime numbers is
(a) \(\frac{77}{9}\)
(b) \(\frac{101}{9}\)
(c) \(\frac{58}{9}\)
(d) \(\frac{100}{9}\)
Answer:
(d) \(\frac{100}{9}\)
Explanation:
First nine prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23
∴ Average = \(\frac{2+3+5+7+11+13+17+19+23}{9}\) = \(\frac{100}{9}\)

Question 9.
Which is most appropriate to complete the sentence ‘A newspaper always has ________’.
(a) Date
(b) Editor
(c) News
(d) Paper
Answer:
(c) News
Explanation:
All the given words are relevant for a newspaper, but out of these the word ‘News’ is most appropriate and remaining are removed. So, the given sentence can be completed as ‘A newspaper always has news’.

Question 10.
The domain of f(x) = x|x|
(a) R⁺
(b) R^–
(c) R
(d) None of these
Answer:
(c) R
Explanation:
Given, f(x) = x|x|
Here, f(x) is defined for any x ∈ R
∴ Domain of f = R

Question 11.
Derivative of x^x w.r.t. x is
(a) x^x (1 – log x)
(b) x^x (log x – 1)
(c) x^x (2 + log x)
(d) x^x (1 + log x)
Answer:
(d) x^x (1 + log x)
Explanation:
y² = x^x
taking logarithm of both sides
log y = log x^x = x log x
\(\frac{d y}{d x} \log y=\frac{d}{d x}(x \log x)\)

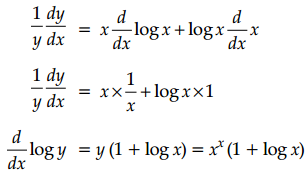
Question 12.
Let A and B be two given mutually exclusive events. Then P(\(\frac{A}{B}\)) is
(a) 1
(b) 0
(c) P(A)
(d) P(B)
Answer:
(b) 0
Explanation:
P(A ∩ B) = 0 [∵ A and B are mutually exclusive events]
∴ \(P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}=\frac{0}{P(B)}\) = 0

Question 13.
When the frequency curve is more peaked than normal curve it is called
(a) Leptokurtic
(b) Mesokurtic
(c) Platykurtic
(d) None of these
Answer:
(a) Leptokurtic
Explanation:
The curves with greater peakness than the normal curve are called leptokurtic.

Question 14.
For the data: 5, 24, 36, 12, 20, and 8, value of D₅ is
(a) 24
(b) 20
(c) 16
(d) 12
Answer:
(c) 16
Explanation:
Arranging the given data in ascending order, we get
5, 8, 12, 20, 24, 36
D₅ = \(\frac{5(6+1)}{10}^{\text {th }}\) value
= 3.5th value
= 3rd value + \(\frac{1}{2}\)(4th value – 3rd value)
= 12 + \(\frac{1}{2}\)(20 – 12)
= 12 + 4
= 16

Question 15.
Sachin deposited ₹ 100000 in his bank for 2 years at simple rate of 6%. How much interest would he earn? The final value of his deposit will be
(a) ₹ 112000
(b) ₹ 102000
(c) ₹ 112200
(d) ₹ 112020
Answer:
(a) ₹ 112000
Explanation:
Required interest amount is given by
I = Pit
= 100000 × \(\frac{6}{100}\) × 2
= ₹ 12,000
Final value of deposit is given by
A = P + I
= ₹ (100000 + 12000)
= ₹ 112000

Question 16.
The effective annual rate of interest corresponding to a nominal rate of 7% per annum payable half-yearly is
(a) 7.02%
(b) 7.12%
(c) 7.0%
(d) 7.25%
Answer:
(b) 7.12%
Explanation:
∵ Effective rate, E = (1 + i)ⁿ – 1
Here, i is 7% half yearly = \(\frac{7}{100} \times \frac{1}{2}\)
n = 2
∴ E = \(\left(1+\frac{7}{100} \times \frac{1}{2}\right)^2\) – 1
= (1 + 0.035)² – 1
= (1.035)² – 1
= 1.0712 – 1
= 0.0712
= 7.12%
The effective interest rate is 7.12%.

Question 17.
Taxes that are levied on any Intra-State purchase are?
(a) IGST
(b) CGST and SGST
(c) SGST
(d) None of these
Answer:
(b) CGST and SGST

Question 18.
The point on X-axis, whose distance from the line \(\frac{x}{3}+\frac{y}{4}\) = 1 is 4 units is
(a) (8, 0) or (-2, 0)
(b) (-8, 0) or (2, 0)
(c) (-8, 0) or (-2, 0)
(d) None of these
Answer:
(a) (8, 0) or (-2, 0)
Explanation:
The given line is \(\frac{x}{3}+\frac{y}{4}\) = 1
⇒ 4x + 3y = 12
⇒ 4x + 3y – 12 = 0 ……(i)
Any point on X-axis is P(x, 0).
So, the distance of P(x, 0) from line (i) is
4 = \(\frac{|4 . x+3.0-12|}{\sqrt{4^2+3^2}}\)
⇒ 4 = \(\frac{|4 x-12|}{\sqrt{25}}\)
⇒ |4x – 12| = 20
⇒ 4x – 12 = ±20
Either 4x – 12 = 20 or 4x – 12 = -20
4x = 32 or 4x = -8
Thus x = 8 or x = -2
Required points are (8, 0) or (-2, 0).

Direction (Q.19 & Q.20): In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.

Question 19.
Observe the given data:

x	10-15	15-20	20-25	25-30
frequency	4	10	16	8

Assertion (A): The range of given data is 20.
Reason (R): The coefficient of range of given data is 50.
Answer:
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
Explanation:
Here, lower class limit of the first class interval, S = 10
and upper class limit of the last class interval, L = 30
∴ Range = L – S
= 30 – 10
= 20
Coefficient of range = \(\frac{L-S}{L+S}\) × 100
= \(\frac{30-10}{30+10}\) × 100
= \(\frac{20}{40}\) × 100
= 50

Question 20.
Assertion (A): Decimal convergent of (25)₁₀ is (11001)₂.
Reason (R): Decimal convergent of (25)₁₀ is (10011)₂.
Answer:
(c) (A) is true but (R) is false.
Explanation:
Divide the decimal number 25 by 2.

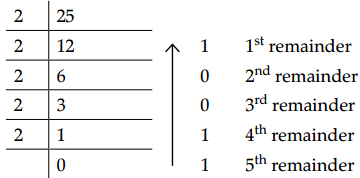
Collect the remainder from the bottom to top to get binary equivalent.
∴ (25)₁₀ = (11001)₂

Section-B

(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 21.
What do you understand by the terms electricity tariff and fuel surcharge?
Answer:
Electricity Tariff:
The amount of money frame by the supplier for the supply of electrical energy to various types of consumers is known as an electricity tariff. In other words, the tariff is the methods of charging a consumer for consuming electric power.

Fuel Surcharge:
It is a charge that is applicable per unit of electricity consumed. Unlike fixed charges, it is a variable component on the electricity bill and changes as per your consumption of electricity every month.

Question 22.
A person invests ₹ 500 at the end of each year with a bank which pays interest at 10% p.a. C.I. annually. Find the amount standing to his credit one year after he has made his yearly investment for the 12th time. [Given that (1.1)¹² = 3.1348]
Answer:

Amount after one year i.e., after 12th installment = F.V × (1 + i)
= 10692.14 × (1.1)
= ₹ 11761

Question 23.
Find the variance of first n natural numbers.
OR
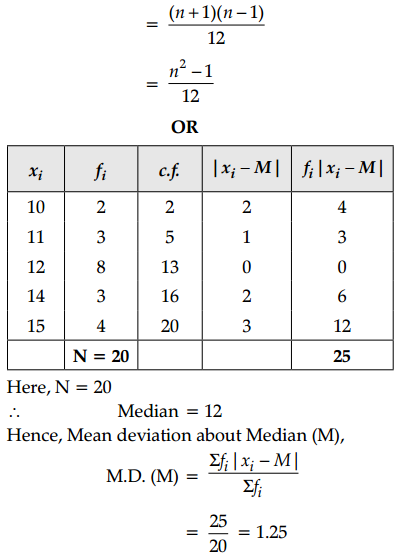
Find the mean deviation about the median of the following distribution.

Marks Obtained	10	11	12	14	15
No. of Students	2	3	8	3	4

Answer:
Here, the variables are 1, 2, 3,…….,n

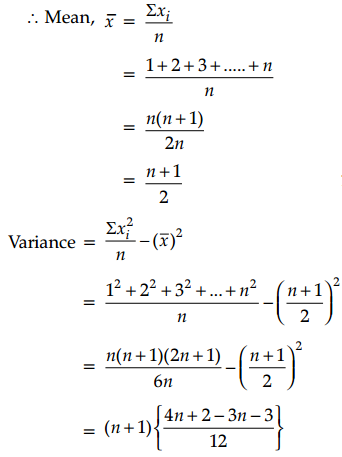
Question 24.
Two dice are thrown. If it is known that the sum of numbers on the die was less than 6, then find the probability of getting a sum of 3.
OR
A company has estimated the probabilities of success for three products introduced in the market are \(\frac{1}{3}\), \(\frac{2}{5}\) and \(\frac{2}{3}\), respectively. Assuming independence, find the probability that the three products are successful.
Answer:
Let, E₁ = Event that the sum of numbers on the dice was less than 6
and E₂ = Event that the sum of numbers on the dice is 3.
∴ E₁ = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}
⇒ n(E₁) = 10
and E₂ = {(1, 2), (2, 1)}
⇒ n(E₂) = 2
∴ Required Probability = \(\frac{n\left(E_2\right)}{n\left(E_1\right)}=\frac{2}{10}\)
OR
Let A = First product is successful
B = Second product is successful
C = Third product is successful
We have, P(A) = \(\frac{1}{3}\), P(B) = \(\frac{2}{5}\) and P(C) = \(\frac{2}{3}\)
P(All three products are successful) = P(A ∩ B ∩ C) = P(A).P(B).P(C)
[∵ Given A, B and C are independent events]
= \(\frac{1}{3} \times \frac{2}{5} \times \frac{2}{3}\)
= \(\frac{4}{45}\)

Question 25.
If A is the son of P, B is P’s sister, B has a son Q and a daughter C, R is the maternal uncle of Q, then answer the following questions.
(i) How many nephews does R have?
(ii) How many brothers does B have?
Answer:
First we have to draw the family chart from the given relationship.

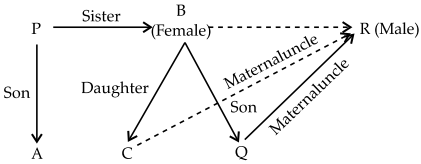
From the above chart, we see that P has only one son.
A, B is the only sister of P and R also, B has one son (Q) and one daughter (C).
So, R and P are the maternal uncle of Q and C.
(i) R has two nephews, A and Q.
(ii) B has two brothers, P and R.

Section – C

(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 26.
For an industrial connection monthly consumption of water is 40 kl, calculate the Water bill. Tariff rates can be considered the table given below:

Monthly Consumption (in kilolitre)	Service Charge (in ₹)	Volumetric Charge (Per kl in ₹)
Upto 20	146.41	5.27
20-30	219.62	26.36
>30	292.82	43.93

Plus Sewer Maintenance Charge: 60% of water volumetric charge
Answer:
Volumetric Charge for consumption upto 20 kl = ₹ 20 × 5.27 = ₹ 105.4
Volumetric Charge for consumption between 20-30 kl = ₹ 10 × 26.36 = ₹ 263.6
Volumetric Charge for consumption between 30-40 kl = ₹ 10 × 43.93 = ₹ 439.3
Total volumetric Charge for consumption of 40 kl = ₹ (105.4 + 263.6 + 439.3) = ₹ 808.3
Service Charge = ₹ 292.82
Sewage Charges = 60% of Volumetric Charges
= 808.3 × 60%
= ₹ 484.98
Amount of water bill for the given month = ₹ (808.3 + 292.82 + 484.98) = ₹ 1586.1
Thus, amount of domestic water bill is ₹ 1586.

Question 27.
The first four raw moments of a distribution are 2, 136, 320 and 40000. Find out coefficient of skewness.
OR
For a group of 60 boys students, the mean and S.D. of statistics marks are 45 and 2 respectively. The same figures for a group of 40 girls students are 55 and 3 respectively. What is the mean and S.D. of marks if the two groups are pooled together?
Answer:
Given that, \(\mu_1^{\prime}\) = 2, \(\mu_2^{\prime}\) = 136, \(\mu_3^{\prime}\) = 320 and \(\mu_4^{\prime}\) = 40000
First of all we have to calculate the first four central moments

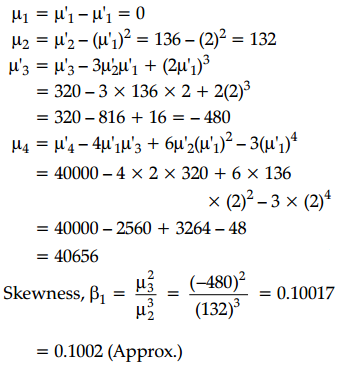
Question 28.
Draw the graph of the function f(x) = \(\begin{cases}1+2 x, & x<0 \\ 3+5 x, & x \geq 0\end{cases}\). Also, find its range.
OR
Let A = {9, 10, 11, 12, 13} and let f: A → N defined by f(n) = the highest prime factor of n. Find the range of f.
Answer:
Given, f(x) = \(\begin{cases}1+2 x, & x<0 \\ 3+5 x, & x \geq 0\end{cases}\)
Here, f(x) = 1 + 2x, x < 0, this gives
f(-4) = 1 + 2(-4) = -7
f(-3) = 1 + 2(-3) = -5
f(-2) = 1 + 2(-2) = -3
f(-1) = 1 + 2(-1) = -1
and f(x) = 3 + 5x, x ≥ 0
f(0) = 3 + 5(0) = 3
f(1) = 3 + 5(1) = 8
f(2) = 3 + 5(2) = 13
f(3) = 3 + 5(3) = 18
f(4) = 3 + 5(4) = 23
Now the graph of f is as shown in the following figure.

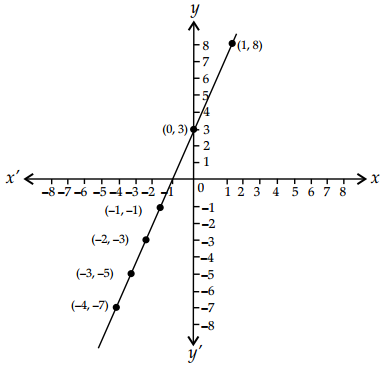
Range: Let y₁ = f(x), x < 0
⇒ y₁ = 1 + 2x, x < 0
⇒ x = \(\frac{y_1-1}{2}\), x < 0
∵ x < 0
⇒ y₁ – 1 < 0
⇒ y₁ < 1
Let y₂ = f(x), x ≥ 0
⇒ y₂ = 3 + 5x, x ≥ 0
⇒ x = \(\frac{y_2-3}{5}\), x ≥ 0
∵ x ≥ 0
⇒ y₂ – 3 ≥ 0
⇒ y₂ ≥ 3
Therefore, range of f (-∞, 1) ∪ [3, ∞).
OR
Given, A = {9, 10, 11, 12, 13} and f : A → N
and f(n) = the highest prime factor of ‘n’
For n = 9, 9 = 1 × 3 × 3
⇒ Highest prime factor of 9 = 3
For n = 10, 10 = 1 × 2 × 5
⇒ Highest prime factor of 10 = 5
For n = 11, 11 = 1 × 11
⇒ Highest prime factor of 11 = 11
For n = 12, 12 = 1 × 2 × 2 × 3
⇒ Highest prime factor of 12 = 3
For n = 13, 13 = 1 × 13
⇒ Highest prime factor of 13 = 13
∴ f(n) = {(9, 3), (10, 5), (11, 11), (12, 3), (13, 13)}
⇒ Range = {3, 5, 11, 13}

Question 29.
In each question below are two statements followed by two conclusions numbered I and II. You have to take the two given statements to be variance from commonly known facts and decide which of the given conclusions logically follows the two given statements disregarding commonly known facts.
Give answer:
(a) if only conclusion I follow
(b) if only conclusion II follows
(c) if either I or II follows
(d) if neither I nor II follows
(e) if both I and II follow
(i) Statements: (i) All stones are water.
(ii) Some waters are clean.
Conclusions: I. Some stones are clean.
II. No stone is clean.
(ii) Statements: (i) All keys are locks.
(ii) All locks are screws.
Conclusions: I. All screws are keys.
II. Some locks are keys.
Answer:
(i) Conclusion I and II are mediate inference since the middle term is not distributed no conclusion follows. But both conclusions form a complimentary pair.
Hence, either I or II follows i.e., option (c).

(ii) Conclusion II follows being the converted form of the statement (i). Conclusion I is mediate inference and does not follow as the term screws are not distributed in the statement.
Hence, only conclusion II follows i.e., option (b).

Question 30.
If a, b, c are in A.P. show that \(a\left(\frac{1}{b}+\frac{1}{c}\right), b\left(\frac{1}{c}+\frac{1}{a}\right), c\left(\frac{1}{a}+\frac{1}{b}\right)\) are also in A.P.
Answer:

Question 31.
If x = \(a+\frac{a}{r}+\frac{a}{r^2}+\ldots+\infty\), y = \(b-\frac{b}{r}+\frac{b}{r^2}+\ldots+\infty\) and z = \(c+\frac{c}{r^2}+\frac{c}{r^4}+\ldots+\infty\), Prove that \(\frac{x \cdot y}{z}=\frac{a b}{c}\)
Answer:
Given series x = \(a+\frac{a}{r}+\frac{a}{r^2}+\ldots+\infty\) is in G.P with common ratio \(\frac{1}{r}\).
and series y = \(b-\frac{b}{r}+\frac{b}{r^2}+\ldots+\infty\) is in G.P with common ratio \(-\frac{1}{r}\).
and series z = \(c+\frac{c}{r^2}+\frac{c}{r^4}+\ldots+\infty\) is in G.P with common ratio \(\frac{1}{r^2}\).
Sum of infinite terms of series


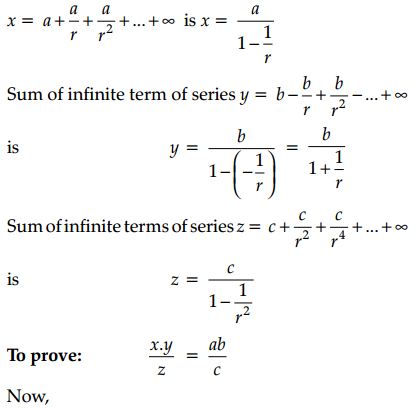
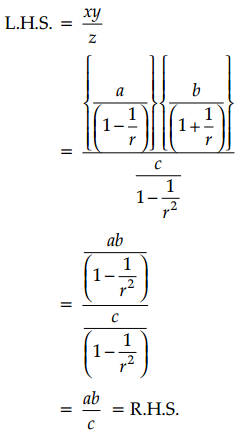
Hence Proved.

Section-D

(This section comprises long answer type questions (LA) of 5 marks each)

Question 32.
Manjeet, Dilawar and Ravi live in the same city. Manjeet sells an article to Dilawar for ₹ 60,000 and Dilawar sells the same article to Ravi at a profit of ₹ 8,000. If all the transactions are under GST system at the rate of 12%, find:
(i) The state-government tax (SGST) paid by Dilawar.
(ii) The total tax received by CGST.
(iii) How much does Ravi pay for the article?
Answer:
Given the rate of GST = 12%
∴ CGST rate = SGST rate = 6%
(i) Tax paid by Dilawar to SGST = SGST received by Dilawar on selling price – SGST paid by him on purchasing
= \(\frac{6}{100}\) × (60,000 + 8,000) – \(\frac{6}{100}\) × 60,000
= \(\frac{6}{100}\) × 68,000 – \(\frac{6}{100}\) × 60,000
= \(\frac{6}{100}\) × (68,000 – 60,000)
= \(\frac{6}{100}\) × 8,000
= ₹ 480

(ii) Total Tax received by CGST = CGST paid by Manjeet + CGST paid by Dilawar
= \(\frac{6}{100}\) × 60,000 + ₹ 480
= ₹ (3600 + 480)
= ₹ 4080

(iii) The amount, Ravi paid for the article = Cost price of the article for Ravi with GST
= ₹(68000 + \(\frac{12}{100}\) × 68000)
= ₹(68000 + 8160)
= ₹ 76160

Question 33.
A bag contains 8 red and 5 white balls. Two successive draws of all 3 balls are made at random from the bag without replacements. Find the probability that the first draw yields 3 white balls and second draw yields 3 red balls.
OR
A fair coin is tossed four times, and a person win ₹ 1 for each head and lose ₹ 1.50 for each tail that turns up. From the sample space calculate how many different amounts of money you can have after four tosses and the probability of having each of these amounts.
Answer:
Let E: Event that 3 balls in the first draw are all white.
F: Event that 3 balls in the second draw are all red.
Now, 3 balls can be drawn out of 13 in ¹³C₃ ways and 3 white balls can be drawn out of 5 in ⁵C₃ ways.
P(E) = \(\frac{{ }^5 C_3}{{ }^{13} C_3}=\frac{5 !}{3 ! \times 2 !} \times \frac{3 ! \times 10 !}{13 !}=\frac{5}{143}\)
Since 3 balls are not replaced before the second draw, we are left with 8 red and 2 white balls.
Now, 3 balls can be drawn in ¹⁰C₃ ways and 3 red balls can be drawn in ⁸C₃ ways.

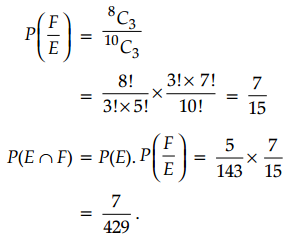
OR
(i) When no head and 4 tails appear.
Let A be the event money lost = ₹(4 × 1.50) = ₹ 6
There is only one way of getting no head and 4 tails i.e., (TTTT)
⇒ n(A) = 1
n(S) = 16, since there are 16 possible outcomes
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{1}{16}\)

(ii) Let B be the event when 1 head and 3 tails appear.
∴ B = {HTTT, THTT, TTHT, TTTH}
⇒ n(B) = 4
Money lost = ₹(3 × 1.50 – 1 × 1) = ₹ 3.50
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{4}{16}=\frac{1}{4}\)

(iii) Let C be the event that 2 head and 2 tail appear.
∴ Money lost = ₹(2 × 1.50 – 2 × 1) = ₹ 1
C = {HHTT, HTHT, HTTH, THHT, THTH, TTHH}
⇒ n(C) = 6
∴ P(C) = \(\frac{n(C)}{n(S)}=\frac{6}{16}=\frac{3}{8}\)

(iv) Let D be the event that 3 head and 1 tail appear.
∴ D = {HHHT, HHHT, THHH, HHTH}
⇒ n(D) = 4
Money gained = ₹(3 × 1 – 1 × 1.5) = ₹ 1.50
∴ P(D) = \(\frac{n(D)}{n(S)}=\frac{4}{16}=\frac{1}{4}\)

(v) Let E be the event that all heads appear.
∴ E = {HHHH}
⇒ n(E) = 1
Money gained = ₹(4 × 1) = ₹ 4
Also, P(E) = \(\frac{n(E)}{n(S)}=\frac{1}{16}\)

Question 34.
y = \(\sqrt{1+\sqrt{\left(1+x^4\right)}}\) prove that: y(y2 – 1)\(\frac{d y}{d x}\) = x³.
Answer:

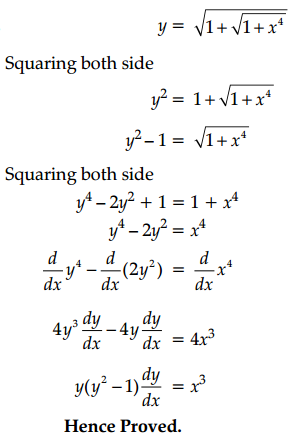
Question 35.
If ⁿC_r-1 = 36, ⁿC_r = 84, and ⁿC_r+1 = 126, then find the value of ^rC₂.
OR
Find the number of words with or without meaning which can be made using all the letters of the word AGAIN. If these words are written as in dictionary, what will be the 50th word?
Answer:


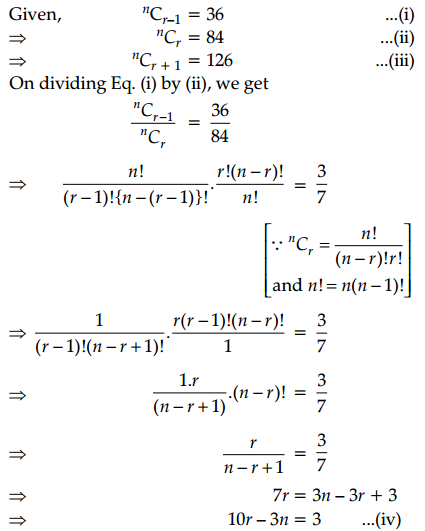
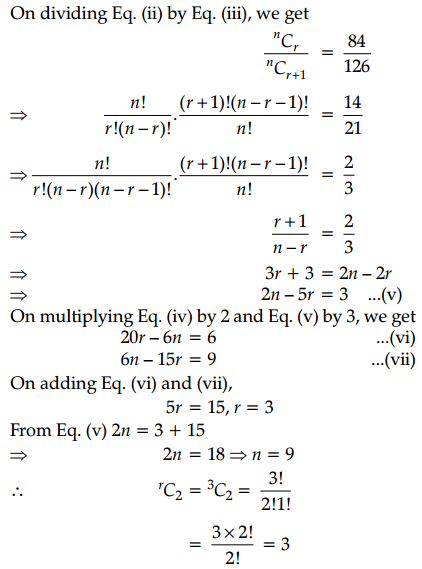
OR
Number of words made from letters of word AGAIN = \(\frac{5!}{2!}\) = 60
To get the number of words starting with A, we fix the letter A at the extreme left position, we then rearrange the remaining 4 letters taken all at a time.
There will be as many arrangements of these 4 letters taken 4 at a time as there are permutation of 4 different things taken 4 at a time.
Hence, the number of words starting with A = 4! = 24
Then, starting with G, the number of words 4! = \(\frac{4!}{2!}\) = 12.
As after placing G at the extreme left position, we are left with the letters, A, A, I and N.
Similarly, there are 12 words starting with the next letter I.
Total number of words so far obtained = 24 + 12 + 12 = 48
The 49th word is NAAGI.
The 50th word is NAAIG.

Section – E

(This section comprises 3 source-based questions (Case Studies) of 4 marks each)

Question 36.
A group of students were discussing logarithm properties as the exams were approaching. They prepared notes on base changing properties on logarithm for quick revision before examination.


On the basis of this information answer the following questions:
(i) Find the value of log2 8.
OR
Find the value of \(\log _{2^3} 16^9\).
(ii) \(\frac{\log 27 \times \log 16 \times \log 125}{\log 3 \times \log 2 \times \log 5}=\alpha\), then find the value of α.
(iii) If log_a bc = x, log_b ca = y, logc _a ab = z, then find the value of \(\frac{1}{x+1}+\frac{1}{y+1}=\frac{1}{z+1}\)
Answer:

Question 37.
In XI standard, teacher was discussing about Spearman’s Rank Correlation Coefficient in Statistics. Following points were discussed in the class about the same topic:

When we are finding correlation between two qualitative characteristics, say, beauty and intelligence, we take recourse to using rank correlation coefficient. Rank correlation can also be applied to find the level of agreement (or disagreement) between two judges so far as assessing a qualitative characteristic is concerned. As compared to product moment correlation coefficient, rank correlation is easier to compute, it can also be advocated to get a first hand impression about the correlation between a pair of variables.
Spearman’s rank correlation coefficient is given by rs _s = 1 – \(\frac{6 \Sigma d^2}{n\left(n^2-1\right)}\)
where,
d = difference between ranks of corresponding x and y
n = number of pairs of values (x, y) in the data
For example:
Ranks obtained by 10 students are given below:

Rank in Math (Rx)	10	5	6	1	2	3	4	7	8	9
Rank in Physics (Ry)	5	6	9	2	8	7	3	4	10	1

On the basis of this concept, students were given the following problem:
(i) What is the value of n2 in the given data?
(ii) Find the value of Σd and Σd2².
OR
What is rank correlation of the given data?
(iii) What does very low value of the rank correlation indicates?
Answer:
(i) n2 ² = 10² = 100


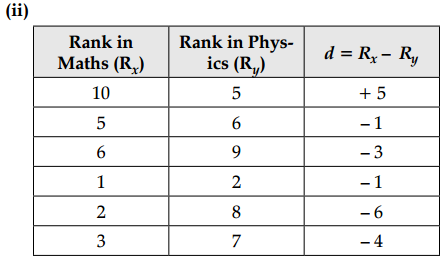
(iii) The very low value (almost 0) indicates that there is hardly any agreement between the ranks.

Question 38.
A parabola is the locus of a point which moves in a plane such that its distance from a fixed point is always equal to its distance from a straight line in the same.

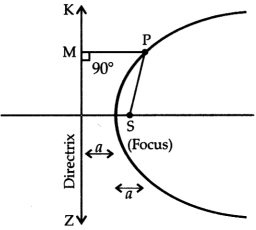
Here, the fixed point ‘P’ is called the focus and the fixed straight line is called the directrix of the parabola. The line through the focus and perpendicular to the directrix is the axis of parabola. The point on the axis midway between focus and directrix is called the vertex of the parabola. Let S be the focus and ZK be the directrix and let P be any point on the parabola. Then, by definition
\(\frac{SP}{PM}\) = e = 1
⇒ SP = PM
where PM is the length of perpendicular from P on the directrix ZK.
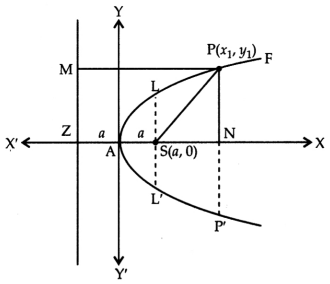
The standard equation of parabola is y2 = 4ax

For the parabola y² = 4ax,
(i) Coordinates of vertex, A are (0, 0)
(ii) Coordinates of focus, S are (a, 0)
(iii) Equation of directrix, ZM is x = -a i.e., x + a = 0
(iv) Equation of axis, ZX is y = 0 (i.e., X-axis)
(v) Equation of tangent (YY’) on the vertex is x = 0 (i.e., Y-axis)
(i) An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?
OR
(ii) Find the vertex, focus, axis, directrix, latus-rectum of parabola 4y² + 12x – 20y + 67 = 0.
Answer:
(i) The origin of the coordinate plane is taken at the vertex of the arch in such a way that its vertical axis is along the positive-axis. This can be diagrammatically represented as:

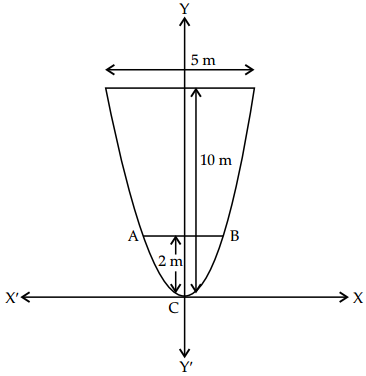
The equation of the parabola is of the form x² = 4ay (as it is opening upwards).
It can be clearly seen that the parabola passes through point (\(\frac{5}{2}\), 10).
\(\left(\frac{5}{2}\right)^2\) = 4a(10)
⇒ a = \(\frac{25}{4 \times 4 \times 10}=\frac{5}{32}\)
Therefore, the arch is in the form of a parabola whose equation is, x² = \(\frac{5}{8}\)y.
When y = 2 m, x² = \(\frac{5}{8}\) × 2
⇒ x² = \(\frac{5}{4}\)
⇒ x = \(\sqrt{\frac{5}{4}}\) m
∴ AB = 2 × \(\sqrt{\frac{5}{4}}\) m
⇒ AB = 2 × 1.11 m (approx.)
⇒ AB = 2.23 m (approx.)
Hence, when the arch is 2 m from the vertex of the parabola, its width is approximately 2.23 m.
OR
(ii) The given equation of parabola is 4y² + 12x – 20y + 67 = 0
⇒ y² + 3x – 5y + \(\frac{67}{4}\) = 0

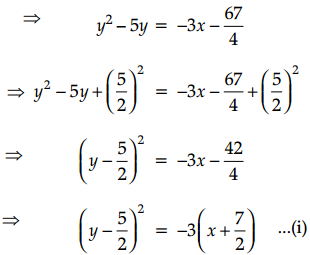
Shifting the origin to the point \(\left(\frac{-7}{2}, \frac{5}{2}\right)\) without rotating the axes and denoting the new conditions w.r.t. these axes by X and Y, we have
x = X – \(\frac{7}{2}\)
and y = Y + \(\frac{5}{2}\) …….(ii)
using these relations, equation (i) reduces to
Y² = -3X ……(iii)
This is of the form Y² = -4ax. On comparing, we get
4a = 3
⇒ a = \(\frac{3}{4}\)

Vertex: The coordinates of the vertex with respect to the new axes are (X = 0, Y = 0).
So, the coordinates of vertex with the respect to the old axes are \(\left(\frac{-7}{2}, \frac{5}{2}\right)\) [Putting X = 0, Y = 0 in equation (ii)]

Axis: The equation of the axis of parabola with respect to the new axis is Y = 0. So, the equation of the axis w.r.t. the old axes is y = \(\frac{5}{2}\) [Putting Y = 0 in equation (ii)]

Focus: The coordinates of the focus w.r.t. the new axes are (X = -a, Y = 0) i.e., (X = \(-\frac{3}{4}\), Y = 0).
So, the coordinates of the focus w.r.t. the old axes are \(\left(\frac{-17}{4}, \frac{5}{2}\right)\) [Putting X = \(-\frac{3}{4}\) and Y = 0 in equation (ii)]

Directrix: The equation of the directrix with respect to the new axis is X = a i.e., X = \(\frac{3}{4}\). So, the equation of the directrix w.r.t. the old axes is x = \(-\frac{11}{2}\) [Putting X = \(\frac{3}{4}\) in equation (ii)]

Latus-rectum: The length of the latus-rectum of the given parabola is 4a = 3.