CBSE Sample Papers for Class 11 Applied Mathematics Set 1 with Solutions

Students can access the CBSE Sample Papers for Class 11 Applied Mathematics with Solutions and marking scheme Set 1 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Applied Mathematics Set 1 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

• This Question paper contains five sections A, B, C, D and E. Each section is compulsory. However, there is some internal choice in some questions.
• Section A has 18 MCQs and 2 Assertion Reason based questions of 1 mark each.
• Section B has 5 Very Short Answer (VSA) questions of 2 marks each.
• Section C has 6 Short Answer (SA) questions of 3 marks each.
• Section D has 4 Long Answer (LA) questions of 5 marks each.
• Section E has 3 source-based/case-based/passage-based/integrated units of assessment (4 marks each) with subparts.
• Internal Choice is provided in 2 questions in Section B, 2 questions in Section C, 2 Questions in Section D. You have to attempt only one alternative in all such questions.

Section-A

(All Questions are compulsory. No internal choice is provided in this section)

Question 1.
Which of the following is not a binary number?
(a) 1111
(b) 101
(c) 11E
(d) 000
Answer:
(c) 11E
Explanation:
A binary number can have only two possible digits 0 and 1. In third option, there is an alphabet E present which makes it invalid binary number. Alphabets are only allowed in the hexadecimal number system.

Question 2.
The average of first five multiples of 3 is
(a) 3
(b) 9
(c) 12
(d) 15
Answer:
(b) 9
Explanation:
The five multiples of 3 are 3, 6, 9, 12, 15.
∴ Average = \(\frac{3+6+9+12+15}{5}=\frac{45}{5}\) = 9

Question 3.
On 8th Dec, 2007 Saturday falls. What day of the week was it on 8th Dec, 2006?
(a) Sunday
(b) Thursday
(c) Tuesday
(d) Friday
Answer:
(d) Friday
Explanation:
The year 2006 is an ordinary year. So, it has 1 odd day.
So, the day on 8th Dec, 2007 will be 1 day beyond the day on 8 Dec, 2006.
But, 8th Dec, 2007 is Saturday.
∴ 8th Dec, 2006 is Friday.

Question 4.
In a G.P. of even number of terms, the sum of all terms is 5 times the sum of the odd terms. The common ratio of the G.P. is
(a) \(-\frac{4}{5}\)
(b) \(\frac{1}{5}\)
(c) 4
(d) None of these
Answer:
(c) 4
Explanation:
Let us consider a G.P. a, ar, ar², …… with 2n terms.
We have, \(\frac{a\left(r^{2 n}-1\right)}{r-1}=\frac{5 a\left[\left(r^2\right)^n-1\right]}{r^2-1}\)
(Since common ratio of odd terms will be r² and number of terms will be n)
\(\frac{a\left(r^{2 n}-1\right)}{(r-1)}=5 \frac{a\left(r^{2 n}-1\right)}{\left(r^2-1\right)}\)
⇒ a(r + 1) = 5a
⇒ r = 4

Question 5.
In an examination there are three multiple choice questions and each question has 4 choices. Number of ways in which a student can fail to get all answer correct is
(a) 11
(b) 12
(c) 27
(d) 63
Answer:
(d) 63
Explanation:
There are three multiple choice questions, each has four possible answers. Therefore, the total number of possible answers will be 4 × 4 × 4 = 64.
Out of these possible answers only one will be correct and hence number of ways in which a student can fail to get correct answer is 64 – 1 = 63.

Question 6.
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is _________
(a) 18
(b) 15
(c) 12
(d) 6
Answer:
(a) 18
Explanation:
We know that, to form a parallelogram, we need a pair of lines from the set of 4 lines and another pair of lines from another set of 3 lines.
Therefore, required number of parallelogram = ⁴C₂ × ³C₂ = 6 × 3 = 18

Question 7.
Showing a lady in the park, Vineet said, “She is the daughter of my grandfather’s only son.” How is Vineet related to that lady?
(a) Brother
(b) Cousin
(c) Father
(d) Uncle
Answer:
(a) Brother
Explanation:
The only son of Vineet’s grandfather is the father of Vineet and Daughter of Vineet’s father is the sister of Vineet. Hence, Vineet is the brother of the lady.

Question 8.
If f(x) = ax + b, where a and b are integers, f(-1) = -5 and f(3) = 3, then a and b are equal to
(a) a = -3, b = -1
(b) a = 2, b = -3
(c) a = 0, b = 2
(d) a = 2, b = 3
Answer:
(b) a = 2, b = -3
Explanation:
We have, f(x) = ax + b
⇒ f(-1) = a(-1) + b
⇒ -5 = -a + b ……….(i)
Also, f(3) = a(3) + b
⇒ 3 = 3a + b ……(ii)
On solving equations (i) and (ii), we get a = 2, b = -3.

Question 9.
Which of the following graph is continuous?




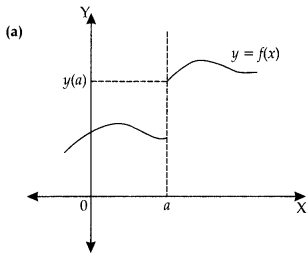
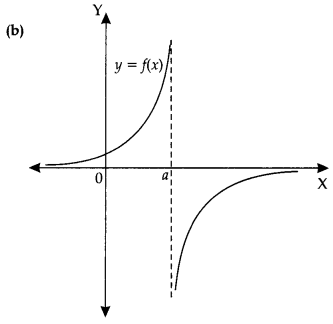
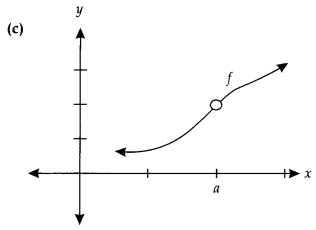
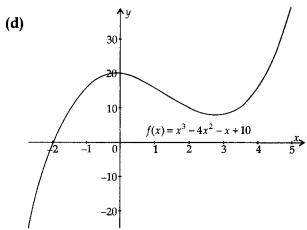
Answer:

Explanation:
Except graph (d) all the graphs has discontinuities.

Question 10.
If e₁, e₂, e₃, and e₄ are the four elementary outcomes in a sample space and P(e₁) = 0.1, P(e₂) = 0.5 and P(e₃) = 0.1, then the probability of e₄ is _________
(a) 0.1
(b) 0.3
(c) 0.5
(d) none of these
Answer:
(b) 0.3
Explanation:
We know that the sum of all probabilities = 1
∴ P(e₁) + P(e₂) + P(e₃) + P(e₄) = 1
⇒ 0.1 + 0.5 + 0.1 + P(e₄) = 1
⇒ P(e₄) = 1 – (0.7)
⇒ P(e₄) = 0.3

Question 11.
A die is thrown and a card is selected at random from a deck of 52 playing cards. The probability of getting an even number on the die and a spade card is _________
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{8}\)
(d) none of these
Answer:
(c) \(\frac{1}{8}\)
Explanation:
Let E₁ = Getting an even number on the die
E₂ = A card selected is a spade card
∴ P(E₁) = \(\frac{3}{6}=\frac{1}{2}\) and P(E₂) = \(\frac{13}{52}=\frac{1}{4}\)
Then, P(E₁ ∩ E₂) = P(E₁) . P(E₂)
= \(\frac{1}{2} \cdot \frac{1}{4}\)
= \(\frac{1}{8}\)
[Since, E₁ and E₂ and independent events]

Question 12.
In a symmetrical distribution the coefficient of skewness will be:
(a) 0
(b) Q₁
(c) Q₃
(d) 1
Answer:
(a) 0
Explanation:
For symmetrical distribution,
Mean = Median = Mode
So, in the case of symmetrical distribution, the coefficient of skewness will be zero.

Question 13.
If I tell you that you scored at the 55th percentile on your final exam, you would know
(a) 55% of the class scored as good or worse than I did
(b) I earned 55% on the exam
(c) I failed the exam
(d) 45% of the class scored worse than I did
Answer:
(a) 55% of the class scored as good or worse than I did
Explanation:
Scoring at the 55th percentile generally means you scored better than 55% of your class. Therefore, 55% of the class scored as good or worse than you did and 45% of the class scored better than you did. So, 55% of class scored as good or worse than I did is true.

Question 14.
The meaning of kWh is
(a) kilo-Watt-hour
(b) kilo Watt
(c) Kelvin-Watt
(d) Kelvin-Watt -hour
Answer:
(a) kilo-Watt-hour
Explanation:
A Watt-hour (Wh) and a kilo Watt-hour (kWh) are units of energy, where 1000 Wh = 1 kWh.

Question 15.
The income tax act was passed in the year
(a) 1947
(b) 1950
(c) 1961
(d) 1991
Answer:
(c) 1961
Explanation:
The income tax act was passed in the year 1961.

Question 16.
The compound interest on ₹ 30,000 at 7% per annum is ₹ 4347. This period (in years) is
(a) 2
(b) 2\(\frac{1}{2}\)
(c) 3
(d) 4
Answer:
(a) 2
Explanation:
Amount = ₹(30,000 + 4347) = ₹ 34347
Let the time be n years.
Then, using formula of compound interest
A_n = P(1 + i)ⁿ
Here, A_n = 34347, i = \(\frac{7}{100}\) = 0.07 and P = 30,000
∴ 34347 = 30,000 (1 + 0.07)ⁿ
⇒ (1.07)ⁿ = \(\frac{34347}{30000}\)
⇒ \(\left(\frac{107}{100}\right)^n=\frac{11449}{10000}\)
⇒ \(\left(\frac{107}{100}\right)^n=\left(\frac{107}{100}\right)^2\)
⇒ n = 2 years

Question 17.
The distance between P(x₁, y₁) and Q(x₂, y₂) when PQ is parallel to Y-axis is
(a) |y₁ – y₂|
(b) |x₁ – x₂|
(c) |y₁ + y₂|
(d) |x₁ + x₂|
Answer:
(a) |y1 – y₂|
Explanation:
If PQ is parallel to Y-axis, then x₁ = x₂
∴ Distance, PQ = \(\left|\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\right|\) = |y₁ – y₂|

Question 18.
The distance of the point (-1, 1) from the line 12(x + 6) = 5(y – 2) is
(a) 2 units
(b) 3 units
(c) 4 units
(d) 5 units
Answer:
(d) 5 units
Explanation:
The given line is 12(x + 6) = 5(y – 2)
⇒ 12x – 5y + 82 = 0
∴ Distance of (-1, 1) from 12x – 5y + 82 = 0 is
d = \(\frac{|12(-1)-5.1+82|}{\sqrt{(12)^2+(-5)^2}}\)
= \(\frac{|-12-5+82|}{\sqrt{169}}\)
= \(\frac{65}{13}\)
= 5 units

Direction (Q.19 & Q.20): In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.

Question 19.
Assertion (A): A can do a certain job in 12 days, B is 60% more efficient than A. Then B alone takes 7.5 days to do the same job.
Reason (R): A can do a certain job in 12 days, B is 60% more efficient than A. Then B alone takes 8 days to do the same job.
Answer:
(c) (A) is true but (R) is false.
Explanation:
Ratio of times taken by A and B is 160 : 100 = 8 : 5
Suppose B alone take x days to do the same job.
Then, 8 : 5 :: 12 : x
⇒ \(\frac{8}{5}=\frac{12}{x}\)
⇒ x = \(\frac{12 \times 5}{8}\)
⇒ x = 7\(\frac{1}{2}\) days
Hence, B can alone do the job in 7.5 days.

Question 20.
Assertion (A): If the central movement μ₁, μ₂, μ₃ and μ₄ are 0, 6, 31 and 108, respectively. Then coefficient of kurtosis 3 and curve mesokurtic.
Reason (R): coefficient of kurtosis, β₂ = \(\frac{\mu_4}{\mu_2^2}\)
Answer:
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
Explanation:
Since, coefficient of kurtosis,
\(\beta_2=\frac{\mu_4}{\mu_2^2}=\frac{108}{(6)^2}\) = 3
Also, here β₂ = 3, then curve is mesokurtic.

Section-B

(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 21.
Arrange the following words in a logical and meaningful order.
1. Country
2. Furniture
3. Forest
4. Wood
5. Trees
Answer:
From the given words, we can say that country contains forest, forest has trees, trees have wood that is used to make furniture, Hence, the correct order of the given words is 1, 3, 5, 4, 2.

Question 22.
A die is rolled. If E = (1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5}, find P[(E ∩ F)/G].
OR
A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that all the three balls are white.
Answer:
Given, E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5}
P(E) = \(\frac{3}{6}=\frac{1}{2}\), P(F) = \(\frac{2}{6}=\frac{1}{3}\) and P(G) = \(\frac{4}{6}=\frac{2}{3}\)
Also, P(E ∩ F) = \(\frac{1}{6}\)
and P(E ∪ F) = P(E) + P(F) – P(E ∩ F) = \(\frac{2}{3}\)
(E ∩ F) ∩ G = {3}
P[(E ∩ F) ∩ G] = \(\frac{1}{6}\)
Therefore, \(P \frac{[(E \cap F)]}{G}=P \frac{[(E \cap F) \cap G]}{P(G)}\)
= \(\frac{\frac{1}{6}}{\frac{2}{2}}\)
= \(\frac{1}{4}\)
OR
Given, Number of red balls = 8
and number of white balls = 5
(i) P(all the three balls are white) = \(\frac{{ }^5 C_3}{{ }^{13} C_3}\)
= \(\left(\frac{\frac{5 \times 4}{2}}{\frac{13 \times 12 \times 11}{3 \times 2}}\right)\)
= \(\frac{5 \times 4 \times 3}{13 \times 12 \times 11}\)
= \(\frac{5}{143}\)

Question 23.
If Q₁ = 26, Q₂ = 46 and Q₃ = 76, find coefficient of skewness.
OR
While computing rank correlation coefficient between profits and investment for 10 years of a firm, the difference in rank for a year was taken as 7 instead of 5 by mistake and the value of rank correlation coefficient was computed as 0.80. What would be the correct value of rank correlation coefficient after rectifying the mistake?
Answer:
Here, we use the method of Bowley’s coefficient of skewness

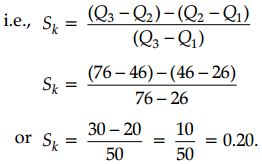
OR
We are given that n = 10
r_s = 0.80 and the wrong d = 7 should be replaced by 5.

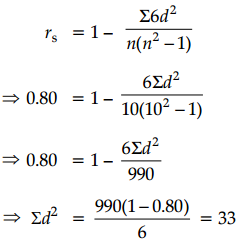
Corrected Σd² = 33 – 72 + 52 = 9
Hence, rectified value of rank correlation coefficient = 1 – \(\frac{6 \times 9}{10 \times\left(10^2-1\right)}\) = 0.95

Question 24.
What is the monthly interest rate equivalent to an annual rate of 8% capitalized quarterly? [Given (1.04)^1/6 = 1.006558]
Answer:
Here, rate of 8%, capitalized quarterly
i.e., i = \(\frac{8}{2}\)% = 4% bi-annually
So, ibian = 4%
We know,

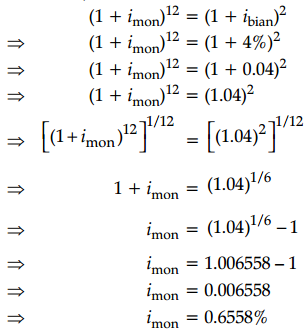
Questions 25.
A man purchased a house valued at ₹ 300000. He paid ₹ 200000 at the time of purchased and agreed to pay the balance with the interest at 12% per annum compounded half yearly in 20 equal half yearly installments. If first installment is paid after six months from the date of purchase then find the amount of each installment. [Given that (1.06)²⁰ = 3.2071]
Answer:
Here, Present value = 300000 – 200000 = ₹ 100000
i = 12% half yearly
= \(\frac{12}{100} \times \frac{1}{2}\)
= 0.06
n = 20

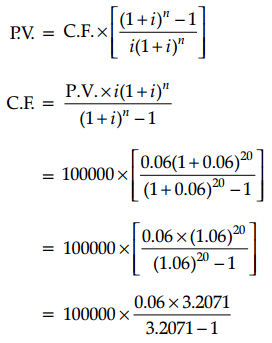
= 100000 × \(\frac{0.1924}{2.2071}\)
= 100000 × 0.0871845
= 8718.45
= ₹ 8719 (approx)
Hence, ₹ 8719 is the amount of each installment.

Section-C

(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 26.
Find the number of squares that can be formed on 8 × 8 chessboard?
OR
Using the digits 0, 1, 2, 2, 3, how many numbers greater than 20000 can be made?
Answer:
The number of squares in a n × n chess board will be Σn²; n varying from 1 to n.
Now, Σn² = 1² + 2² + 3² + ….. + n²
Σn² = \(\frac{n(n+1)(2 n+1)}{6}\) ……(i)
Put n = 8 in equation (i), we get
Σ8² = \(\frac{8 \times(8+1)(2 \times 8+1)}{6}\)
= \(\frac{8 \times 9 \times 17}{6}\)
= 204
OR
Total number of digits = 0, 1, 2, 2, 3
Total number formed by these digits = \(\frac{5 !}{2 !}=\frac{120}{2}\) = 60
Total number formed by starting 0 = \(\frac{4 !}{2 !}=\frac{24}{2}\) = 12
Total number formed by starting 1 = \(\frac{4 !}{2 !}=\frac{24}{2}\) = 12
Total number formed greater than 20000 = 60 – 12 – 12 = 36

Question 27.
Read the following information carefully to answer the questions given below.
(I) ‘A + B’ means ‘A is the father of B’
(II) ‘A – B’ means ‘A is the wife of B’
(III) ‘A × B’ means ‘A is the brother of B’
(IV) ‘A ÷ B’ means ‘A is the daughter of B’

(i) If P × R ÷ Q, which of the following is true?
(a) P is uncle of Q
(b) P is the father of Q
(c) P is the brother of Q
(d) P is the son of Q
(e) None of these

(ii) If P × R – Q, which of the following is true?
(a) P is brother-in-law of Q
(b) P is the brother of Q
(c) P is the uncle of Q
(d) None of these
Answer:
(i) Clearly, from the information given in the question, R is the daughter of Q and P is the brother of R.
Therefore, P is son of Q.
Hence, statement (d) is true.

(ii) Clearly, from the information R is the wife of Q, and P is the brother of R.
Therefore, P is related as brother-in-law to Q.
Hence, statement (a) is true.

Question 28.
\(\lim _{x \rightarrow 0}\left(\frac{\sqrt{1+x^2}-\sqrt{1+x}}{\sqrt{1+x^3}-\sqrt{1+x}}\right)=?\)
Answer:

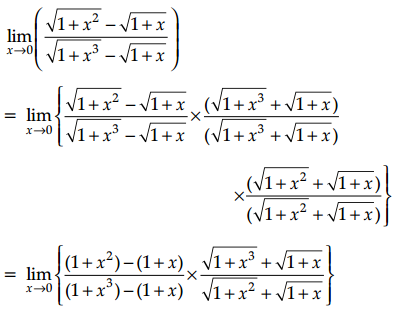
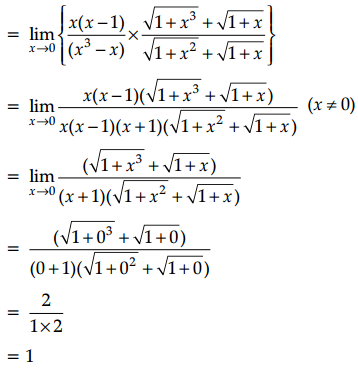
Question 29.
Following is the distribution of marks obtained by 50 students in a class test:

Marks more than	0	10	20	30	40	50
No. of Students	50	42	38	28	16	3

If 60% of the students pass the test, find the minimum marks obtained by a pass student.
Answer:
First we prepare the following cumulative frequency table:

Marks	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50	≥ 50
No. of Students (f)	8	4	10	12	13	3
Cumulative Frequency	8	12	22	34	47	50

Here, n = 50
As 60% students pass the test, it means that 40% students get less than minimum passing marks.
Hence, the minimum passing marks are P40.

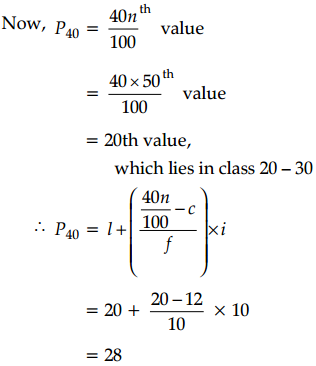
Hence, minimum passing marks are 28.

Question 30.
A dealer is in Jhansi buys some articles worth ₹ 8,000. If the rate of GST is 18%, find how much will the dealer pay for the articles bought.
Answer:
In a case of Intra-state transaction,
Cost of an article = ₹ 8,000 and GST rate = 18%
∴ CGST = 9% of ₹ 8,000
= ₹ \(\frac{9}{100}\) × 8,000
= ₹ 720
SGST = 9% of ₹ 8,000
= ₹ \(\frac{9}{100}\) × 8,000
= ₹ 720
and IGST = ₹ 0
The dealer paid = ₹ (8000 + 720 + 720 + 0) = ₹ 9440

Question 31.
Find the equation of the circle which passes through the point (-2, -3) and has its centre on the negative direction of X-axis and is of radius 5 units.
OR
Find the co-ordinates of points on parabola y² = 8x, whose focal distance is 4.
Answer:
As the centre of the circle lies on the negative direction of X-axis, let its centre be C(h, 0), h < 0.
Since, the circle passes through A(-2, -3) and has radius 5.
∴ CA = 5
⇒ (h + 2)² + (0 + 3)² = 5²
⇒ (h + 2)² = 25 – 9 = 16
⇒ h + 2 = ±4
⇒ h = 2 or h = -6
But h < 0, therefore h = -6
∴ The centre of the circle is (-6, 0) and its equation is {x – (-6)}² + (y – 0)² = 5²
⇒ (x + 6)² + y² = 25
⇒ x² + y² + 12x + 11 = 0
OR
Given equation of the parabola is y² = 8x
i.e., y² = 4 × 2 × x
∴ a = 2, focus, S = (2, 0)
Let P(x, y) be any point on the parabola, then PS = 4
i.e., \(\sqrt{(x-2)^2+(y-0)^2}\) = 4
⇒ x² – 4x + 4 + 8x = 16
⇒ x² + 4x – 12 = 0
⇒ (x + 6)(x – 2) = 0
⇒ x = -6 or x = 2
when x = -2, y² = 16
⇒ y = ±4
when x = -6, y² = -48
⇒ y = \(\sqrt{-48},\), not possible
Hence, the coordinates of point P are (2, 4) and (2, -4).

Section-D

(This section comprises long answer type questions (LA) of 5 marks each)

Question 32.
(i) Find the value of \(\left(\frac{x^a}{x^b}\right)^{a+b} \times\left(\frac{x^b}{x^c}\right)^{b+c} \times\left(\frac{x^c}{x^a}\right)^{c+a}\)
(ii) Find the value of \(\left[\left\{(2)^{1 / 2} \cdot(4)^{3 / 4} \cdot(8)^{5 / 6} \cdot(16)^{7 / 8} \cdot(32)^{9 / 10}\right\}^4\right]^{4 / 25}\)
OR
Using the world population formula P = 6.9(1.011)^t, where t is the number of years after 2011 and P is the word population in billion and 6.9 billion people in 2011 is the world population in billions of people, estimate
(a) the population in the year 2050 to the nearest hundred million, and
(b) by what year will the population be double what it was in 2011.
Answer:


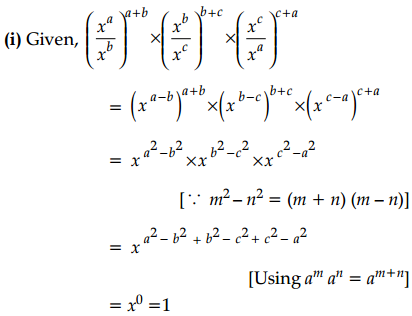
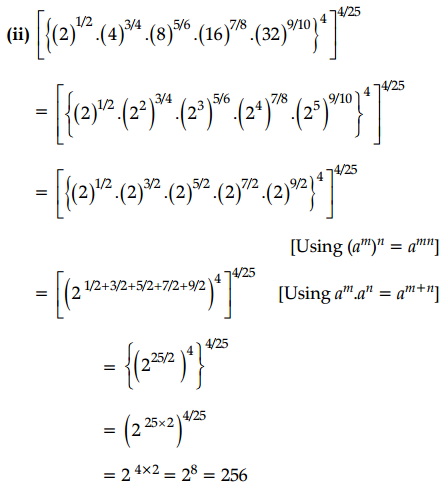
OR
(a) Here, t = 2050 – 2011 = 39
∴ P = 6.9 (1.011)³
Taking log on both sides, we get
log₁₀ P = log₁₀ [6.9(1.011)³⁹]
⇒ log₁₀ P = log₁₀ (6.9) + log₁₀ (1.011)³⁹
[Applying rule log_a (mn) = log_a m + log_a n]
⇒ log₁₀ P = log₁₀ (6.9) + 39 log₁₀ (1.011)
[Applying rule log_a mⁿ = n log_a m]
⇒ log₁₀ P = 0.83884 + 39(0.00475)
⇒ log₁₀ P = 0.83884 + 0.18525 [By using log table]
⇒ log₁₀ P = 1.02409
⇒ log₁₀ P = antilog10 (1.02409)
⇒ P = 10.57 ≅ 10.6 [By using antilog table]
Hence, the population in 2050 will be about 10.6 billion people.
(b) Here, P = 2(6.9) = 13.8
Now, 13.8 = 6.9(1.011)^t
⇒ 2 = (1.011)^t
Taking log on both sides, we get
log 2 = log (1.011)^t
⇒ log 2 = t log (1.011)
[Applying rule log_a mⁿ = n log_a m]
⇒ t = \(\frac{\log 2}{\log (1.011)}\)
⇒ t = \(\frac{0.3010}{0.00475}\)
⇒ t = 63.359 ≅ 64
Thus, the population will be double (i.e., 13.8 billion people) the 2011 population by the year = 2011 + 64 = 2075.

Question 33.
The sum of an infinite G.P. is 57 and the sum of the cubes of its term is 9747, find the G.P.
OR
Find the number of all possible arrangements of the letters of the word “MATHEMATICS” taken four form at a time.
Answer:
Let the first term of G.P be ‘a’ and the common ratio be ‘r’ where -1 < r < 1
The G.P is a, ar, ar² …..
Therefore the sum of the infinite terms of the G.P is
\(\frac{a}{1-r}\) = 57 …….(i)
If taking the cube of each term, the new G.P is a³, a³r³, a³r⁶, ……..
Therefore the sum of the infinite terms of their cube is
\(\frac{a^3}{1-r^3}\) = 9747 …….(ii)
Taking the cube of the (i)
\(\frac{a^3}{(1-r)^3}\) = (57)3
⇒ a³ = (57)³(1 – r)³ ……(iii)
Substituting the value of ‘a’ in terms of r in equation (ii), we get
\(\frac{(57)^3(1-r)^3}{1-r^3}\) = 9747
⇒ \(\frac{(1-r)^3}{(1-r)\left(1+r^2+r\right)}=\frac{9747}{(57)^3}\)
⇒ \(\frac{(1-r)^2}{\left(1+r^2+r\right)}=\frac{1}{19}\)
⇒ \(\frac{1+r^2-2 r}{1+r^2+r}=\frac{1}{19}\)
⇒ 19(1 + r² – 2r) = 1 + r² + r
⇒ 18r² – 39r + 18 = 0
⇒ 6r² – 13r + 6 = 0
⇒ 6r² – 9r – 4r + 6 = 0
⇒ (2r – 3)(3r – 2) = 0
Therefore, r = \(\frac{3}{2}\) or r = \(\frac{2}{3}\) since r < 1.
∴ r = \(\frac{2}{3}\)
Substitute in equation (i),
\(\frac{a}{1-\frac{2}{3}}\) = 57
⇒ 3a = 57
⇒ a = 19
Thus, the first term of the G.P is 19 and the common ratio is \(\frac{2}{3}\).
The G.P is 19, \(\frac{38}{3}\), \(\frac{76}{9}\) and so on.
OR
The word MATHEMATICS consists of 11 letters
(M, M), (A, A), (T, T), H, E, I, C, S
Case 1: In this case 2 similar and 2 similar letters are selected,
number of arrangements = \({ }^3 C_2 \times \frac{4 !}{2 ! 2 !}\) = 18.
Case 2: In this case, 2 similar and 2 different letters are selected,
number of arrangements = \({ }^3 C_1 \times{ }^7 C_2 \times \frac{4 !}{2 !}\) = 756.
Case 3: In this case all 4 letters selected are different, number of arrangements = ⁸C₄ × 4! = 1680.
Therefore, total number of arrangements = 18 + 756 + 1680 = 2454.

Question 34.
(i) Find the derivative of f(etan x) w.r.t. x at x = 0. It is given that f'(1) = 5.
(ii) If \(x \sqrt{1+y}+y \sqrt{1+x}=0\) and x ≠ y prove that \(\frac{d y}{d x}=-\frac{1}{(x+1)^2}\).
Answer:
(i) Given f(etan x)
∴ y = f(etan x)
\(\frac{d y}{d x}=f^{\prime}\left(e^{\tan x}\right) \frac{d}{d x}\left(e^{\tan x}\right)\)

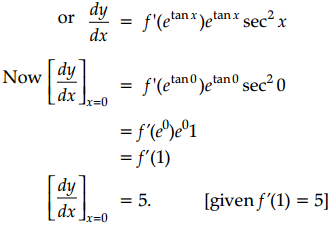
(ii) Given, equation is \(x \sqrt{1+y}+y \sqrt{1+x}=0\)
⇒ \(x \sqrt{1+y}=-y \sqrt{1+x}\)
On squaring both sides, we get
⇒ x² (1 + y) = y² (1 + x)
⇒ x² + x²y = y² + y²x
⇒ x² – y² = y²x – x²y
⇒ (x + y)(x – y) = -xy(x – y)
⇒ (x – y)(x + y) + xy(x – y) = 0
⇒ (x – y)(x + y + xy) = 0
∴ Either x – y = 0 or x + y + xy = 0
Now, x – y = 0 or x = y
But it is given that x ≠ y. So, it is a contradiction.
∴ x – y = 0 is rejected.
Now, consider y + xy + x = 0
⇒ y(1 + x) = -x
⇒ y = \(\frac{-x}{1+x}\) …….(i)
On differentiating both sides w.r.t. x, we get

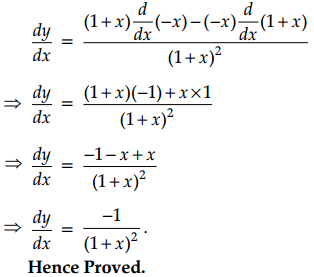
Question 35.
For an industrial connection monthly consumption of electricity units are 550, calculate the electricity bill. Tariff rates can be considered the table given below.

Unit Slab	Rate Per Unit (in ₹)	Fixed Charge
1-300	7.50	330
301-500	8.40	390
501 and above	8.75	450

Answer:

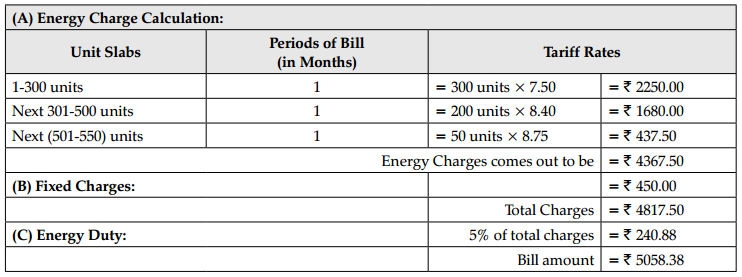
Thus, the final bill amount is ₹ 5058.38.

Section-E

(This section comprises 3 source-based questions (Case Studies) of 4 marks each)

Question 36.
In junior school children were performing science experiments in the laboratory. The experiments were conducted under the supervision of teacher. Each student would obtain the marks for successful experiment. The marks obtained by 5 students in the experiment test for 25 marks are 8, 13, 12, 15, 22.

On the basis of this information answer the following questions:
(i) Find the mean of the given data.
(ii) Define range.
(iii) What is the variance of the given data?
OR
What is the Standard Deviation of the data?
Answer:
(i) Mean = \(\frac{12+8+13+15+22}{5}\) = 14
(ii) Difference between maximum value of data and minimum value of data is called range.
(iii) Since, mean (\(\bar{x}\)) = 14

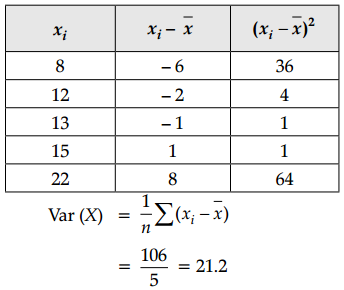
OR
From above Variance (Var.) = 21.2
S.D. = \(\sqrt{Variance}\)
= \(\sqrt{21.2}\)
= 4.604

Question 37.
A man took a loan from the bank of ₹ 32500. He started paying ₹ 200 in the first month and then increase the payment by ₹ 150 every month.

On the basis of this information answer the following questions:
(i) What type of series is formed, when he increases his amount by ₹ 150 every month?
(ii) What will be the nth term of this series?
OR
How much amount he pay in the sixth month?
(iii) After how many months (approx) the loan will be cleared?
Answer:
(i) 200, 350, 500,……
It forms an A.P

(ii) Using formula, T_n = a + (n – 1)d
we get a_n = 200 + (n – 1) × 150
= 200 – 150 + 150n
= 50 + 150n
OR
We know that, T_n = a + (n – 1)d
Here, a = 200, d = 150
∴ T₆ = 200 + 5 × 150
= 200 + 750
= 950

(iii) S_n = \(\frac{n}{2}\)[2 × 200 + (n – 1) × 150]
⇒ 32500 = \(\frac{n}{2}\)[250 + 150n]
⇒ 75n² + 125n = 32500
⇒ 3n² + 5n – 1300 = 0
⇒ (n – 20)(3n + 65) = 0
⇒ n = 20 [∵ n ≠ \(\frac{-65}{3}\)]

Question 38.
A child’s game has 8 triangles of which 3 are blue and rest are red, and 10 squares of which 6 are blue and rest are red. One piece is lost at random.

(i) How many triangles are of red colour and how many squares are of red colour? Find the probability that lost piece is triangle.
OR
(ii) Find the probability that lost piece is square. Also, find the probability that lost piece is triangle of red colour.
Answer:
(i) Since, total no. of triangles = 8
Triangles with blue colour = 3
Triangles with red colour = 8 – 3 = 5
and total no. of squares = 10
Squares with blue colour = 6
Squares with red colour = 10 – 6 = 4
Number of favourable outcomes for the event that lost figure is triangle,
i.e., F(E) = 8
Total figures (square and triangle) = 8 + 10 = 18
i.e., T(E) = 18
Probability (getting a triangle),
P(E) = \(\frac{F(E)}{T(E)}\)
T(E) = \(\frac{8}{18}=\frac{4}{9}\)
OR
(ii) Number of favourable outcomes for the events that squares is lost,
i.e., F(E) = 10
T(E) = 8 + 10 = 18
P(getting a square), P(E) = \(\frac{10}{18}=\frac{5}{9}\)
Number of favourable outcomes for the event that lost figure is triangle of red colour = 5,
i.e., F(E) = 5 and T(E) = 18
P(lost figure is red triangle), P(E) = \(\frac{5}{18}\)