Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 6 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 6 with Solutions
Time : 2 Hr.
Max. Marks : 40
General Instructions:
- The question paper consists of 14 questions divided into three Sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.
Section – A
Question 1.
Solve : \(\sqrt{3} x^{2}-2 \sqrt{2} x-2 \sqrt{3}\) = 0. (2)
Solution:

Question 2.
From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. What will be it the radius of the circle (in cm)? (2)
Solution:
Given,
PQ = 13 cm and OQ = 12 cm
In ∆OPQ, by pythagoras theorem
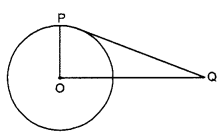
Thus, r = PO \(\sqrt{\mathrm{PQ}^{2}-\mathrm{OQ}^{2}}\)
= \(\sqrt{(13)^{2}-(12)^{2}}\)
= \(\sqrt{169-144}=\sqrt{25}\)
As length cannot be negative.
Question 3.
If the nth term of an A.P. is (2n + 1), then find the sum of its first three terms. (2)
Solution:
Here, an = 2n + 1
a1 = 2(1) + 1 = 3
a2 = 2(2) + 1 = 5
a3 = 2(3) + 1 = 7
∴ a1 + a2 + a3 = 3 + 5 + 7 = 15.
Question 4.
The median of the following frequency distribution will be : (2)
| X | 6 | 7 | 5 | 2 | 10 | 9 | 3 |
| y | 9 | 12 | 8 | 13 | 11 | 14 | 7 |
Solution:
| x | f | c.f. | x | f | c.f |
| 2 | 13 | 13 | 7 | 12 | 49 |
| 3 | 7 | 20 | 9 | 14 | 63 |
| 5 | 8 | 28 | 10 | 11 | 74 |
| 6 | 9 | 37 |
Here, \(\frac { N }{ 2 }\) = \(\frac { 74 }{ 2 }\) = 37th observation
Median = 37th observation = 6.
∴ Radius of hemisphere = Radius of cone
Question 5.
A solid is hemispherical at the bottom and conical (of same radius) above it. If the surface area of the two are equal then find the ratio of the radius and the slant height of the conical part. (2)
Solution:
Given,
Also, Curved surface area of hemisphere = Curved surface area of cone
⇒ 2πr² = πrl [where l = slant height of the cone]
⇒ 2r = 1
⇒ r : 1 = 1 : 2.
Question 6.
The roots of the quadratic equation x² – 0.04 = 0. (2)
OR
The difference in the roots of the equation 2x² – 11x + 5 = 0.
Solution:
Given : x² – 0.04 = 0
⇒ x² – (0.2)² = 0
⇒ (x + 0.2) (x – 0.2) = 0
⇒ x = – 0.2, 0.2
OR
Let α and ß be the root of this quadratic equation
2x² – 11x + 5 = 0
α + ß =(11/2)
α.ß = (5/2)
We know that,
(α – ß)² = (α + ß)² – 4 α.ß
= \(\left(\frac{11}{2}\right)^{2}-4\left(\frac{5}{2}\right)\)
= \(\frac{121}{4}-\frac{20}{2}=\frac{121-40}{4}=\frac{81}{4}=\left(\frac{9}{2}\right)^{2}\)
Difference of roots = (α – ß) = 4.5
Section – B
Question 7.
Consider the frequency distribution of the heights of 60 students of a class : (3)
| Height (in cm.) | No. of students | Cumulative frequency |
| 150 – 155 | 16 | 16 |
| 155 – 160 | 12 | 28 |
| 160 – 165 | 9 | 37 |
| 165 – 170 | 7 | 44 |
| 170 – 175 | 10 | 54 |
| 175 – 180 | 6 | 60 |
Find the sum of the lower limit of the modal class and the upper limit of the median class.
Solution:
Class having maximum frequency is the modal class.
Hence, modal class 150 -155.
Lower limit of the modal class = 150
Now, \(\frac {1}{2}\) = \(\frac {60}{2}\) =30
The cumulative frequency just greater than 30 is 37.
Hence, the median class is 1360 – 165.
Upper limit of the median class = 165
Required sum = 150 + 165 = 315
Question 8.
The angle of elevation of the top of a tower at a point on the ground is 30°. If the height of the tower is tripled, find the angle of elevation of the top of the same point.
OR
The tops of two towers of height x and ij, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x : y. (3)
Solution:
Let the height of the tower AB be h m and the distance between the tower and the point of observation C on the ground be y m.
So, tan 30° = \(\frac {h}{y}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{y}\)
⇒ y = h\(\sqrt{3}\)
Let the new height be DB and the new angle of elevation be x°.
So
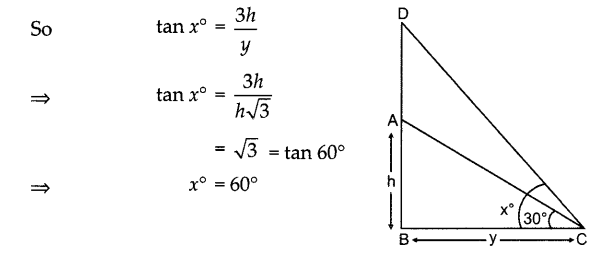
Thus, the angle of elevation is 60° from the same point when the height of the tower is tripled.
OR
Let AB and CD be two towers of height x and y respectively.
M is the mid-point of BC i.e., BM = MC
In ∆ABM, we have
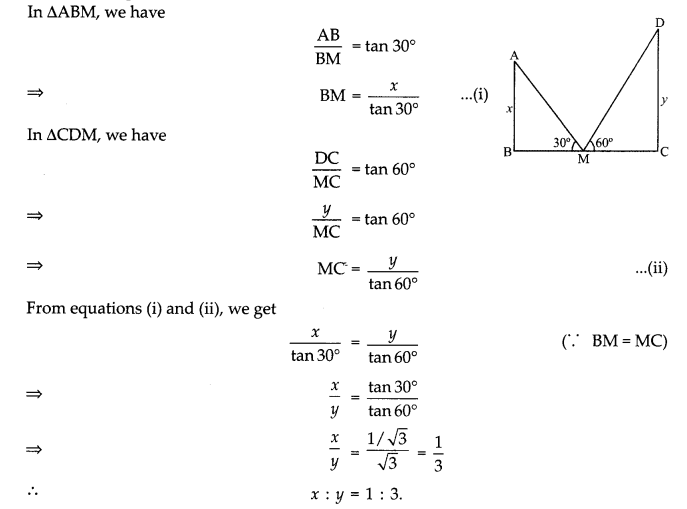
Question 9.
Draw a line-segment AB of length 8 cm. Taking A as centre draw a circle of radius 4 cm and taking B as centre, draw another circle B of radius 3 cm. Construct tangents to each circle from the centre of the other circle. (3)
Solution:
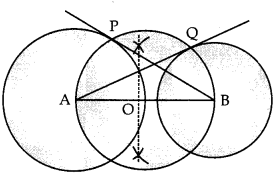
Step I: Draw AB = 8 cm.
Step II: Construct a circle of radius 4 cm from point A.
Step III: Construct another circle of radius 3 cm from point B.
Step IV : Now draw perpendicular bisector of AB. Let O be the mid-point of AB.
Step V : Keeping O as the centre, draw circle with AO – OB as the radius.
Step VI: Mark point of intersection of this circle with the larger circle as P.
Step VII: Draw PB as tangent to the larger circle.
Step VIII: Similarly, mark the point of intersection of the circle with centre O with the smaller circle as Q.
Step IX : Draw AQ as the tangent to the smaller circle.
Question 10.
Following table gives the ages in years of militants operating in a certain area of a country. (3)
| Age (in years) | 40-43 | 43-46 | 46-49 | 49-52 | 52-54 |
| Number of militants | 31 | 58 | 60 | k | 27 |
If mean of the above distribution is 47.2, find how many militants in the age groups 49-52 are active in the area?
Solution:
| Class Interval | Frequency (fi) | xi | fixi |
| 40-43 | 31 | 41.5 | 1286.5 |
| 43-46 | 58 | 44.5 | 2581 |
| 46-90 | 60 | 47.5 | 2850 |
| 49-52 | k | 50.5 | 50.5k |
| 52-55 | 27 | 53.5 | 1444.5 |
| ∑fi = 176 + k | ∑fi = 8162 + 50.5 k |
Mean (\(\bar { x }\) ) = 47.2
We know that,
\(\bar{x}=\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}\)
⇒ \(47.2=\frac{8162+50.5 k}{176+k}\)
⇒ 47.2(176 + k) = 8162 + 50.5k
⇒ 8307.2 + 47.2k = 8162 + 50.5k
⇒ 8307.2 – 8162 = 50.5k – 47.2k
⇒ 145.2 = 3.3 k
⇒ k = \(\frac{145.2}{3.3}\) = 44
Thus, there are 44 militants operating in the age group 49 – 52.
Section – C
Question 11.
If Sn denotes the sum of the first n terms of an A.P., prove that S30 = 3(S20 – S10). (4)
OR
Find the sum of the following :
\(\left(1-\frac{1}{n}\right)+\left(1-\frac{2}{n}\right)+\left(1-\frac{3}{n}\right)\) …. upto n terms.
Solution:
Let a be the first term of the series and d be the common difference.
∴ Sn = \(\frac {n}{2}\){2a + (n – 1)d}
So, 30
S30 = \(\frac {30}{2}\) {2a + (30 – 1)d}
⇒ S30 = 15{2a + 29d]
S20 = \(\frac {20}{2}\) {2a + (20 – 1 )d] … (i)
S20 = 10{2A + 19d) … (ii)
and S20 = \(\frac {10}{2}\){2a + (10 – 1)d}
⇒ S10 = 5{2a + 9 d] … (iii)
Now, S20 – S10 = 10{2a + 19d} – 5{2a + 9d}
= 20a + 190d – 10a – 45d
= 10a+145d
= 5(2a + 29d )
3(S20 – S10) = 3[5 (2a + 29d] [From (iii)]
S30 = 15 (2a + 29d) [From (i)]
Thus, 3(S20 – S10) = S30
OR
Given,
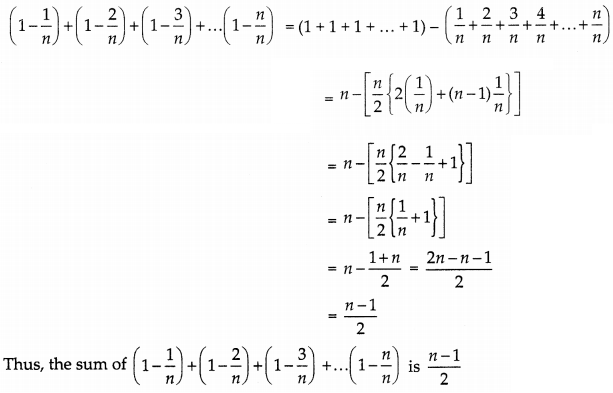
Question 12.
In Fig. PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. Find the length of TP. (4)
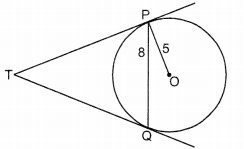
Solution:
Join OT, let it intersect PQ at the point R.
Now, ∆TPQ is an isosceles triangle and TO is the angle bisector of ∠PTQ. So, OT ⊥ PQ and therefore, OT bisects PQ
∴ PR = RQ = 4 cm
Also, OR = \(\sqrt{\mathrm{OP}^{2}-\mathrm{PR}^{2}}=\sqrt{5^{2}-4^{2}}\)
= \(\sqrt{25-16}\)
= \(\sqrt{9}\)
= 3 cm
Now, ∠TPR + ∠RPO = 90° = ∠TPR + ∠PTR [∵In ∆TRP, ∠TRP = 90° ]
⇒ ∠RPO = ∠PTR
So, ∆TRP ~ ∆PRO (By AA rule)
∴ \(\frac{\mathrm{TP}}{\mathrm{PO}}=\frac{\mathrm{RP}}{\mathrm{RO}}\)
or \(\frac{\mathrm{TP}}{5}=\frac{4}{3}, \text { or } \mathrm{TP}=\frac{20}{3} \mathrm{~cm}\)
Hence, the length of TP = \(\frac{20}{3}\) cm.
Question 13.
A circus artist is showing stunts in a show climbing through a 15 m long rope which is highly stretched and tied from the top of a vertical pole to the ground as shown below: (4)
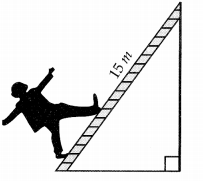
Answer the following questions.
(i) What is the height of the pole, if angle made by rope to the ground level is 45°?
(ii) If the angle made by the rope to the ground level remains same, then find the distance between artist and pole at ground level.
Solution:

Question 14.
Mathematics teacher of a school took her 10th standard students to show Gol Gumbaz. It was a part of their Educational trip. The teacher had interest in history as well. She narrated the facts of Gol Gumbaz to students. Gol Gumbaz is the tomb of King Muhammad Adil Shah, Adil Shah Dynastry. Construction of the tomb, located in Vijayapura, Karanataka, India, was started in 1626 and completed in 1656. Then the teacher said in this monument one can find combination of solid figures. She pointed that there are cubical bases and hemispherical dome is at the top. (4)

(i) Find the diagonal of the cubic portion of the Gol Gumbaz, if one side of cubical portion is 23 m.
(ii) A block of Gol Gumbaz is in the shape of a cylinder of diameter 0-5 cm with two hemispheres stuck to each of its ends. The length of shape is 2 cm. What is the volume of the block. (Use π = 3.14)
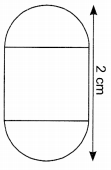
Solution:
(i) Diagonal of cubic portion = a\(\sqrt{3}\)
= 23\(\sqrt{3}\) m
(ii) Volume of the block = πr²h + 2 x \(\frac{2}{3}\) x πr³
\(\pi r^{2}\left[h+\frac{4}{3} r\right]\)
= \(3.14 \times(0.25)^{2}\left[1.5+\frac{4}{3} \times 0.25\right]\) [∵h = 2 – 2 x 0.25 = 1.5]
= \(3.14 \times(0.25)^{2} \times \frac{5.5}{3}\)
= 0.36 cm³ (approx.)