CBSE Sample Papers for Class 10 Maths Standard Set 3 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths Standard with Solutions and marking scheme Set 3 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Standard Set 3 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 MCQs carrying 1 mark each
3. Section B has 5 questions carrying 02 marks each.
4. Section C has 6 questions carrying 03 marks each.
5. Section D has 4 questions carrying 05 marks each.
6. Section E has 3 case based integrated units of assessment (04 marks each) with sub parts of the values of 1, 1 and 2 marks each respectively.
7. All Questions are compulsory. However, an internal choice in 2. Qs of 5 marks, 2.Qs of 3 marks and 2. Questions of 2. marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take n = 22/7 wherever required if not stated.

Section – A ( 20 Marks) 
Section A Consists of Multiple Choice Type questions of 1 mark each

Question 1.
√n is a natural number such that n > 1
Which of these can DEFINITELY be expressed as a product of primes?
(i) √n
(ii) n
(iii) \(\frac{\pi}{2}\)
(A) Only (ii)
(B) Only (i) and (ii)
(C) All (i), (ii) and (iii)
(D) Cannot be determined with knowing n
Solution:
(B) Only (i) and (ii)

Explanation: Natural Prime number (n) which are perfect squares are product of prime numbers.

Question 2.
In the given figure, AD is the bisector of ∠A. If BD = 4 cm, DC = 3 cm, and AB = 6 cm, then the value of AC is [1]

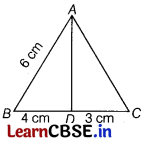
(a) 4 cm
(b) 4.5 cm
(c) 6 cm
(d) 5 cm
Answer:
(b) 4.5 cm

In ∆ABC, AD is the bisector of ∠A.
∴ \(\frac{B D}{D C}\) = \(\frac{A B}{A C}\) [by angle bisector theorem]
⇒ \(\frac{4}{3}\) = \(\frac{6}{A C}\) ⇒ 4 AC = 18
∴ AC = \(\frac{9}{2}\) = 4.5 cm

Question 3.
If a pair of linear equations given by a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 has a unique solution, then which of the following is true?
(A) a₁a₂ = b₁b₂
(B) a₁b₂ ≠ a₂b₁
(C) \(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)
(D) \(\frac{a_1}{b_2} \neq \frac{b_1}{a_2}\)
Solution:
(B) a₁b₂ ≠ a₂b₁

Explanation: For unique solution
\(\frac{a_1}{a_2}≠\frac{b_1}{b_2}\)
a₁b₂ ≠ a₂b₁

Question 4.
If the pair of linear equations 3x + y = 3 and 6x + ky = 8 does not have a solution, then the value of k is [1]
(a) 2
(b) -3
(c) 0
(d) 1
Answer:
(a) 2

Given, 3x + y = 3 and 6x + ky = 8
On comparing the above equation with standard equation ax + by + c = 0, we get
a₁ = 3, b₁ = 1 and c₁ = – 3
and a₂ = 6 b₂ =k and c₂ = -8
Since given equations have no solution,
\(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\) ⇒ \(\frac{3}{6}=\frac{1}{k}\) ⇒ k = 2

Question 5.
4 groups in a class were asked to come up with an arithmetic progression (AP). Shown below are their responses:

Group	Arithmetic progression
M	4, 2, 0,-2, …
N	41, 38.5, 36, 33.5, …
O	-19,-21,-23,-25, …
P	-3, -3, -3,-3, ….

Which of these groups correctly came up with an AP?
(A) only groups M and O
(B) only groups N and O
(C) only groups M, N and O
(D) all groups – M, N, O and P
Solution:
(D) all groups – M, N, O and P

Explanation: Far Group M; a = 4
d = (2 – 4) = (0 – 2)
= (-2 – 0)
= -2 (constant)
For Group N; a =41
d = (385 – 41) = (36 – 38.5)
= (335 – 36)
= -25 (constant)
For Group O; a = -19
d = [-21 – (-19))
= [-23 – (-21)]
= [-25 – (-23)]
= -2 (constant)
For Group P; a = -3
d = [-3 – (-3)l
= [-3 – (-3)]
= [-3 – (-3)]
= 0 (constant)
Thus each term differs from the preceding term by constant value
∴ M, N, O and P all group form A.P.

Question 6.
In ∆PQR, if PS is the internal bisector of ∠P meeting QR at S and PQ =13 cm, QS = (3 + x) cm, SR = (x – 3) cm and PR = 7 cm, then the value of x is [1]
(a) 9 cm
(b) 10 cm
(c) 13 cm
(d) 12 cm
Answer:
(b) 10 cm

Since PS is the internal bisector of ∠P and it meets QR at S.

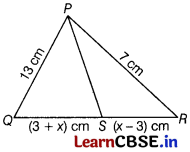
\(\frac{P Q}{P R}=\frac{Q S}{R S}\) [by angle bisector theorem]
⇒ \(\frac{13}{7}=\frac{3+x}{x-3}\)
⇒ 13(x – 3) = 7(3 + x)
⇒ 13x – 39 = 21 + 7x
⇒ 6x = 60
⇒ x = 10 cm

Question 7.
If three points (0, 0), (3, √3) and (3, λ) form an equilateral triangle, then X equals:
(A) 2
(B) -3
(C) -4
(D) None of these
Solution:
(D) None of these

Explanation: Let the given points are A(0, 0), B(3, √3) and C(3, λ).
Since AABC is an equilateral triangle, therefore AB = AC.
⇒ \(\sqrt{(3-0)^2+(\sqrt{3}+0)^2}\) = \(\sqrt{(3-0)^2+(\lambda-0)^2}\)
⇒ 9 + 3 = 9 + λ²
⇒ λ² = 3
⇒ λ = ± √3

Question 8.
cos⁴ x – sin² x is equal to [1]
(a) 2 sin²x – 1
(b) 1 – 2 cos²x
(c) sin²x – cos²x
(d) 2 cos²x – 1
Answer:
(d) 2 cos²x – 1

Given, cos⁴x – sin⁴x
⇒ (cos²x + sin²x) (cos²x – sin²x)
[∵ a² – b² = (a + b) (a – b)]
⇒ 1 . (cos²x – (1 – cos²x))
[∵ sin² A + cos² A = 1 and sin²A = 1 – cos²A]
⇒ cos²x – 1 + cos²x = 2 cos²x – 1

Question 9.
In the figure below, Δ PXY is formed using three tangents to a circle centred at O.

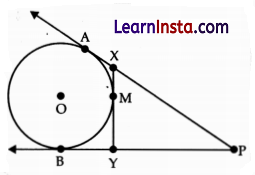
(Note: The figure is not to scale.)
Based on the construction, the sum of the tangents PA and PB is ____________ the perimeter of ΔPXY.
(A) lesser than
(B) greater than
(C) equal to
(D) (cannot be answered without knowing the tangent lengths)
Solution:
(C) equal to

Explanation: XM = XA … (i)
and YM = YB … (ii)
(∵ Tangents drawn from an external point to a circle are equal)
Now, In APXY
Perimeter of ΔPXY = PX + XY + YP
= PX + XM + MY + YP
(∵ XV = XM + MY)
From (i) and (ii) we get
= PX + XA + YB + YP
Thus perimeter of ΔPXY = PA + PB
(∵ PX + XA = PA
YB + YP = PB)
Hence, perimeter of APXY is equal to the sum of tangents PA and PB.

Question 10.
The non-zero value of k for which the quadratic equation 3x² – kx + k = 0 has equal roots, is [1]
(a) 10
(b) 11
(c) 12
(d) 14
Answer:
(c) 12

Given, the quadratic equation is 3x² – kx + k = 0.
On comparing with ax² + bx + c = 0, we get
a = 3,b = -k and c = k
Condition for equal roots,
b² – 4ac = 0
⇒ (- k)² – 4 × 3 × k = 0
⇒ k(k – 12) = 0 ⇒ k = 0,12
Hence, the non-zero value of k is 12.

Question 11.
If cos y = 0, then what is the value of \(\frac{1}{2}\) cos \(\frac{y}{2}\)
(A) 0
(B) \(\frac{1}{2}\)
(C) \(\frac{1}{\sqrt{2}}\)
(D) \(\frac{1}{2 \sqrt{2}}\)
Solution:
(D) \(\frac{1}{2 \sqrt{2}}\)

Explanation: cos y = 0 (Given)
We know that, cos 90° = 0
∴ cos y = cos 90°
So, y = 90°
Putting value of y in \(\frac{1}{2}\) cos \(\frac{y}{2}\), we get
\(\frac{1}{2}\) cos \(\frac{90°}{2}\) = \(\frac{1}{2}\) cos 45°
= \(\frac{1}{2}\) × \(\frac{1}{\sqrt{2}}\) [∵ cos 45° = \(\frac{1}{\sqrt{2}}\)]
= \(\frac{1}{2 \sqrt{2}}\)

Question 12.
The probability of passing a certain test is \(\frac{x}{24}\). If the probability of not passing is \(\frac{7}{8}\) then x is equal to [1]
(a) 2
(b) 3
(c) 4
(d) 6
Answer:
(a) 2

Let E be the event of passing the test, P(E) = \(\frac{x}{24}\)
Also, P (not passing the test), \(P(\bar{E})\) = \(\frac{7}{8}\)
Now, P(E) + \(P(\bar{E})\) = 1
\(\frac{x}{24}\) + \(\frac{7}{8}\) = 1 ⇒ \(\frac{x}{24}\) = 1 – \(\frac{7}{8}\)
⇒ \(\frac{x}{24}\) = \(\frac{8-7}{8}\) ⇒ \(\frac{x}{24}\) = \(\frac{1}{8}\)
⇒ x = \(\frac{24}{8}\)
⇒ x = 3

Question 13.
A 9 m high street light pole is broken during a storm. The top end of the pole touches the ground at 30°. At what height did the pole breaks?
(A) 3 m
(B) 3.75 m
(C) 4.5 m
(D) 9 m
Solution:
(A) 3 m

Explanation: Let the height of Pole = BD = 9 m
Pole is broken at point C
So, let AC = CD = x m
And BC = (9 – x) m

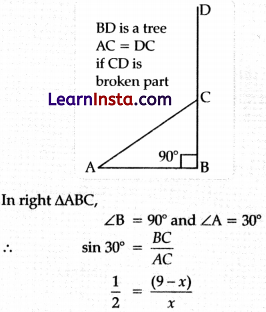
x = 18 – 2x
x + 2x = 18
3x = 18
x = 6m
Thus, BC = 9 – 6 = 3m
∴ Pole break at height of 3 m.

Question 14.
The area of shaded portion is [1]

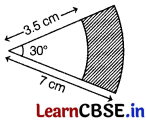
(a) 9.625 cm²
(b) 6.925 cm²
(c) 9 cm²
(d) 6 cm²
Answer:
(a) 9.625 cm²

Required area
= Area of sector of angle 30° with radius 7 cm – Area of sector of angle 30° with radius 3.5 cm
= \(\left(\frac{30^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 7^2\right)\) – \(\left(\frac{30^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 3.5^2\right)\)
= \(\frac{77}{6}-\frac{77}{24}\) = \(\frac{77}{24}\) × 3 = \(\frac{77}{8}\) = 9.625 cm²

Question 15.
In the figure given below, O is the centre of the circle, PR and RQ are chords of the circle. The radius of the circle is 5 cm. PR = 8 cm, QR = 6 cm and ∠PRQ = 90°.

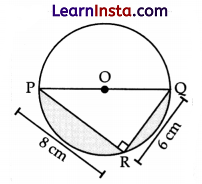
(Note: The figure is not to scale.)
What is the approximate are of the shaded region?
(A) \(\left(\frac{25}{4} \pi-24\right)\)
(B) \(\left(\frac{25}{2} \pi-24\right)\)
(C) \(\left(\frac{25}{4} \pi\right)\)
(D) \(\left(\frac{25}{2} \pi\right)\)
Solution:
(B) \(\left(\frac{25}{2} \pi-24\right)\)

Explanation: Area of semicircle with radius 5 cm

Question 16.
The mean and median of a distribution are 14 and 15, respectively. The value of mode is [1]
(a) 16
(b) 17
(c) 13
(d) 18
Answer:
(b) 17

Given, mean = 14 and median = 15
By using empirical relationships,
Mode = 3 Median -2 Mean
= 3 × 15 – 2 × 14 = 45 – 28 = 17

Question 17.
Two dice are rolled simultaneously. What is the probability that 6 will come up at least once?
(A) \(\frac{1}{6}\)
(B) \(\frac{7}{36}\)
(C) \(\frac{11}{36}\)
(D) \(\frac{13}{36}\)
Solution:
(C) \(\frac{11}{36}\)

Explanation: Total possible outcomes, when two dice are thrown together = 6 × 6
i.e., n(S) = 36
Favourable outcomes are (1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
∴ n(E) = 11
i.e., P(6 will come up at least once) = \(\frac{n(E)}{n(S)}\)
= [\(\frac{11}{36}\)

Question 18.
If point C(k, 4) divides the join of points A(2,6) and 5(5,1) in the ratio 1 : 3, then the value of k is ? [1]
(a) 11
(b) \(\frac{29}{4}\)
(c) \(\frac{11}{4}\)
(d) \(\frac{9}{4}\)
Answer:
(c) \(\frac{11}{4}\)

Given, a line joining points A (2, 6) and B (5,1) is
divided by point C in 1 : 3.
AC : BC = 1 : 3
Thus, the x-coordinate of the point C is given by
k = \(\frac{3 \times 2+1 \times 5}{1+3}\) = \(\frac{6+5}{4}\) = \(\frac{11}{4}\)

DIRECTIONS: Two statements are given below – one labelled Assertion (A) and the other labelled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).
(A) Both (A) and (R) are true and (R) is the correct explanation of the (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation of the (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.

Question 19.
Assertion (A): In a right circular cone, the cross-section made by a plane parallel to the base is a circle.
Reason (R): If the volume and the surface area of a solid hemisphere are numerically equal, then the diameter of hemisphere is 9 units.
Solution:
(B) Both (A) and (R) are true but (R) is not the correct explanation of the (A).

Explanation: In case of assertion:
In a right circular cone, if any cut is made parallel to its base, we get a circle.
∴ Assertion is true.
In case of reason:
Let radius of sphere be r.
Given; volume of hemisphere = Surfacearea ofhemisphere
or, \(\frac{2}{3}\)πr³ = 3πr²
or, r = \(\frac{9}{2}\) units
∴ Diameter = \(\frac{9}{2}\) × 2 = 9 units
Reason is also true.
Hence, Assertion and Reason both are true. But Reason is not an explanation of Assertion.

Question 20.
Assertion (A): If LCM =182, product of integers is 26 × 91, then HCF = 13.
Reason (R): LCM × Product of integers = HCF [1]
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(c) Assertion (A) is true but Reason (R) is false.

We know, LCM × HCF = Product of two numbers
⇒ 182 × HCF = 26 × 91
⇒ HCF = \(\frac{26 × 91}{182}\) = 13
∴ Hence, Assertion (A) is true but Reason (R) is false.

Section – B (10 Marks)
Section B consists of 5 questions of 2 marks each.

Question 21.
M and N are positive integers such that M = p²q³r and N = p³q², where p, q, r are prime numbers.
Find LCM (M, N) and HCF (M, N)
Solution:
M = p²q³r
N = p³q²
∴ LCM(M, N) = p³q³r
HCF (M, N) = p²q²

Question 22.
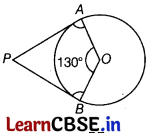
If two tangents inclined at an angle of 60° are drawn to a circle of radius 5 cm, then find the length of each tangent.
Or
In the given figure, if the angle between two radii of a circle is 130°, then find the angle between the tangents at the ends of the radii. [2]

Solution:
In the given figure, OA = 5 cm and ∠APB = 60°

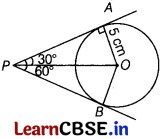
In ∆APO, ∠PAO = 90°
[∵ the tangent at any point of a circle is perpendicular to the radius through the point of contact]
Since, ∠APB = 60°
⇒ ∠APO= \(\frac{60°}{2}\) = 30°
[∵ ∆OAP ≅ ∆OBP ⇒ ∠OPA = ∠OPB]
∴ tan 30° = \(\frac{A O}{A P}\) ⇒ \(\frac{1}{\sqrt{3}}=\frac{5}{A P}\)
⇒ AP = 5√3 cm
Hence, the length of each tangent is 5√3 cm.

Or

From figure, ∠AOB = 130° … (i)
Clearly, ∠PAO = ∠PBO = 90° … (ii)
[∵ radius is perpendicular to the tangent at the point of contact]
Now, applying angle sum property of quadrilateral in OAPB, we have
∠PAO + ∠AOB + ∠OBP + ∠APB = 360°
⇒ 90° +130° + 90 °+ ∠APB = 360° [from Eqs. (i) and (ii)]
∴ ∠APB = 360° – 310° = 50°
Hence, the angle between the tangent at the ends of the radii is 50°.

Question 23.
If AB is a tangent drawn from a point A to a circle with centre O and BOC is a diameter of circle such that ∠AOC = 105°, then find ∠OAB.
Solution:
Given, AB and BOC are the tangent and diameter of the circle with centre O, respectively.
We know that, tangent at any point on a circle is perpendicular to the radius through the point of contact.
∴ OB ⊥ AB
⇒ ∠OBA = 90°
∠AOC = 105°

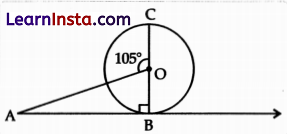
In ΔABO,
∠AOC = ∠OAB + ∠OBA
[∵ External angle = Sum of opposite internal angles]
⇒ 105° = ∠OAB + 90°
⇒ ∠OAB = 105° – 90°
⇒ ∠OAB = 15°

Question 24.
If tan(A + B) = √3 and tan (A – B) = \(\frac{1}{\sqrt{3}}\). 0° < A + B ≤ 90°, A >B, then find A and B.
Or
If cosec A = √2, then find the value of \(\frac{2 \sin ^2 A+3 \cot ^2 A}{4 \tan ^2 A-\cos ^2 A}\). [2]
Solution:
We have, tan (A + B) = √3
⇒ tan (A + B) = tan 60° [∵ tan 60° = √3]
∴ A + B = 60° ……….(i)
and tan (A – B) = \(\frac{1}{\sqrt{3}}\)
⇒ tan (A – B) = tan 30° [∵ tan 30° = \(\frac{1}{\sqrt{3}}\)]
∴ A – B = 30° ……….(ii)
On adding Eqs. (i) and (ii), we get
A + B + A – B = 60°+ 30°
⇒ 2A = 90°
⇒ A = 45°
On putting, A = 45° in Eq. (i), we get
45° + B = 60°
∴ B = 60° – 45° = 15°
Hence, A = 45° and B = 15°.

Or

We have, cosec A = √2
⇒ cosec A = cosec 45° ⇒ A = 45°

Question 25.

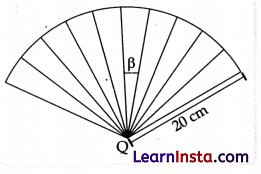
(A) The figure below is a part of a circle with centre O. Its area is \(\frac{1250 \pi}{9}\) cm² and the 10 sectors are identical.
(Note: The figure is not to scale)
Find the value of p, in degrees. Show your steps
Solution:

= 12.5°
Thus, value of β = 12.5°

OR

(B) Avikant bought a pair of glasses with wiper blades. He was curious to know the area being cleaned by each of the wiper blades. With the help of a ruler and a protractor, he found the length of each blade as 3 cm and the angle swept as 60°.
Solution:

(Note: The figure is for visual representation only)
(i) Find the area that each wiper cleans in one swipe, in terms of n.
(ii) If the diameter of each circular glass is 5 cm, what percent of the area of the glass will be cleaned by the blade in one swipe?
Show your work.
Solution:

Section – C (18 Marks)
Section C Consists of 6 questions of 3 marks each

Question 26.
Prove that 5√2 is irrational. [3]
Solution:
Let us assume that 5√2 is a rational number.
Then, there exist coprime positive integers a and b such that
5√2 = \(\frac{a}{b}\)
⇒ √2 = \(\frac{a}{5b}\)
∵ 5 a and feare integers, so \(\frac{a}{5b}\) is a rational number.
⇒ √2 is a rational number.
But this contradicts the fact that √2 is irrational. So, our assumption is not correct.
Hence, 5√2 is an irrational number.

Question 27.
If one root of the quadratic equation 3x² + px + 4 = 0 is  \(\frac{2}{3}\), then find the value of p and the other root of the equation.
Solution:
3x² + px + 4 = 0
∵ \(\frac{2}{3}\) is a root so it must satisfy the given equation
3(\(\frac{2}{3}\)) + p(\(\frac{2}{3}\)) + 4 = 0
\(\frac{4}{3}\) + \(\frac{2p}{3}\) + 4 = 0
On solving, we get
p = -8
3x² – 8x + 4 = 0
3x² – 6x – 2x + 4 = 0
3x(x – 2) – 2(x – 2) = 0
x = \(\frac{2}{3}\) or x = 2
Hence, x = 2
So the other root is 2.

Question 28.
Show graphically that the following system of equations is inconsistent i.e. it has no solution 3x – Ay -1 = 0 and 2x – \(\frac{8}{3}\) y + 5=0. [3]
Solution:
We have, 3x – 4y -1 = 0
and 2x – \(\frac{8}{3}\) y + 5 = 0
Table for equation 3x – 4y -1 = 0 ⇒ y = \(\frac{3x-1}{4}\)

Now, we plot all these points on a graph paper and join them.
Table for equation 2x – \(\frac{8}{3}\) y + 5 = 0
⇒ 6x – 8y + 15= 0
⇒ y = \(\frac{6x+15}{8}\)

x	0	-2.5	1.5
y	1.875	0	3
Points	D(0, 1.875)	E(-2.5, 0)	F(1.5,3)

Now, we plot all these points on a graph paper and join them.

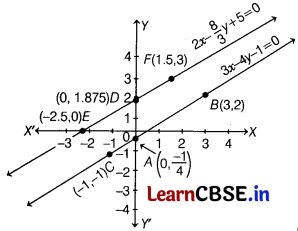
So, the two lines have no common point. Hence, the given system of equations is inconsistent.

Question 29.
(A) Given below is the diagram of pair of pulleys.

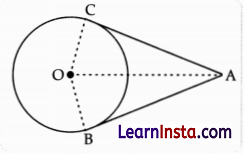
The length of AC is 12 cm.
In the given figure, ∠CAB = 20°.
What is the measure of ∠AOC?
Solution:
Angle between two tangents = 20°
As tangents are equally inclined to each other.
∴ ∠CAO = ∠BAO = 10°
Now, In ΔAOC
∠CAO +  ∠AOC + ∠ACO = 180°
Here, ∠ACO = 90°
(Tangent at any point of a circle is perpendicular to the radius through the point of contact.)
So, 10° + 90° + ∠AOC = 180°
∴ ∠AOC = 180° – 100°
= 80°
Hence ∠AOC = 80°.

(B) In given figure, two circles touch each other at the point C. Prove that the common tangent to the circles at C, bisects the common tangent at P and Q.

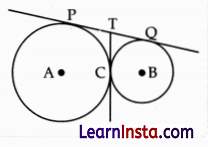
Solution:
Since, PT = TC
⇒ QT = TC
[Tangents of circle from external point]
So, PT = QT
Now PQ = PT + TQ
⇒ PQ = PT + PT
⇒ PQ = 2PT
⇒ \(\frac{1}{2}\) PQ = PT
Hence, the common tangent to the circle at C bisects the common tangents at P and Q.

Question 30.
If a and p are the zeroes of the quadratic polynomial f(x) = 3x² – 5x – 2, then find the value of α³ + β³. [3]
Solution:
Given, a and p are the zeroes of a quadratic polynomial.
f(x) = 3x² – 5x – 2
On comparing with f(x) = ax² + bx + c, we get
a = 3, b = – 5 and c = – 2
We know that
α + β = \(\frac{b}{a}\) = \(\frac{-(-5)}{3}\) = \(\frac{5}{3}\)
and = \(\frac{c}{a}\) = \(-\frac{2}{3}\)
∴ α³ + β³ = (α + β) (α² – α . β + β²)
= (α + β) [(α + β)² – 3α . β]
= \(\frac{5}{3}\)[(\(\frac{b}{a}\))² – 3 × (\(-\frac{2}{3}\))]
= \(\frac{125}{27}\) + 2 × \(\frac{5}{3}\)
= \(\frac{125+90}{27}\) = \(\frac{215}{27}\)

Question 31.
Arti owns a manufacturing company. She hires 5 supervisors and 20 operators of a 6-months project. The table given below shows their salary breakup.

Position	Salary for the two months	Salary for the remaining four months
Supervisor	Between ₹18,000 to ₹20,000	Between ₹22,000 to ₹25,000
Operator	Between ₹8,000 to ₹10,000	Between ₹13,000 to ₹15,000

The mean salary of five supervisors for the first two months is ₹19,000.
The salary of three supervisors are ₹18,000, ₹18,500 and ₹20,000 respectively. Find the sum of other two supervisor’s salary for first two months.
Solution:
Mean salary of 5 supervisors for first two months = ₹19,000

⇒ 56,500 + 2 supervisor’s salary = 95,000
Hence, 2 supervisor’s salary = 95,000 – 56,500
= ₹38,500

Section – D (20 Marks)
Section D consists of 4 questions of 5 marks each

Question 32.
Find the nature of roots of the following quadratic equations. In case real roots exist, find them
(i) 4x² + 12x + 9 = 0
(ii) 3x² + 5x – 7 = 0 [5]
Solution:
(i) Given, quadratic equation is
4x² + 12x + 9 = 0
On comparing with ax² + bx + c = 0, we get
a = 4, b = 12 and c = 9
Now, D = b² – 4ac
= (12)² – 4 (4) (9)
= 144 – 144 = 0
Since, D = 0, so given quadratic equation has two equal and real roots which are given by
x = \(\frac{-b \pm \sqrt{D}}{2 a}\) = \(\frac{-12 \pm 0}{2(4)}\)
⇒ x = \(\frac{-12+0}{8}\)
or x = \(\frac{-12-0}{8}\)
⇒ x = \(-\frac{3}{2}\) or x = \(-\frac{3}{2}\)
Hence, the roots are \(-\frac{3}{2}\) and \(-\frac{3}{2}\).

(ii) Given, quadratic equation is
3x² + 5x – 7 = 0
On comparing with ax² + bx + c = 0, we get
a = 3, b = 5 and c = – 7
Now, D = b² – 4ac = (5)² – 4(3) (-7)
= 25 + 84=109
Since, D > 0, so given quadratic equation has two distinct real roots which are given by
x = \(\frac{-b \pm \sqrt{D}}{2 a}\) = \(\frac{-5 \pm \sqrt{109}}{2(3)}\)
⇒ x = \(\frac{-5 + \sqrt{109}}{6}\) [taking positive sign]
or x = \(\frac{-5 – \sqrt{109}}{6}\) [taking negative sign]
Hence, the roots are \(\frac{-5 + \sqrt{109}}{6}\) and \(\frac{-5 – \sqrt{109}}{6}\).

Question 33.
Shown below is circle with centre O. YX is tangent to the circle at Y.

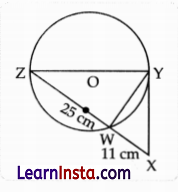
(Note: The figure is not to scale.)
(i) Prove that ΔZWY – ΔZYX.
(ii) Using part (i), find the length of ZY.
Show your steps and give valid reasons.
Solution:
(i) In ΔXYZ
∠ZYX = 90°
(∴ Tangent at any point of a circle is perpendicular to the radius through the point of contact.)
In ΔWYZ
∠ZWY = 90° (Angle is semicircle is right angle)
In ΔXYZ and ΔWYZ
∠ZYX = ∠ZWY = 90°
(Proved Above)
∠Z = ∠Z (common)
ΔXYZ ~ ΔWYZ
(By AA similarity criterion)

(ii) In ΔXYZ and ΔWYZ
\(\frac{Z X}{Z Y}\) = \(\frac{Z Y}{Z W}\)
(In similar triangles the ratio of their corresponding sides are equal.)
\(\frac{25+11}{Z Y}\) = \(\frac{Z Y}{25}\)
36 × 25 = ZY²
6 × 5 = ZY
∴ ZY = 30 cm

Question 34.
The weights (in kg) of 50 wrestlers are recorded in the following table.

Weight (in kg)	Number of wrestlers
100-110	4
110-120	14
120-130	21
130-140	8
140-150	3

Find the mean weight of the wrestlers.
Or
If mode of the following series is 54, then find the value of f.

Class interval	0-15	15-30	30-45	45-60	60-75	75-90
Frequency	3	5	f	16	12	7

Find the modal class in which the given mode lies and find the value of f. [5]
Solution:
We first find the class mark x, of each class and then proceed as follows

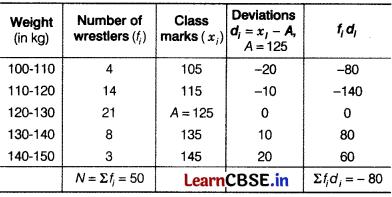
Here, Assumed mean (A) = 125,
Class width (h) = 10
and total observation (N) = 50
By assumed mean method,
Mean (x) = A + \(\frac{\Sigma f_i d_i}{\Sigma f_i}\)
= 125 + \(\frac{(-80)}{50}\) = 125 – 1.6
= 1234 kg

Or

Here, given mode is 54, which lies between 45-60.
Therefore, the modal class is 45-60.
l = 45, f₁ = 16, f₀ = f, f₂ = 12 and h = 15
∴ Mode = l + \(\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right)\) × h
54 = 45 + \(\left(\frac{16-f}{2(16)-f-12}\right)\) × 15
⇒ 9 = \(\frac{16-f}{20-f}\) × 15
⇒ 9(20 – f) = 15(16 – f)
⇒ 180 – 9f = 240 – 15f
⇒ 6f = 240 – 180 = 60
⇒ f = 10
Hence, the required value of f is 10.

Question 35.
For the table given below, answer the following questions.

Salary (in ₹)	Number of operators
₹13,000	5
₹13,500	3
₹14,000	2
₹14,500	4
₹15,000	6

(i) What is the median salary of the operators?
Solution:

= ₹14,250
Median salary of the operators = ₹14,250

(ii) What is the salary received by most of the operators?
Solution:
Salary received by most of the operators = ₹15000

Section – E (12 Marks)
Case study based questions are compulsory.

Question 36.
Spinning Wheel Game
A game of chance consists of spinning an arrow that comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8 (see figure) and these are equally likely outcomes.

Based on the above information, answer the following questions.
(i) Find the probability that the arrow point lies on the number 8. [1]
(ii) What is the probability that arrow point lies on an odd number? [2]
Or
What is the probability that it will point at a number greater than 2? [2]
(iii) Find out the probability that the pointer lies on 9. [1]
Solution:
∵ Total number of points on the circle = 8
(i) Let E₁= Event of getting arrow at number 8.
∴ Number of outcomes favourable to E₁ = 1
Probability that arrow points at number 8,
P(E₁) = \(\frac{\text { Outcomes favourable to E_1 }}{\text { Total number of outcomes }}\)
= \(\frac{1}{8}\)

(ii) Let E₂ = Event of getting arrow at an odd number
Here, odd numbers are 1, 3, 5 and 7.
∴ Number of outcomes favourable to E₂ = 4

Probability that arrow points at an odd number,
P(E₂) = \(\frac{\text { Outcomes favourable to E_2 }}{\text { Total number of outcomes }}\)
= \(\frac{4}{8}\) = \(\frac{1}{2}\)
Let E₃ = Event of getting arrow at a number greater than 2, i.e. at 3, 4, 5,6,7 and 8
∴ Number of outcomes favourable to E₃ = 6
Probability that arrow points at a number greater than 2,
P(E₃) = \(\frac{\text { Outcomes favourable to E_3 }}{\text { Total number of outcomes }}\)
= \(\frac{6}{8}\) = \(\frac{3}{4}\)

(iii) Let E₄ = Event of getting arrow at number 9.
∴ Number of outcomes favourable to E₄ = 0
Probability that arrow points at number 9.
P(E₄) = \(\frac{\text { Outcomes favourable to E_3 }}{\text { Total number of outcomes }}\)
= \(\frac{0}{8}\) = 0

Question 37.

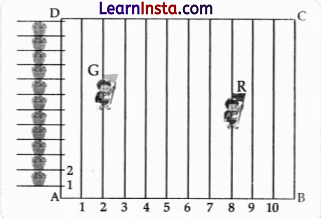
To conduct Sports Day activities in your School, lines have been drawn with chalk powder at a distance of 1 m each, in a rectangular shaped ground ABCD, 100 flowerpots have been placed at a distance of1 m from each other along AD, as shown in given figure below. Niharika runs 1/4^th the distance AD on the 2nd line and posts a green (G) flag. Preet runs 1/5^th distance AD on the eighth line and posts a red (R) flag.
(i) Find the position of green flag?
(ii) Find the position of red flag?
(iii) What is the distance between both the flags?
Solution:
(i) As Niharika runs \(\frac{1}{4}\)th distance of AD = y coordinate
= \(\frac{1}{4}\) × 100 = 25
And, x coordinate = 2
∴ Position of green flag = (2, 25)

(ii) As Preet runs l/5th distance of AD = y coordinate
= \(\frac{1}{5}\) × 100 = 20
And, x coordinate = 8
∴ position of red flag = (8, 20)

(iii) Distance between both the flags

OR

If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, Where should she post her flag?
Solution:
According to mid point formula

Question 38.
Beehive
A beehive is an enclosed cell structure in which some honeybee species of the subgenus Apis live and raise their young. Each cell is in the shape of a hexagon.
In a regular hexagon, there are six edges of equal lengths. Take O as centre and join all the vertices from the centre.

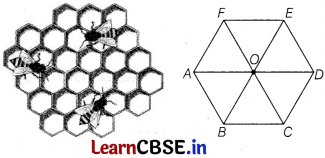
Similarity of Triangle
Two triangles are said to be similar if their all corresponding angles are equal and all corresponding sides are proportional. Based on the above information, answer the following questions.
(i) Find the number of equilateral triangles in the given figure. [1]
(ii) If the area of two triangles is equal, then they are always congruent or not. [1]
(iii) How many triangles are similar in the given figure? [2]
Or
Find the area of the hexagon, if each edge is of length a. [2]
Solution:
(i) Total number of equilateral triangles in the given figure is 6.
(ii) If the area of two triangles is equal, then they are always congruent.
(iii) As we know there are six equilateral triangles all having equal sides.
Hence, we get six similar triangles.
Or
Area of hexagon
= 6 × Area of one equilateral triangle having side a
= 6 × \(\frac{\sqrt{3}}{4}\) × (a)²
= \(\frac{3 \sqrt{3}}{2}\) (a)² sq units.