Students can access the CBSE Sample Papers for Class 10 Maths Basic with Solutions and marking scheme Set 4 will help students in understanding the difficulty level of the exam. BEL Pivot Point Calculator
CBSE Sample Papers for Class 10 Maths Basic Set 4 with Solutions
Maximum Marks: 80
Time Allowed: 3 hours
General Instructions:
1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying1 mark each.
3. Section B has 5 Short Answers-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answers-IT (SA-II) type questions carrying 3 marks each
5. Section D has 4 Long Answers (LA) type questions carrying5 marks each.
6. Section E has 3 source based/case based/passage based integrated units of assessment (4 marks each) with sub¬ parts of the values of 1,1 and 2 marks each respectively.
7. All questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Qs of 5 marks has been given provided. An internal choice has been provided in 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7, wherever required if not stated.
Section – A(20 Marks)
Question 1.
LCM of smallest prime and smallest composite number is :
(A) 1
(B) 2
(C) 3
(D) 4
Solution:
(D) 4
Explanation: We know that,
Smallest prime number = 2
Smallest composite number = 4
LCM (2,4) = 4
Question 2.
√2 – √B is
(A) Rational Number
(B) Integer
(C) Irrational Number
(D) None of these
Solution:
(C) Irrational Number
Explanation: We know that J2 and J3_ both are irrational numbers and the Difference between two irrational numbers is always irrational.
Question 3.
If x = 3 is one of the roots of the quadratic equation x2 – 2kx – 6 = 0, then the value of k is: 1
(a) –\(\frac{1}{2}\)
(b) \(\frac{1}{2}\)
(c) 3
(d) 2
Answer:
(b) \(\frac{1}{2}\)
Explanation: Given one root of x2 – 2kx – 6 = 0
is x = 3
Putting x = 3 in the above quadratic eqn., we get
(3)2 – 2k × 3 – 6 = 0
9 – 6k – 6 = 0
-6k = 6 – 9
-6k = – 3
k = \(\frac{-3}{-6}=\frac{1}{2}\)
Hence, the value of k = \(\frac{1}{2}\)
![]()
Question 4.
The quadratic equation 2x2 – √5x + 1 = 0 has
(A) two distinct real roots
(B) two equal real roots
(C) no real roots
(D) more than 2 real roots
Solution:
(C) no real roots
Explanation : 2x2 – √5x + 1 = 0
On comparing with ax2 + bx + c =0
a = 2,b = -√5, c = 1
Discriminant = b2 – 4ac = (-√5)2 – 4(2)(1)
= 5 – 8 = -3 < 0
Therefore, the equation has no real roots.
Question 5.
Graphically, the pair of equations x = 9 and y = 17 represents two lines which are
(A) intersecting at (17, 9)
(B) intersecting at (9, 17)
(C) coincident
(D) parallel
Solution:
(B) intersecting at (9, 17)
Explanation : Given equations are x = 9, y = 17 in standard form x + 0 .y – 9 = 0 and 0.x + y – 17 = 0
\(\begin{aligned}
& \frac{a_1}{a_2}=\frac{1}{0}, \frac{b_1}{b_2}=\frac{0}{1} \\
& \frac{c_1}{c_2}=\frac{-9}{-17}=\frac{9}{17}
\end{aligned}\)
Since, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
Hence, given lines are intersecting at x = 9, y = 17
ie., (9,17)
Question 6.
If 2 sin 3θ = √3, then the value of θ is
(a) 60°
(b) 30°
(c) 20°
(d) 15°
Answer:
(c) 20°
we have, 2 sin 3θ = √3
⇒ sin 3θ = \(\frac{\sqrt{3}}{2}\)
⇒ sin 3θ = sin 60°
⇒ θ = \(\frac{60^{\circ}}{3}\)
∴ θ = 20°
Question 7.
In the given figure, if TP and TQ are tangents to a circle with centre O, so that ∠POQ = 110°, then ∠PTQ is
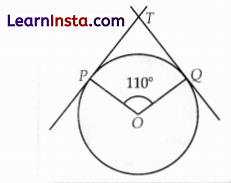
(A) 110°
(B) 90°
(C) 80°
(D) 70°
Solution:
(D) 70°
Explanation: Given, ∠POQ = 110°
Since, the tangent at any point of a circle is perpendicular to the radius through the point of contact
∠OPT = 90°, ∠OQT = 90°
Now i in quadrilateral ∠PTQ, ∠POQ + ∠OQT + ∠QTP + ∠TPO = 360°
110° + 90° + ∠QTP + 90° = 360°
∠QTP = 70°
Question 8.
In the figure given below, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3.cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to
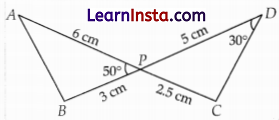
(A) 50°
(B) 30°
(C) 60°
(D) 100°
Solution:

(D) 100°
In the given figure, PB \(\frac{P A}{P B}=\frac{6}{3}\) = 2 and \(\frac{P D}{P C}=\frac{5}{2.5}\) = 2
Thus, in ΔAPB ∼ ΔDPC,
and ∠APB = ∠DPC (vertically opposite angle)
By SAS similarity, we get ΔAPB ∼ ΔDPC.
∠PAB = ∠PDC = 30°
Now in Triangle APB,
∠PAB + ∠PBA + ∠APB = 180° (Angle sum property of triangle)
30 + ∠PBA + 50 = 180
∠PBA = 100
Hence, ∠PBA = 100°.
![]()
Question 9.
In figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to: 1

(a) 60°
(b) 70°
(c) 80°
(d) 90°
Answer:
(b) 70°
Explanation: Given that ∠POQ = 110°
∠OQT = ∠OPT = 90°
[∵ A tangent at any point of a circle is perpendicular to the radius at any point of contact]
Also, ∠TQO + ∠QOP + ∠OPT + ∠PTQ = 360°
[Sum of all angles of a quadrilateral is 360°]
∠PTQ = 360° – 90° – 90° – 110°
∠PTQ = 70°
Question 10.
Given that sec θ = √2, the value of is
(A) 2√2
(B) √2
(C) 3√2
(D) 2
Solution:
(A) 2√2
Explanation: It is given that
sec θ = √2 …(i)
Also, sec 45° = √2 …(ii)
From (i) and (ii), we get
θ = 45°
Put value of θ in \(\frac{1+\tan \theta}{\sin \theta}\),
\(\frac{1+\tan \theta}{\sin \theta}=\frac{1+\tan 45^{\circ}}{\sin 45^{\circ}}\)
\(=\frac{1+1}{\frac{1}{\sqrt{2}}}\)
Or, = 2 √2
Question 11.
1f 4 tan θ = 3, then \(\left(\frac{4 \sin \theta-\cos \theta}{4 \sin \theta+\cos \theta}\right)\) is equal to
(A) \(\frac{1}{3}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{1}{2}\)
(D) \(\frac{3}{4}\)
Solution:
(C) \(\frac{1}{2}\)

Question 12.
The coordinates of the point which divides the line segment joining the points (4, – 3) and (8, 5) in the ratio 1 : 3 internally are
(a) (4, 3)
(b) (7, 3)
(c) (3, 5)
(d) (5, – 1)
Answer:
(d) (5, – 1)
Let (x1, y1) = (4, – 3)
and (x2, y2) = (8, 5)
Let (x, y) be the coordinates of the point which divides the line joining the points (x1, y1) and (x2, y2) in ratio m : n = 1 : 3 internally.
So, (x, y) = \(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)\)
= \(\left(\frac{1(8)+3(4)}{1+3}, \frac{1(5)+3(-3)}{1+3}\right)\)
= \(\left(\frac{20}{4}, \frac{-4}{4}\right)\)
= (5, – 1)
Question 13.
The total surface area of a solid hemisphere of radius 7 cm is
(A) 4477 cm2
(B) 2392 cm2
(C) 174 cm2
(D) 147n cm2
Solution:
(D) 147n cm2
Explanation: Radius of a hemisphere (r) =7cm
∴ Total surface area of a solid hemisphere
= 3πr2
= 3π(7)2
= 147π cm2
![]()
Question 14.
The diameter of a car wheel is 42 cm. The number of complete revolutions it will make in moving 132 km is
(A) 104
(B) 105
(C) 106
(D) 103
Solution:
(B) 105

Question 15.
When a dice is thrown once, the probability of getting an even number less than 4 is: 1
(a) \(\frac{1}{4}\)
(b) 0
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{6}\)
Answer:
(d) \(\frac{1}{6}\)
Explanation: When a die is thrown the possible outcomes are 1, 2, 3, 4, 5, and 6.
favourable outcomes (even number Less than 4) is 2.
So, total number of favourable outcomes is 1.
P (even number less than 4) = \(\frac{1}{6}\)
Question 16.
While computing mean of grouped data, we assume that the frequencies are
(A) evenly distributed over all the classes
(B) centred at the class marks of the classes
(C) centred at the upper limits of the classes
(D) centred at the lower limits of the classes
Solution:
(B) centred at the class marks of the classes
Explanation: In grouping the data from ungrouped data, all the observations between lower and upper limits of class marks are taken in one group then mid-value or class mark is taken for further calculation.
Therefore, frequencies or observations must be centred at the class marks of the classes.
Question 17.
A plumbline (Sahul) is the combination of

(A) a cone and a cylinder
(B) a hemisphere and a cone
(C) frustum of a cone and a cylinder
(D) sphere and cylinder
Solution:
(B) a hemisphere and a cone
Question 18.
The discriminant of the quadratic equation 6x2 – 7x + 2 = 0 is
(a) \(\sqrt{41}\)
(b) \(\frac{1}{12}\)
(c) 5
(d) None of these
Answer:
(d) None of these
Given, 6x2 – 7x + 2 = 0 …………..(i)
On comparing Eq. (i) with ax2 + bx + c = 0, we get
a = 6, b = -7 and c = 2
We know that D = b2 – 4ac = (- 7)2 – 4 (6) (2)
= 49 – 48 = 1
Hence, the value of the discriminant is 1.
Directions: A Statement of Assertion (A) is followed by a statement of Reason (R) in the following questions. Mark the correct choice as.
Question 19.
Assertion (A): The ratio in which the line segment joining (2, -3) and (5, 6) internally divided by x-axis is 1: 2.
Reason (R): As the formula for the internal division is \(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)\)
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A)is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
Explanation: For assertion,
Let the required point be P(a, 0) and required ratio
AP: PB = k: 1.
Using section formula,

![]()
Question 20.
Assertion (A): (7 × 13 × 11) + 11 and (7 × 6 × 5 × 4 × 3 × 2 ×1) +3 have exactly composite numbers.
Reason (R): (3 × 12 × 101) + 4 is not a composite number.
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
(C) (A) is true but (R) is false.
Explanation: 7 × 3 × 11 + 11 can be written as 11(7 × 3 + 1)
Therefore, it is a multiple of 11 which makes this number as composite number.
Similarly,7 × 6 × 5 × 4 × 3 × 2 × 1 + 3 is a multiple of 3 which makes this number also a composite number.
Also, 3 × 12 × 101 + 4 is a multiple of 4.
Therefore, A is true but R is false.
Section – B(10 Marks)
Question 21.
Find whether the following pair of linear equations is consistent or inconsistent: 2
3x + 2y = 8
6x – 4y = 9
Answer:
3x + 2y = 8
6x – 4y = 9
a1 = 3, b1 = 2, c1 = 8
a2 = 6, b2 = -4, c2 = 9
\(\frac{a_1}{a_2}=\frac{3}{6}=\frac{1}{2} \quad \frac{b_1}{b_2}=\frac{2}{-4}=\frac{-1}{2}\) and \(\frac{c_1}{c_2}=\frac{8}{9}\)
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
The given pair of linear equations is consistent
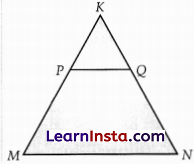
Question 22.
In the figure, PQ is parallel to MN. If \(\frac{K P}{P M}=\frac{4}{13}\) and KN = 20.4 cm, then find KQ.
Solution:
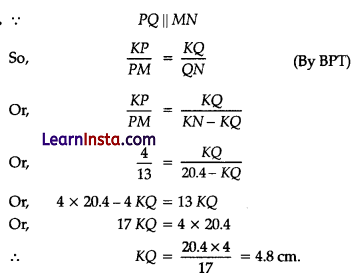
OR
In the figure, quadrilateral ABCD is circumscribing a circle with centre O and AD ⊥ AB. If radius of in-circle is 10 cm, then find the value of x.
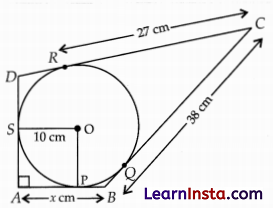
Solution:
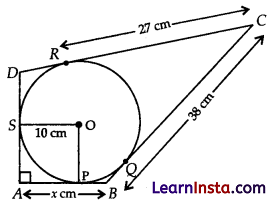
∠A = ∠OPA = ∠OSA = 90°
Hence, ∠SOP = 90°
Also, AP = AS
Tangent drawn from an external point to a circle are equal)
Hence, OSAP is a square.
AP = AS = 10cm
CR =CQ=27cm
(Tangent drawn from an external point to a circle are equal)
BQ = BC – CQ
= 38 – 27 = 11cm
BP = BQ = 11cm
(Tangent drawn from an external point to a circle are equal)
x = AB = AP + BP
= 10 + 11 = 21 cm
Question 23.
In fig., PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.
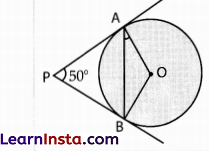
Solution:
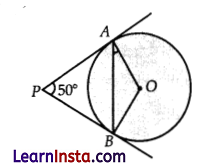
Here, ∠APB = 50°
(Tangent drawn from an external point to a circle are equal, therefore PA = PB)
∠PAB = ∠pBa = \(\frac{180^{\circ}-50^{\circ}}{2}\)
= 65°
(Angles opposite to equal sides are equal )
∠OAB = 90° – ∠PAB
= 90° – 65° = 25°
Question 24.
The quadratic equation x2 – 3x + p = 0 has distinct real roots, then find the value of p.
Answer:
Given quadratic equation is x2 – 3x + p = 0
On comparing with ax2 + bx + c = 0, we get
a = 1,
b = – 3
and c = p
The condition for distinct real roots is b2 – 4ac > 0
⇒ (- 3)2 – 4 (1) (p) > 0
⇒ 9 – 4p > 0
⇒ 9 > 4p
⇒ 4p < 9
⇒ p < \(\frac{9}{4}\)
![]()
Question 25.
A sphere of diameter 6 cm is dropped in a right circular cylindrical vessel partly filled with water. The diameter of the cylindrical vessel is 12 cm. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel?
Solution:
Diameter of sphere = 6 cm
Diameter of cylindrical vessel = 12 cm
Volume of sphere = \(\frac{4}{3}\) πr3
= \(\frac{4}{3}\) × M × 3 × 3 × 3
= 36m cm2
∴ Volume of sphere = Increase in volume of cylinder
36π = π(6)2 × h
h=1cm
∴Level of water rise in vessel = 1 cm
OR
The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. Find the area of the sector.
Solution:
Given, radius of circle (r) = 5.2 cm
ie., OA = OB=r=5.2cm
and the perimeter of a sector = 16.4cm
As we know that perimeter of the sector
= 2r + \(\frac{2 \pi r \theta}{360^{\circ}}\)
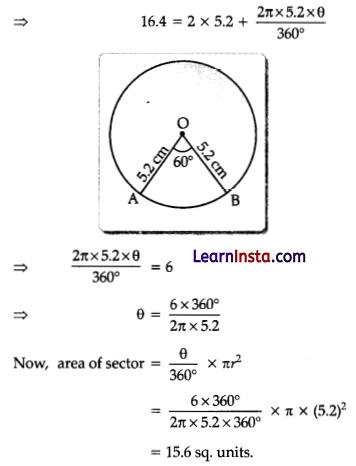
Section -C(18 Marks)
Question 26.
Three bells toll at intervals of 9, 12, and 15 minutes respectively. If they start tolling together, after what time will they next toll together?
Solution:
LCM (9, 12,15) = 2 × 2 × 3 × 3 × 5 = 180
Three bells will toll together after 180 minutes.
ie., In 3 hours they will toll next.
Question 27.
Find the zeroes of the quadratic polynomial 4s2 – 4s + 1 and verify the relationship between the zeroes and the coefficients. 3
Answer:
P(s) = 4s2 + 4s + 1
4s2 – 2s – 2s + 1 = 0
2s (2s – 1) – 1 (2s – 1) = 0

Question 28.
Represent the following pair of linear equations graphically and hence comment on the condition of consistency of this pair.
x – 5y = 6, 2x -10y = 12.
Solution:
Given, x – 5y = 6 ⇒ y = \(\frac{x-6}{5}\)
| x | 6 | 1 | -4 |
| y | 0 | -1 | -2 |
and 2x – 10y = 12 ⇒ y = \(\frac{x-6}{5}\)
| x | 6 | 1 | -4 |
| y | 0 | -1 | -2 |
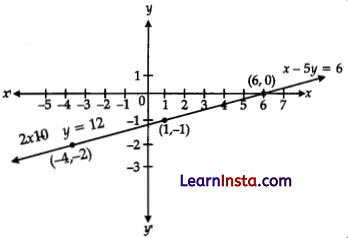
From above a system of equation has infinite many solutions. hence, A system of equation is consistent. (as we know system of equations is called consistent if there is at least one set of values for the unknowns that satisfies each equation in the system.)
OR
The sum of ages (in years) of a son and his father is 35 years and product of their ages is 150 years, find their ages.
Solution:
Let the age of father be x years.
and age of son be y years.
x + y = 35 and xy = 150
or y =35 – x
Putting the value of y in xy = 150
x(35 – x) = 150
⇒ x2 – 35x + 150 =0
⇒ (x – 30)(x – 5) =0
⇒ x = 30 or x = 5 (rejected)
y = 5
Hence; the age of father = 30 years and the age of son = 5 years.
![]()
Question 29.
Prove that the lengths of tangents drawn from an external point to a circle are equal.
Solution:
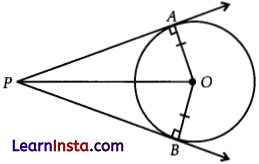
In ΔOPA and ΔOPB
∠PAO = ∠PBO (each 90°)
OP = PO (common)
OA = OB (tadii of same circle)
ΔOPA = ΔOPB (by RHS congruency axiom)
Hence, PA = PB (by cpct)
Question 30.
Prove that sin θ (1 + tan θ) + cos θ (1 + cot θ) = sec θ + cosec θ
Answer:
L.H.S. = sin θ (1 + tan θ) + cos θ (1 + cot θ)

OR
If sin (A + 2B) = \(\frac{\sqrt{3}}{2}\) and cos(A + 4B) = 0, A > Band A, B ≤ 90°, then find A and B.
Solution:
We have sin (A + 2B) = \(\frac{\sqrt{3}}{2}\)
∴ sin (A + 2B) = sin 60°
⇒ A+ 2B =60° …(i)
and cos (A + 4B) = 0
∴ cos (A+ 4B) = cos 90° [∴ cos 90° = 0]
⇒ (A+ 4B) = 90° …(ii)
Solving eq. (i) and (ii), we get
A = 30° and B = 15°.
Question 31.
An integer is chosen between 70 and 100. Find the probability that it is.
(i) a prime number
(ii) divisible by 7.
Solution:
Total number of integers in between 70 and 100 = 29
(i) Numbers that are prime is between 70 and 100 are {71, 73, 79, 83, 89, 97}
Probability (prime number) = \(\frac{6}{29}\)
(ii) Numbers that are divisible by 7 in between 70 and 100 are {77, 84, 91, 98}
Probability (number divisible by 7) = \(\frac{6}{29}\)
Section – D(20 Marks)
Question 32.
The first term of an AP is 3, the last term is 83 and the sum of all its terms is 903. Find the number of terms and the common difference of the A.P.
Solution:

OR
The sum of four consecutive numbers in A.P is 32 and the ratio of the product of the first and last term to the product of two middle terms is 7: 15, Find the numbers.
Solution:
Let the four consecutive terms of A.P. be
(a – 3d), (a – d), (a + d) and (a + 3d).
By given conditions
a – 3d + a – d + d + a + 3d = 32
⇒ 4a = 32
⇒ a = 8
and \(\frac{(a-3 d)(a+3 d)}{(a-d)(a+d)}=\frac{7}{15}\)
\(\frac{a^2-9 d^2}{a^2-d^2}=\frac{7}{15}\)
(On putting value of a = 8 from above)
d2 = 4
d = ± 2
Hence, the numbers are 2, 6, 10 and 14 or 14, 10, 6 and 2.
Question 33.
Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
In ΔPQR, S and T are points on PQ and PR respectively. \(\) and ∠PST = ∠PRQ.
Prove that PQR is an isosceles triangle. 5
Answer:
Given, in ΔABC, DE || BC
To prove \(\frac{A D}{D B}=\frac{A E}{E C}\)
Construction: join BE and CD
Draw DM ⊥ AC and EN ⊥ AB

Proof:
Area of ΔADE = \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × AD × EN ………… (i)
Area (ΔDBE) = \(\frac{1}{2}\) × DB × EN ……… (ii)
Divide eqn (i) by (ii)

area ΔADE = \(\frac{1}{2}\) × AE × DM …………. (iv)
area ΔDEC = \(\frac{1}{2}\) × EC × DM ……….. (v)
Divide eqn (iv) by (v)

ΔBDE and ΔDEC are on the same base DE and between same parallel lines BC and DE
∴ area (ΔDBE) = area (DEC)
Hence,
![]()
[LHS or (iii) = RHS of (vi)]
\(\frac{A D}{D B}=\frac{A E}{E C}\)
[RHS of (iii) RHS of (vi)]
Since \(\frac{P S}{S Q}=\frac{P T}{T R}\)
∴ ST || QR [by converse of BPT]
∠PST = ∠PQR [Corresponding ongles] [given]
But ∠PST = ∠PRQ
∠PQR= ∠PRQ

PR = PQ
[sides opposite to equal angles are equal]
Hence, ΔPQR is isosceles.
Question 34.
The median of the following data is 525. Find the values of x and y, if total frequency is 100.
| Class | Frequency |
| 0-100 | 2 |
| 100-200 | 5 |
| 200-300 | x |
| 300-400 | 12 |
| 400-500 | 17 |
| 500-600 | 20 |
| 600-700 | y |
| 700-800 | 9 |
| 800-900 | 7 |
| 900-1000 | 4 |
Solution:
| Class Interval | Frequency | Cumulative Frequency |
| 0-100 | 2 | 2 |
| 100-200 | 5 | 7 |
| 200-300 | x | 7 + x |
| 300-400 | 12 | 19 + x |
| 400-500 | 17 | 36 + x |
| 500-600 | 20 | 56 + x |
| 600-700 | y | 56 + x + y |
| 700-800 | 9 | 65 + x + y |
| 800-900 | 7 | 72 + x + y |
| 900-1000 | 4 | 76 + x + y |
| Total | N = 100 |
Also, 76 + x + y = 100
⇒ x + y = 100 – 76 = 24
Given, Median = 525, which lies between class 500 – 600.
⇒ Median class = 500 – 600
Now, Median = i + \(\frac{\frac{N}{2}-c . f}{f}\) × h
⇒ 525 = 500 + \(\left[\frac{\frac{100}{2}-(36+x)}{20}\right]\) × 100
⇒ 25 = (50 – 36 – x)5
⇒ 14 – x = 25/2 = 5
⇒ x = 14 – 5 = 9
Putting the value of x in eq. (i), we get
y = 24 – 9 = 15
Hence, x = 9 and y = 15.
![]()
Question 35.
A parkis of the shape of a circle of diameter 7 m. It is surrounded by a path of width of 0.7 m. Find the expenditure of cementing the path. If its cost is ₹ 110 per sq. m.
Solution:
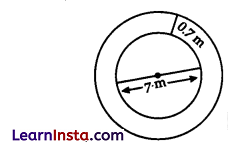
Given, the diameter of park = 7 m
Radius = \( \frac{7}{2}\) = 3.5 m
The width of path= 0.7 m
∴ Radius of park with path
= 3.5 + 0.7 = 4.2 m
Area of the path = π(4.2)2 – π(3.5)2
= \( \frac{22}{7}\)(17.64 – 12.25)
= \( \frac{7}{2}\) × 5.39 = 22 × 0.77
= 16.94 m2
Cost of the cementing the path
= 16.94 × 110
= ₹ 1863.40
OR
From a solid cylinder of height 14 cm and base diameter 7 cm, two equal conical holes each of radius 2.1 cm and height 4 cm are hollowed out. Find the volume of the remaining solid.
Solution:
Height of cylinder 14 cm
Diameter of base 7 cm
Volume of cylinder= πr2h
= \( \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × 14
= 11 × 7 × 7
= 539
Radius of cone 2.1 cm Height 4 cm
Volume of 2 such cones = 2× 1/3 πr2h
= 2 × – \(\frac{1}{3} \times \frac{22}{7}\) × 2.1 × 2.1 × 4
= 44 × 0.1 × 2.1 × 4
= 36.96
Volume of remaining solid is 539 – 36.96
= 502.04
Section – E(12 Marks)
Question 36.
Vikas is working with TCS and he is sincere and dedicated to his work. He pays all his taxes on time and invests some amount of his salary in funds for his future.

He invested some amount at the rate of 12% simple interest and some other amount at the rate of 10% simple interest. He received yearly interest of ₹ 130. But, if he interchange the amounts invested, he would have received ₹ 4 more as interest.
Based on the above information, answer the following questions.
(i) Consider the amount invested at 12% be p and at 10% be q. Then, formulate the required linear equation for first condition.
Answer:
Vikas received ₹ 130 as profit.
∴ According to the situation,
\(\frac{12}{100}\) p + \(\frac{10}{100}\) q = 130
⇒ 12p + 10q = 13000
(ii) Formulate the linear equation for the second condition?
Answer:
Vikas received ₹ 4 extra, if he interchange the investment amount,
∴ According to the situation,
\(\frac{10}{100}\) p + \(\frac{12}{100}\) q = 130 + 4
⇒ 10p + 12q = 13400
(iii) Find the value of p and q.
Answer:
From above situations, we have
12p + 10q = 13000 ………….(i)
and 10p + 12p = 13400 ……………..(ii)
On adding Eqs, (i) and (ii), we get
22p + 22q = 26400
⇒ p + q = 1200 ………….(iii)
Now, subtracting Eq. (ii) from Eq. (i), we get
2p – 2q = – 400
⇒ p – q = – 200 …………..(iv)
Now, on adding Eqs. (iii) and (iv), we get
2p = 1000
⇒ p = ₹ 500
On putting the value of p in Eq. (iii)
q = 1200 – 500 = ₹700
Or
Solve the following pair of equations
2x + y = 8
3x + y = 20
Answer:
We have, 2x + y = 8 …………(i)
3x + y = 20 ………………..(ii)
⇒ y = 20 – 3x
On substituting the value of y in Eq. (i), we get
2x + 20 – 3x = 8
⇒ – x = 8 – 20 = – 12
⇒ x = 12
On putting the value of x in Eq. (i), we get
2 × 12 + y = 8
⇒ y = 8 – 24
⇒ y = – 16
![]()
Question 37.
The diagram show the plans for a sun room. It will be built onto the wall of a house. The four walls of the sun room are square clear glass panels. The roof is made using,
Four clear glass panels, trapezium in shape, all of the same size
One tinted glass panel, half a regular octagon in shape
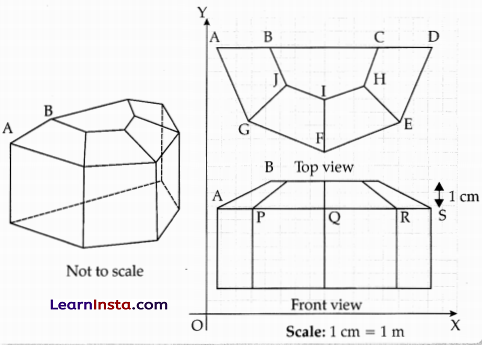
(i) Refer to Top View, find the mid-point of the segment joining the points J(6, 17) and I(9, 16).
(ii) Refer to front View, find the distance of the point P from the Y-axis.
(iii) Refer to front view, find the distance between the points A and S.
Solution:
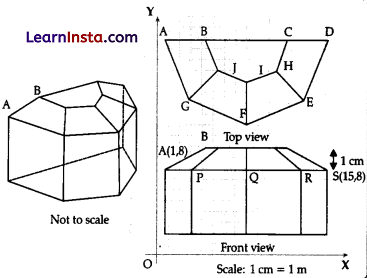
(i) Mid-point of J(6, 17) and I(9, 16) is
x = \(\frac{6+9}{2}\) and y = \(\frac{17+16}{2}\) x = \(\frac{15}{2}\) and y = \(\frac{33}{2}\)
(ii) The distance of the point P from the Y-axis = 4.
(iii) A’s coordinates = (1, 8)
S’s coordinates= (15, 8)
Then, AS \(\begin{aligned}
& =\left|\sqrt{(15-1)^2+(8-8)^2}\right| \\
& =\sqrt{(14)^2}
\end{aligned}\) = 14
OR
Refer to front view, find the co-ordinates of the point which divides the line segment joining the points A and B in the ratio 1 : 3 internally.
Solution:
The coordinates of A = (1, 8)
The coordinates of B = (4, 10)
and, m = 1 and n = 3
then, (x, y) \(\begin{aligned}
& =\left(\frac{1 \times 4+3 \times 1}{1+3}, \frac{1 \times 10+3 \times 8}{1+3}\right) \\
& =\left(\frac{7}{4}, \frac{34}{4}\right)
\end{aligned}\)
= (1.75, 8.5)
Question 38.
‘Skysails’ is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.
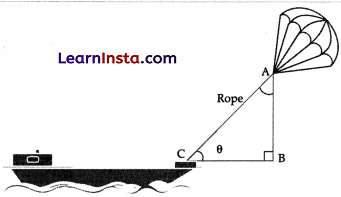
(i) In the given figure, tan θ = cot 60 where θ is acute angles, find the value of 8.
(ii) Find the value of tan 30°. cot 60°.
(iii) What should be the length of the rope of the kite sail in order to pull the ship at the angle θ and be at a vertical height of 200 m?
Solution:

OR
If cos A = \(\frac{1}{2}\); then the value of 9 cot2 A – 1.
Solution:
