CBSE Sample Papers for Class 10 Maths Basic Set 2 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths Basic with Solutions and marking scheme Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Basic Set 2 with Solutions

Maximum Marks: 80
Time Allowed: 3 hours

General Instructions:

1. This Question paper has 5 Sections A, B,C, D, and E.
2. Section B has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answers-I (SA-l) type questions carrying 2 marks each.
4. Section C has 6 Short Answers-I (SA-II) type questions carrying 3 marks each.
5. Section D has 4 Long Answers (LA) type questions carrying 5 marks each.
6. Section E has 3 source-based/case-based/passage-based integrated units of assessment (4 marks each) with sub-parts of the values of 1, 1, and 2 marks each respectively.
7. All questions are compulsory. However, an internal choice in 2 Q’s of 2 marks, 2.Q’s of 3 marks and 2 Q’s of 5 marks has been given provided. An internal choice has been provided in 2-mark questions of section E.
8. Draw neat figures wherever required. Take x = 22/7 wherever required if not stated.

Section-A(20 Marks)

Question 1.
M and N are positive integers such that M = p²q³r and N = p³q² where p, g, r are prime numbers. Find LCM (M,N).
(A) p²q³r
(B) p³q³r
(C) pqr
(D) p²q³r³
Solution:
(B) p³q³r
Explanation: M = p²q³r =p × p × q × q × q × r
and N = p³ × q² = p × p × p × q × q
Clearly, LCM (M, N) = p²q³r.

Question 2.
According to Fundamental theorem of Arithmetic, Composite number = … of prime numbers:
(A) Sum
(B) Product
(C) Difference
(D) Ratio
Solution:
(C) Suman
Explanation: According to fundamental theorem of arithmetic, we know that
Composite number = Product of primes

Question 3.
The distance between (7, 0) and (1, – 8) is: 1
(a) 7 units
(b) 10 units
(c) 8 units
(d) 9 units
Answer:
(b) 10 units
Explanation: Distance between (7, 0) and (1.-8)
[By distance formula]
= \(\sqrt{(1-7)^2+(-8-0)^2}\)
= \(\sqrt{(-6)^2+(-8)^2}\)
= \(\sqrt{36+64}\)
= \(\sqrt{100}\) = 10 units

Question 4.
If a pair of linear equations given by a₁x + b₁y + c₁ = 0 and a₂x + b²y + c₂ = 0 has a unique solution, then which of the following is true?
(A) a₁a₂ = b₁b₂
(B) a₁b₂ ≠ a₂b₁
(C) \(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)
(D) \(\frac{a_1}{b_2} \neq \frac{b_1}{a_2}\)
Solution:
(B) a₁b₂ ≠ a₂b₁
Explanation: If equations  a₁x + b₁y + c₁ = 0 and a₂x + b²y + c₂ = 0 are having unique solution then \(\frac{a_1}{b_2} \neq \frac{b_1}{a_2}\)
⇒  a₁b₂ ≠ a₂b₁

Question 5.
If 2s the one root of the equation 2x² + ax + 6= 0 then a =?
(A) 7
(B) -7
(C) -7/2
(D) 7/2
Solution:
(B) -7
Explanation: 2x² + ax + 6 = 0
2 is a root of the given equation
∴ 2(2)² + a(2) +6=0
∴ 8 + 2a + 6 = 0
⇒ 2a = -14
⇒ a = -7

Question 6.
If a = 10 and d = 7, then the first four terms will be
(a) 10, 3, – 4, – 11
(b) 3, 10, 17, 24
(c) 10, 17, 24, 31
(d) 7, 17, 27, 37
Answer:
(c) 10, 17, 24, 31

(c) Given, a = 10 and d = 7
We know that,
a_n = a + (n – 1) d
∴ a₁ = 10 + (1 – 1) (7) = 10,
a₂ = 10 + (1) (7) = 17,
a₃ = 10 + (2) (7) = 24
and a₄ = 10 + (3) (7) = 31

Question  7.
Which of the following are DEFINITELY similar to each other?
(A) any two rhombuses
(B) any two right triangles
(C) any two regular pentagons
(D) any two isoceles triangles
Solution:
(C) any two regular pentagons
Explanation: Two regular pentagons are similar in shape notin size that is why they both are definitely similar to each other.

Question  8.
If triangle ABC ∼ Triangle RPQ, AB = 3 cm, BC = 5 cm, AC = 6 cm, RP = 6 cm and PQ = 10 cm, then find QR.
(A) 12
(B) 2
(C) 6
(D) 24
Solution:
(A) 12

Question 9.
The pairs of equations x + 2y – 5 = 0 and – 4x – 8y + 20 = 0 have: 1
(a) unique solution
(b) exactly two solutions
(c) infinitely many solutions
(d) no solution
Answer:
(c) infinitely many solutions
Explanation:
\(\frac{a_1}{a_2}=\frac{1}{-4}\)
\(\frac{b_1}{b_2}=\frac{2}{-8}=\frac{1}{-4}\)
\(\frac{c_1}{c_2}=\frac{-5}{20}=-\frac{1}{4}\)
This shows:
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Therefore, the pair of equations has infinitely many solutions.

Question 10.
In the triangles shown below, ∠Q = ∠T.

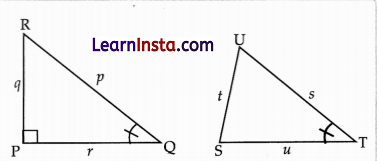
Write an expression each for cos Q and sin T.
(A) \(\frac{r}{q}, \frac{q}{p}\)
(B) \(\frac{p}{q}, \frac{q}{r}\)
(C) \(\frac{r}{p}, \frac{q}{p}\)
(D) None of these
Solution:
(C) \(\frac{r}{p}, \frac{q}{p}\)

Question 11.
The length of a string between a kite and a point on the ground is 85 m. If the string makes an angle θ with the ground level such that tan θ = 15/8, then the kite is at what height from the ground?
(A) 75 m
(B) 79.41 m
(C) 80 m
(D) 72.5 m
Solution:
(A) 75 m

Question 12.
In ∆ ABC, it is given that \(\frac{A B}{A C}=\frac{B D}{D C}\)
If ∠B = 70° and ∠C = 50°, then ∠BAD is
(a) 30°
(b) 40°
(c) 45°
(d) 50°
Answer:
(a) 30°

∠A = 180° – (70° + 50°) = 60°

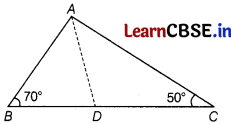
Since, \(\frac{B D}{D C}=\frac{A B}{A C}\)
[it means AD is the bisector of ∠A]
⇒ ∠BAD = \(\frac{1}{2}\) × 60° = 30°

Question 13.
In the following figure, O is the centre of the circle and PQ and PS are tangents to the circle at points Q and S respectively, find Angle QRS.

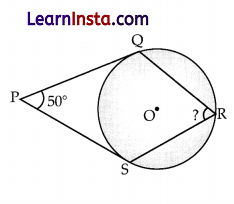
(A) 45°
(B) 55°
(C) 65°
(D) 90°
Solution:
(C) 65°

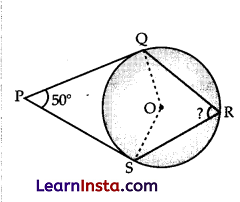
Explanation: Join OQ and OS.
As, OQ and OS are radii of the circle and radius is perpendicular to the tangent at point of contact.
Therefore, OQ ⊥ PQ and OS1 PS
⇒ ∠QOS + ∠OSP + ∠QPS + ∠OQP = 360°
⇒ ∠QOS + 50° + 90° + 90° = 360°
⇒ ∠QOS = 360° -230°
⇒ ∠QOS = 130°
According to the theorem, angle subtended by an arc at the centre of the circle is double the angle subtended it at any point on the circle.
Therefore, ⇒ QOS ⇒ 2∠QRS
⇒ QRS = ∠QOS/2 = 130/2 = 60°

Question 14.
The area of a quadrant of a circle where the circumference of circle is 176 m, is
(A) 2464 m²
(B) 1232 m²
(C) 616 m²
(D) 308 m²
Solution:
(C) 616 m²

Question 15.
Two coins are tossed simultaneously. The probability of getting at least one head is: 1
(a) \(\frac{3}{4}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{2}{5}\)
(d) \(\frac{5}{4}\)
Answer:
(a) \(\frac{3}{4}\)
Explanation: Possible outcomes
= {HH, HT, TH, TT} = 4
Favourable outcomes = {HH, HT, TH} = 3
So, required probability = \(\frac{3}{4}\)

Question 16.
The heights of plants in Dipti’s garden are recorded in the table given below. The median plant height is 55 cm.

Which of the following is the value of x?
(A) 1
(B) 2
(C) 8
(D) (the value of x cannot be found without knowing the total number of plants)
Solution:
(B) 2

Height of plants	Number of plants	Cummulative frequency
0-20	2x	2x
20-40	4	2x + 4
40-60	4x	6x + 4
60-80	8	6x + 12
80-100	4	x + 16
Total	6x + 16

Question 17.
If two solid hemispheres of same base radius Y are joined together along their bases, then curved surface area of this new solid is:
(A) 4πr²
(B) 6πr²
(C) 3πr²
(D) 8πr²
Solution:
(A) 4πr²
Explanation: When two hemispheres of equal radii are joined base to base, new solid becomes sphere and curved surfrace area of sphere is 4πr².

Question 18.
If the HCF of 45 and 55 is 5, LCM of 45 and 55 is 99 x a, then the value of a is
(a) 25
(b) 49
(c) 5
(d) 7
Answer:
(c) 5

We know that,
HCF × LCM = Product of two numbers
⇒ 5 × 99 × a = 45 × 55
⇒ a = \(\frac{45 \times 55}{5 \times 99}\) = 5

Directions: In the following questions, A Statement of Assertion (A) is followed by a statement of Reason (R).
Mark the correct choice as.

Question 19.
Assertion (A): The origin is the ONLY point equidistant from (2, 3) and (-2, -3).
Reason (R): The origin is the midpoint of the line joining (2, 3) and (-2, -3).
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
(D) (A) is false but (R) is true.
Explanation: As there could be infinite poins equidistant from the points (2, 3) and (-2, -3).
Also origin is a midpoint of the line segment joining the points (2, 3) and (-2, -3).
Therefore, (A) is false but (R) is true.

Question 20.
Assertion (A): If HCF of 510 and 92 is 2, then the LCM of 510 and 92 is 32460.
Reason (R): As HCF (a, b) × LCM (a, b) = a × b.
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
(D) (A) is false but (R) is true.
Explanation: As, 510 = 2 × 3 × 5 × 17 and 92 = 2 × 2 × 23.
LCM (92, 510) = 2 × 2 × 3 × 5 × 17 × 23 = 23460.

Section – B(10 Marks)

Question 21.
Write the prime factorization of 8190.
OR
Find the HCF of (2³ × 3² × 5¹), (2² × 3³ × 5²) and (2⁴ × 3¹ × 5² × 7). 2
Answer:
The prime factorization of 8190 is:
8190 = 2 × 3 × 3 × 5 × 7 × 13.

OR
The given factors are (2³ × 3² × 5¹), (2² × 3³ × 5²) and (2⁴ × 3¹ × 5² × 7)
Now, HCF = Product of each prime factors with smallest power.
HCF = 2² × 3¹ × 5¹ /.e. 60.

Question 22.
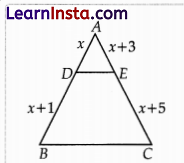
In AABC, DE || BC, find the value of x.

PQ is a tangent drawn from an external point P to a circle with centre O and QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
Solution:

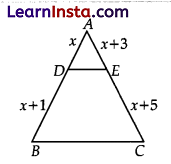
According to the basic proportionality theorem,
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct two points, the other two sides are divided in the same ratio.
As, DE || BC,
Therefore, \(\frac{A D}{D B}=\frac{A E}{E C}\)
⇒ \(\frac{x}{x+1}=\frac{x+3}{x+5}\)
⇒ x(x + 5) = (x + 3)(x + 1)
⇒ x² + 5x = x² + 3x + 1x +3
⇒ 5x- 4x = 3
⇒ x = 3

OR

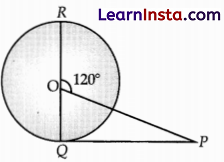
Solution:

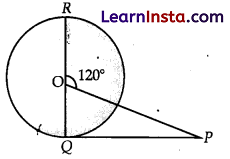
As RQ is a line.
Therefore, ∠ROQ = 180°
Or, ∠ROP + ∠POQ = 180°
Or, ∠POQ- 180° – ∠POQ
= 180° -120° = 60°
∠OQP = 90°
[Radius is perpendicular to the tangent at point of contact]
In ΔPOQ, ∠OQP + ∠POQ + ∠OPQ = 180°
Or, ∠OPQ = 180°- ∠OQP – ∠POQ
= 180° – 90° – 60°
= 30°

Question 23.
Shown below is a circle with 3 tangents KQ. KP and LM, QL = 2 cm and KL = 6 cm, PM = 1/2 KL.

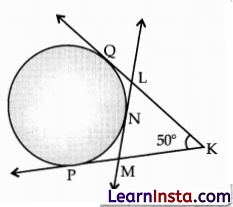
Solution:

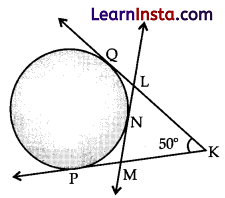
As KL = 6 cm
So, PM = 1/2 KL = 1/2 × 6 = 3 cm
KQ = KL + LQ = 6 + 2 = 8 cm And KQ = KP = 8 cm [Tangents drawn from an external point are equal in length]
MK = KP – PM = 8 – 3 = 5cm
Also, PM = MN = 3 cm
and QL = LN = 2 cm
ML = MN + LN
= 3 + 2
= 5
and MK = ML = 5 cm
[Tangents drawn from an external point are equal in length]
Therefore, ALMK is an isosceles triangle and
∠MKL = ∠KLM = 50
By, angle sum property of a triangle,
∠LMK + ∠MKL + ∠KLM = 180°
∠LMK + 50° + 50° = 180°
Clearly, ∠LMK = 80°

Question 24.
If the mean of the following distribution is 6, then find the value of p.

Solution:
Table for the product of observation and frequency

Xi	fj	fixi
2	3	6
4	2	8
6	3	18
9	1	10
p+5	2	2p+1O
Total	N = Σfi = 11	fixi = 2p + 52

We have, N = Σf_i = 11
and Σf_ix_i = 2p + 52
∴ Mean = \(\frac{\Sigma f_i x_i}{N}\)
⇒ 6 = \(\frac{2 p+52}{11}\)
⇒ 66 = 2p + 52
⇒ 14 = 2p
∴ P = 7

Question 25.
The figure below is a part of a circle with centre O. Its area is \(\frac{1250 \pi}{9} \mathrm{~cm}^2\) and the 10 sectors are identical.

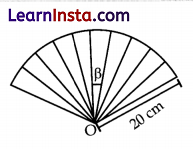
Find the value of β, in degrees. Show your steps.

Solution:

OR

The area of a circular playground is 22176 cm². Find the cost of fencing this ground at the rate of 50 per metre.
Solution:
Area of circular play ground = 22176 cm²
πr² = 22176 cm²
[where r is the radius of a play ground]
⇒ r² = 22176 × 7/22  = 7056
⇒ r = 84 cm = 0.84 m
Cost of fencing this ground = ₹ 50 × 2πr
= ₹ 50 × 2 × 22/7 × 0.84
= ₹ 264

Section – C (18 Marks)

Question 26.
Prove that 5 – √3 is irrational, given that √3 is irrational.
Solution:
Let us assume that 5 – √3 is a rational number in the form a/b
We can find co prime a & b (b≠0) such that 5 – √3 = \(\frac{a}{b}\)
Therefore, 5 – \(\frac{a}{b}\) = √3
So, we get \(\frac{5 b-a}{b}\) = √3
Since a & b are integers, we get \(\frac{5 b-a}{b}\) as rational
So, √3 is rational. But √3 is an irrational number.
Which contradicts our statement.
∴ 5 – √3 is irrational.

Question 27.
In the current scenario, the government has a policy to make a highway as soon as possible. So, the constructor used the heavy machine instead of using man labour.
A machine operator dug out a field in the shape of a circular having a radius of 3 m and a depth of 10 m.
(A) Find the volume of the soil.
(B) Find the total inner surface area of the digging field. 3
Answer:
(A) We have radius and height of cylindrical shape r = 3 m and h = 10 m.
Volume of the soil = Volume of cylinder
= πr²h
= 3.14 × (3)² × 10
= 90 × 3.14
= 282.6 m³

(B) Total inner surface area of the digging field = CSA of digging field + Area of bottom surface
= 2πrh + πr²
= 2 × 3.14 × 3 × 140 + 3.14 × (3)²
= 188.4 + 28.26
= 216.66 m²

Question 28.
Find the sum of first 16 terms of the A.E 10, 6, 2, ………..
Solution:
10,6,2,  ….. is the given A.P.
a = 10
d = 6 – 10 = -4
n = 16
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₁₆ = \(\frac{16}{2}\)[2(16) + (16 – 1)(-4)]
= 8[20 + (15)(-4)
= 8(20- 60]
= 8[-40]
= -320

OR

For what value of p will the following system of equations have no solution?
(2p – 1)x + (p – 1)y = 2p + 1; y + 3x -1 =0
Solution:

Question 29.
If a circle touches the side BC of a triangle ABC at P and extended sides AB and AC at Q and R, respectively, prove that AQ = 1/2 (BC + CA + AB)
Solution:
BC + CA+ AB
= (BP + PC) + (AR – CR) + (AQ – BQ)
= AQ + AR – BQ + BP + PC – CR

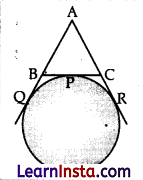
∴ From the same external point, the tangent segments drawn to a circle are equal.
From the point B, BQ = BP
From the point A, AQ = AR
From the point C, CP = CR
∴ Perimeter of ΔABC,
AB + BC + CA = 2AQ – BQ + BQ + CR – CR = 2AQ
⇒ AQ = \(\frac{1}{2}\)(BC + CA + AB)

Question 30.
In the given figure, PT and PS are tangents to a circle from a point P such that PT =4 cm and ∠TPS = 60°. Find the length of chord TS. How many line segment of same length TS can be drawn in the circle?

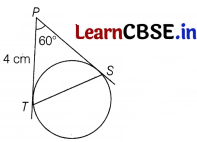
Answer:
We know that tangents drawn from external point to the circle are equal in length.
Here, P is an external point.
∴ PS = PT = 4 cm
So, ∠PTS = ∠PST
[∵ angles opposite to equal sides are equal]
In ∆PTS, we have
⇒ ∠PTS + ∠PST + ∠TPS = 180°
[by ange sum property of triangle]
⇒ ∠PTS + ∠PTS + 60° = 180°
[∵ ∠PST = ∠PTS and ∠TPS = 60°]
⇒ 2 ∠PTS = 180° – 60°
⇒ 2 ∠PTS = 120°
⇒ ∠PTS = \(\frac{120^{\circ}}{2}\) = 60°
∴ ∆PTS is an equilateral triangle.
Hence, TS = 4rm
Here, infinite lines of same length TS can be drawn in a circle.

Or

AB is a diameter and AC is a chord of a circle such that ∠BAC = 30°. If the tangent at C intersects AB produced in D, then prove that BC = BD.
Answer:
Given :AB is a diameter of the circle with centre 0
and DC is the tangent of circle and ∠BAC = 30°.
To prove : BC = BD
Construction : Join 0 to C.

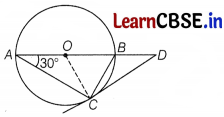
Proof : Since, OC ⊥ CD
[∵ the tangent at any point of a circle is perpendicular to the radius through the point of contact]
∴ ∠OCB + ∠BCD = 90°
Now, OC = QA [radii]
⇒ ∠OCA = ∠OAC
[angles opposite to equal sides are equal]
∴ ∠OCA = 30°
Now, ∠ACB = 90° [anglIe in a semi-circle]
∴ ∠OCA + ∠OCB = 90°
⇒ ∠OCB = 60°
and ∠BCD = 30°
In ∆ACD,
∠ACD + ∠CAD + ∠AOC = 180°
⇒ 120° + 30° + ∠ADC =180°
⇒ ∠ADC = 30°
∴ In ∆ACD,
∠BCD = ∠BDC = 30°
∴ BC = BD
Hence proved.

Question 31.
Two dice are thrown at the same time. What is the probability that the sum of the two numbers appearing on the top of the dice is:
(i) 8?
(ii) 13?
(iii) less than or equal to 12?
Solution:
The outcomes when two dices are thrown together
(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3,1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4,1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
(i) P(sum of 8) = \(\frac{\text { Favourable outcomes }}{\text { Total outcomes }}=\frac{5}{36}\)
(ii) P(sum of 13) = 0
(iii) P(less than or equal to 12) = 1

Section – D (20 Marks)

Question 32.
Solve graphically the pair of linear equations :
3x – 4y + 3 = 0 and 3x + 4y – 21 = 0.
Find the co-ordinates of the vertices of the triangular region formed by these lines and x-axis.
Solution:
Given, 3x – 4y + 3 = 0

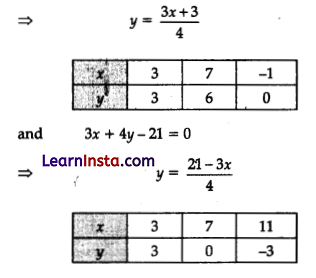
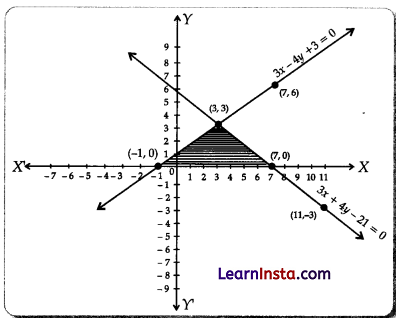
(i) These lines intersect each other at point (3, 3). Hence, x = 3 and y = 3.
(ii) The vertices of triangular region are P(3, 3), Q(-1, 0) and R(7, 0)

OR

Solve for x: \(\left(\frac{2 x}{x-5}\right)^2+5\left(\frac{2 x}{x-5}\right)\) – 24 = 0, x ≠ 5.
Solution:

Question 33.
Rahul got a total of 28 marks in math and science on a class quiz. The product of his scores would have been 180 if he had received 3 more in mathematics and 4 less in science. Find out what he scored in the two subjects.
OR
In a flight of 2800 km, an aircraft was slowed down due to bad weather, Its average speed is reduced by 100 km/h and time increased by 30 minutes, Find the original duration of the flight. 5
Answer:
Let Rahul have obtained ‘x’ marks in mathematics and ‘y’ marks in science.
Then by the problem,
x + y = 28 ……. (i)
If Rahul had got 3 marks more in mathematics, then Rahul would have got (x + 3) in mathematics and if Rahul would have got 4 marks less in science then Rahul would have got (y – 4) marks in science.
A.T.Q.
(x + 3) (y – 4) = 180
(x + 3) (28 – x – 4) = 180
⇒ (x + 3) (24 – x) = 180
⇒ 72 + 21x – x² = 180
⇒ x² – 21x + 108 = 0
⇒ x² – 12x – 9x + 108 = 0
⇒ x(x – 12) – 9(x – 12) = 0
⇒ (x – 12) (x – 9) = 0
⇒ x = 12, 9
Then, y = 16, 19
Hence, Rahul obtained 12 marks in mathematics and 16 marks in science.
Rahul obtained 9 marks in mathematics and 19 marks in science.
OR
Let the original speed of the plane be x km/hr.
∴ Reduce speed of the plane = (x – 100) km/hr.
Time taken by plane to reach its destination at original speed = \(\frac{2800}{x}\) hr
Time taken by the plane to reach its destination at reduced speed \(\frac{2800}{x-100}\) hr
∴ According to question, \(\frac{2800}{x-100}-\frac{2800}{x}\) = \(\frac{1}{2}\)
⇒ \(\frac{2800 x-2800(x-100)}{x(x-100)}\) = \(\frac{1}{2}\)
⇒ 2800 × 100 × 2 = x² – 100x
⇒ x² – 100x – 560000 = 0
⇒ x² – 800x + 700x – 560000 = 0
⇒ (x – 800) (x + 700) = 0
⇒ x = 800
or x = -700
∴ x = 800
[∵ Speed cannot be negative]
Original speed of flight = 800 km/hr
∴ Original duration of flight
= \(\frac{2800}{800}\)
= \(\frac{7}{2}\)
= 3\(\frac{1}{2}\) hrs

Question 34.
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/hour. How much area will it irrigate in 30 minutes; if 8 cm standing water is needed?
Solution:
Length of canal covered in 30 min = 5000 m
Volume of water flown in 30 min = 6 × 1.5 × 5000 m³
If 8 cm standing water is needed that area irrigated
\(=\frac{6 \times 1.5 \times 5000}{0.08}\)
= 562500 m²

OR

A vessel full of water is in the form of an inverted cone of height 8 cm and the radius of its top, which is open, is 5 cm 100 spherical lead balls are dropped into the vessel. One-fourth of the water flows out of the vessel. Find the radius of a spherical ball.
Solution:

Question 35.
Find the mode of the following distribution of marks obained by the students in an examination:

Given the mean of the above distribution is 53, using empirical relationship estimate the value of its median.
Solution:

Empirical relationship,
Mode = 3 median- 2 mean
Mode = 68 and mean = 53 (given)
3 median = mode + 2 mean
3 median = 68 + 2 × 53
Median = \(\frac{174}{3}\) = 58
Hence, Median = 58

Section -E (12 Marks)

Question 36.
To conduct Sports Day activities in your rectangular-shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each, and 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in the figure.

Niharika runs \(\frac{1}{4}\)th the distance AD on the 2nd line and posts a green flag. Preet runs \(\frac{1}{5}\)th the distance AD on the 8th line and posts a red flag.

Based on above information, answer the following questions.

(i) Write the coordinates of green flag.
Answer:
From the given figure, the position of green flag posted by Niharika is M (2 × 1, \(\frac{1}{4}\) × 100 i.e. M(2, 25),

(ii) Find the distance between both the flags.
Answer:
∵ M = (2, 25)
and N = (8, 20)
Now, MN = \(\sqrt{(8-2)^2+(20-25)^2}\)
[∵ distance = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)]
= \(\sqrt{(6)^2+(-5)^2}\)
= \(\sqrt{36+25}=\sqrt{61}\)
Hence, the distance between flags is \(\sqrt{61}\) m.

(iii) Write the coordinates of red flag.
Answer:
From the given figure, the position of red flag posted by Preet is N (8 × 1, \(\frac{1}{5}\) × 100) i.e, N (8, 20),

Or

If Rashmi has to post a blue flag exactly half way between the line segment joining the flags, then find the coordinates of that point. (2)
Answer:
Let P be the position of the blue flag posted by Rashmi in the half way of line segment MN.
Then coordinates of P = \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)
= \(\left(\frac{2+8}{2}, \frac{25+20}{2}\right)\)
= \(\left(\frac{10}{2}, \frac{45}{2}\right)\)
= (5, 22.5)
Hence, the blue flag is on the 5th line at a distance of 22.5 m above it.

Question 37.
Read the following text and answer the below questions:
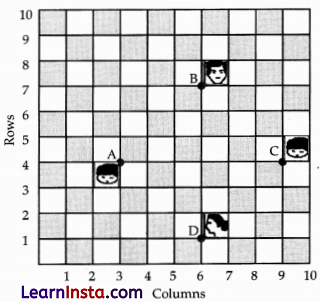
In a room, 4 friends are seated at the points A, B, C and Das shown in figure. Reeta and Meeta walk into the room and after observing for a few minutes, Reeta asks Meeta.

(i) What is the position of A and D?
(ii) What is the distance between A and B?
Solution:
(i) Point A lies in x = 3 and y = 4.
∴ A (3, 4) is the correct position.
Point D lies at x = 6 and y = 1.
So, the correct position of D is (6, 1).
(ii) Position of A = (3, 4)
Position of B = (6, 7)
∴ Distance of AB = \(\begin{aligned}
& =\left|\sqrt{(3-6)^2+(4-7)^2}\right| \\
& =\left|\sqrt{(-3)^2+(-3)^2}\right|
\end{aligned}\)
= √18 = 3√2 unit.

OR

What is the middle position of B and C?
(iii) What figure is formed when points A, B, C and D are joined? Give reason.
Solution:
Position of B = (6, 7) and position of C = (9, 4)
∴ Mid-point of B and C = \(\begin{aligned}
& =\left(\frac{6+9}{2}, \frac{7+4}{2}\right) \\
& =\left(\frac{15}{2}, \frac{11}{2}\right)
\end{aligned}\)
(iii) Coordinates of A(3, 4)
Coordinates of B(6, 7)
Coordinates of C(9, 4)
Coordinates of D(6, 1)
According to the distance formula


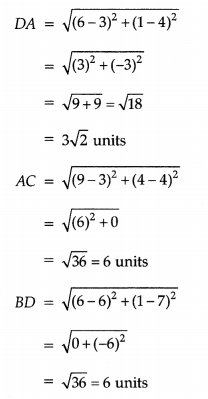
Clearly, all sides are equal and diagonals are equal.
Therefore, ABCD is a square.

Question 38.
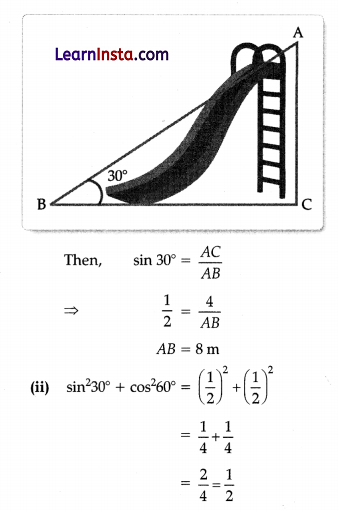
Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground the inclined at an angle of 30° to the ground.

(i) Find the distance of AB.
(ii) Find the value of sin2 30° + cos2 60°.
(iii) If sin A = \(\frac{\sqrt{3}}{2}\) then find the value of 12 Cot²A –  2.
Solution:
(i) We have, ∠B = 30° and AC = 4 m

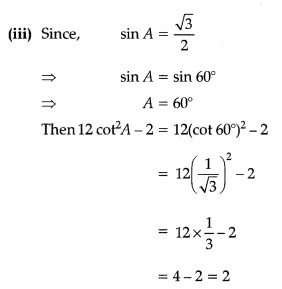
OR

In the given figure, if AB + BC = 25 and AC = 5 cm, then the value of BC.
Solution:
We have, ∠C = 90°
AB + BC = 25 cm and AC = 5 cm
Let BC be x cm, then AB = (25 – x) cm
By using Pythagoras Theorem,
AB² = BC² + AC²
⇒ (25 – x)² = x² + (5)²
⇒ 625 – 50x + x² = x² + 25
⇒ 50x  = 600
⇒ x = 600/50 = 12
Hence, BC = 12 cm