Here we are providing Number Systems Class 9 Extra Questions Maths Chapter 1 with Answers Solutions, Extra Questions for Class 9 Maths was designed by subject expert teachers.
Extra Questions for Class 9 Maths Number Systems with Answers Solutions
Extra Questions for Class 9 Maths Chapter 1 Number Systems with Solutions Answers
Number Systems Class 9 Extra Questions Very Short Answer Type
Question 1.
Simplify: (√5 + √2)2.
Solution:
Here, (√5 + √22 = (√52 + 2√5√2 + (√2)2
= 5 + 2√10 + 2 = 7 + 2√10
Question 2.
Find the value of √(3)-2.
Solution:
![]()
Question 3.
Identify a rational number among the following numbers :
2 + √2, 2√2, 0 and π
Solution:
O is a rational number.
Question 4.
Express 1.8181… in the form \(\frac{p}{q}\) where p and q are integers and q ≠ 0.
Solution:
Let x =1.8181… …(i)
100x = 181.8181… …(ii) [multiplying eqn. (i) by 100]
99x = 180 [subtracting (i) from (ii)]
x = \(\frac{180}{99}\)
Hence, 1.8181… = \(\frac{180}{99}\) = \(\frac{20}{11}\)
Question 5.
Simplify : √45 – 3√20 + 4√5
Solution:
√45 – 3√20 + 4√5 = 3√5 – 6√5 + 4√5 = √5.
Question 6.
Find the value of’
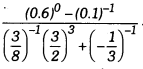
Solution:
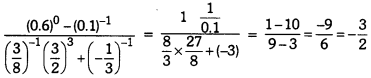
Question 7.
Find the value of
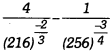
Solution:
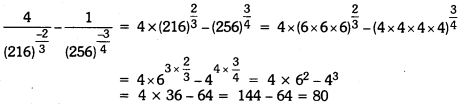
Number Systems Class 9 Extra Questions Short Answer Type 1
Question 1.
Evaluate : (√5 + √22 + (√8 – √5)2
Solution:
(√5 + √2)2 + (√8 – √52 = 5 + 2 + 2√10 + 8 + 5 – 2√40
= 20 + 2√10 – 4√10 = 20 – 2√10
Question 2.
Express \(23 . \overline{43}\) in \(\frac{p}{q}\) form, where p, q are integers and q ≠ 0.
Solution:
Let x = \(23 . \overline{43}\)
or x = 23.4343… ….(i)
100x = 2343.4343… …(ii) [Multiplying eqn. (i) by 100]
99x = 2320 [Subtracting (i) from (ii)
⇒ x = \(\frac{2320}{99}\)
Hence, \(23 . \overline{43}\) = \(\frac{2320}{99}\)
Question 3.
Let ‘a’ be a non-zero rational number and ‘b’ be an irrational number. Is ‘ab’ necessarily an irrational ? Justify your answer with example.
Solution:
Yes, ‘ab’ is necessarily an irrational.
For example, let a = 2 (a rational number) and b = √2 (an irrational number)
If possible let ab = 2√2 is a rational number.
Now, \(\frac{ab}{a}\) = \(\frac{2 \sqrt{2}}{2}\) = √2 is a rational number.
[∵ The quotient of two non-zero rational number is a rational]
But this contradicts the fact that √2 is an irrational number.
Thus, our supposition is wrong.
Hence, ab is an irrational number.
Question 4.
Let x and y be a rational and irrational numbers. Is x + y necessarily an irrational number? Give an example in support of your answer.
Solution:
Yes, x + y is necessarily an irrational number.
For example, let x = 3 (a rational number) and y = √5 (an irrational number)
If possible let x + y = 3 + √5 be a rational number.
Consider \(\frac{p}{q}\) = 3 + √5, where p, q ∈ Z and q ≠ 0.
Squaring both sides, we have
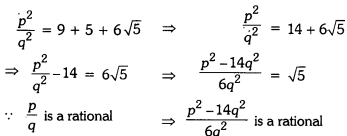
∵ \(\frac{p}{q}\) is a rational
⇒ √5 is a rational
But this contradicts the fact that √5 is an irrational number.
Thus, our supposition is wrong.
Hence, x + y is an irrational number.
Number Systems Class 9 Extra Questions Short Answer Type 2
Question 1.
Represent √3 on the number line.
Solution:
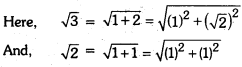
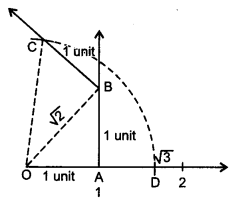
On the number line, take OA = 1 unit. Draw AB = 1 unit perpendicular to OA. Join OB.
Again, on OB, draw BC = 1 unit perpendicular to OB. Join OC.
By Pythagoras Theorem, we obtain OC = √3. Using
compasses, with centre O and radius OC, draw an arc, which intersects the number line at point
D. Thus, OD = √3 and D corresponds to √3.
Question 2.
Represent √3.2 on the number line.
Solution:
First of all draw a line of length 3.2 units such that AB = 3.2 units. Now, from point B, mark a distance of 1 unit. Let this point be ‘C’. Let ‘O’ be the mid-point of the distance AC. Now, draw a semicircle with centre ‘O’ and radius OC. Let us draw a line perpendicular to AC passing through the point ‘B’ and intersecting the semicircle at point ‘D’.
∴ The distance BD = √3.2
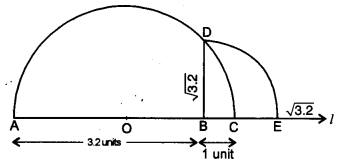
Now, to represent √3.2 on the number line. Let us take the line BC as number line and point ‘B’ as zero, point ‘C’ as ‘1’ and so on. Draw an arc with centre B and radius BD, which intersects the number line at point ‘E’.
Then, the point ‘E’ represents √3.2.
Question 3.
Express 1.32 + 0.35 as a fraction in the simplest form.
Solution:
Let . x = 1.32 = 1.3222…..(i)
Multiplying eq. (i) by 10, we have
10x = 13.222…
Again, multiplying eq. (i) by 100, we have
100x = 132.222… …(iii)
Subtracting eq. (ii) from (iii), we have
100x – 10x = (132.222…) – (13.222…)
90x = 119
⇒ x = \(\frac{119}{90}\)
Again, y = 0.35 = 0.353535……
Multiply (iv) by 100, we have …(iv)
100y = 35.353535… (v)
Subtracting (iv) from (u), we have
100y – y = (35.353535…) – (0.353535…)
99y = 35
y = \(\frac{35}{99}\)
![]()
Question 4.
Find the square root of 10 + √24 + √60 + √40.
Solution:
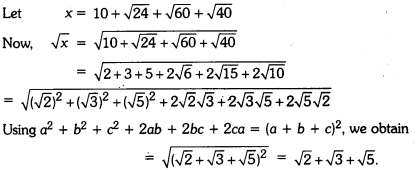
Question 5.
If x = 9 + 4√5, find the value of √x – \(\frac{1}{\sqrt{x}}\).
Solution:
Here,
x = 9 + 4√5
x = 5 + 4 + 2 x 2√5
x = (√52 + (22 + 2 x 2x √5).
x = (√5 + 2)2
√x = √5 + 2
Now, \(\frac{1}{\sqrt{x}}\) = \(\frac{1}{\sqrt{5}+2}\)
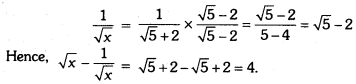
Question 6.
If x = \(\frac{1}{\sqrt{5}-2}\) , find the value of x3 – 32 – 5x + 3
Solution:
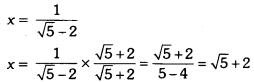
∴ x – 2 = √5
Squaring both sides, we have
x2 – 4x + 4 = 5
x2 – 4x – 1 = 0 …(i)
Now, x3 – 32 – 5x + 3 = (x2 – 4x – 1) (x + 1) + 4
= 0 (x + 1) + 4 = 4 [using (i)]
Question 7.
Find ‘x’, if 2x-7 × 5x-4 = 1250.
Solution:
We have 2x-7 × 5x-4 = 1250
⇒ 2x-7 × 5x-4 = 2 5 × 5 × 5 × 5
⇒ 2x-7 × 5x-4 = 21 × 54
Equating the powers of 2 and 5 from both sides, we have
⇒ x – 7 = 1 and x – 4 = 4
⇒ x = 8 and x = 8
Hence, x = 8 is the required value.
Question 8.
Evaluate:
![]()
Solution:
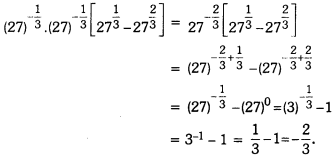
Number Systems Class 9 Extra Questions Long Answer Type
`Question 1.
If x = \(\frac { \sqrt { p+q } +\sqrt { p-q } }{ \sqrt{p+q}-\sqrt{p-q} }\), then prove that q2 – 2px + 9 = 0.
Solution:
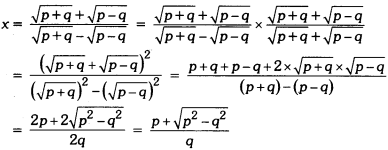
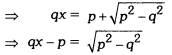
Squaring both sides, we have
⇒ q2x2 + p2 – 2pqx = p2 – q2
⇒ q2x2 – 2pqx + q2 = 0
⇒ q(q2 – 2px + q) = 0
⇒ qx2 – 2px + q = 0 (∵ q ≠ 0)
Question 2.
If a = \(\frac{1}{3-\sqrt{11}}\) and b = \(\frac{1}{a}\), then find a2 – b2
Solution:
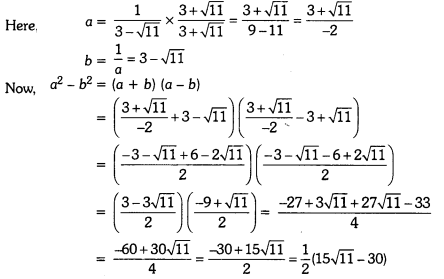
Question 3.
Simplify:
![]()
Solution:

Question 4.
Prove that:
![]()
Solution:
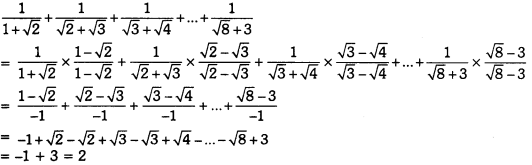
Question 5.
Find a and b, if
![]()
Solution:
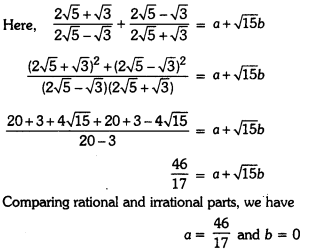
Number Systems Class 9 Extra Questions HOTS
Question 1.
If xa = y, yb = z and zc = x, then prove that abc = 1.
Solution:
We have xa = y, yb = z and zc = x
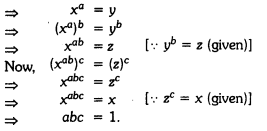
Question 2.
Prove that:
![]()
Solution:
Taking L.H.S., we have
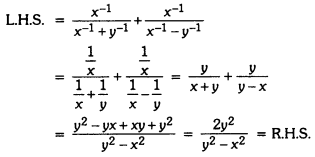
Question 3.
Show that:
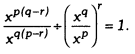
Solution:
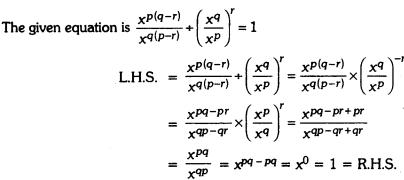
Number Systems Class 9 Extra Questions Value Based (VBQs)
Question 1.
Sudhir and Ashok participated in a long jump competition along a straight line marked as a number line. Both start the jumps one by one but in opposite directions. From ‘O’ Ashok jumps one unit towards the positive side while Sudhir jumps double in units as Ashok jumps, along negative side. After jumping 4 jumps each, at which point Ashok and Sudhir reached. What is the distance between their final positions ? Ashok argue that he is the winner since Sudhir is at negative side. Who do you think is winner and why? What is the value of the competition ?
![]()
Solution:
After jumping four jumps each, Ashok reached at 4 in positive direction and Sudhir reached at -8 i.e., in negative direction. Distance between their final positions is 12 units. Here, distance covered by Sudhir is 8 units and distance covered by Ashok is 4 units. Thus, Sudhir is the winner. Competition inculcate spirit of performance.
Question 2.
Manu went to his mathematics teacher and asked him “Sir, I want some chocolates to distribute among my classmates for my birthday but I have no money. Can you provide me some chocolates”. Teacher told Manu, I am giving you two numbers \(\frac{1}{3+2 \sqrt{2}}\) and \(\frac{1}{3-2 \sqrt{2}}\) and if you can find the value of sum of their squares, then I will provide you as many chocolates as the resulting value of sum of squares of given numbers. Find the number of chocolates. What value is depicted from this action?
Solution:
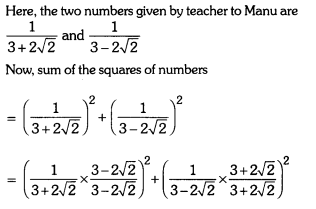
= (3 – 2√2)2 + (3 + 2√22
= 9 + 8 – 2 × 3 × (2√2) + 9 + 8 + 2 × 3 × 2√2 = 34.
Hence, resulting value of sum of squares of numbers = number of chocolates = 34. By doing this, teacher motivates the students to use their knowledge and apply it in day to day life with caring and kindness.