ML Aggarwal Class 8 Solutions for ICSE Maths Model Question Paper 3
Questions 1 to 8 is of 1 mark each.
Question 1.
Product of rational number \(\frac{-4}{7}\) and itsadditive inverse is
(a) \(\frac{16}{49}\)
(b) \(\frac{-16}{49}\)
(c) 1
(d) 0
Solution:

Question 2.
What should be subtracted from \(\frac{-3}{5}\) to get \(\frac{-2}{3}\)?
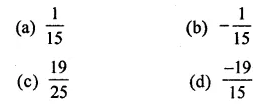
Solution:
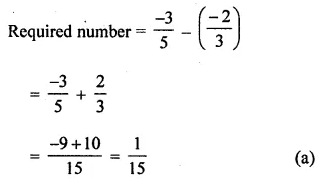
Question 3.
The value of \(\left(\frac{2}{3}\right)^{0}+\left(\frac{2}{3}\right)^{-1}\) is

Solution:
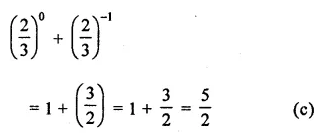
Question 4.
Standard form of 0.00000000234 is
(a) 2.34 × 10-8
(b) 23.4 × 10-10
(c) 2.34 × 10-9
(d) 234 × 10-1
Solution:
![]()
Question 5.
The volume of a cube is 216 m3. Length of its side is
(a) 3 m
(b) 6 m
(c) 9 m
(d) 12 m
Solution:
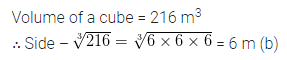
Question 6.
When the difference of a 2-digit number ab (a > b) and the number obtained by reversing the digits is divided by 9, then quotient is
(a) a + b
(b) b – a
(c) a – b
(d) none of these
Solution:

Question 7.
Amar buys a toy for ₹ 120 and sells it for ₹ 144, his profit % is
(a) 5%
(b) 10%
(c) 20%
(d) 24%
Solution:

Question 8.
If 567×8 is divisible by 9, then value of x is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
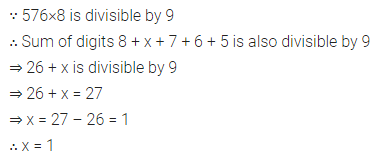
Section-B
Questions 9 to 14 are of 2 marks each.
Question 9.
Ramesh bought a fan for ₹ 1320 including 10% VAT. Find the price of the fan before VAT was added.
Solution:
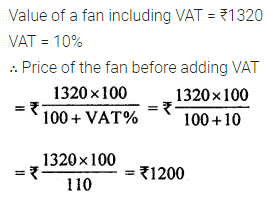
Question 10.
Find A in the addition
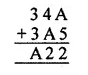
Solution:
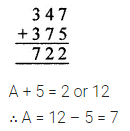
Question 11.
Find the value of x for which \(\left(-\frac{4}{5}\right)^{2} \times\) \(\left(-\frac{5}{4}\right)^{2 x}=\frac{625}{256}\).
Solution:
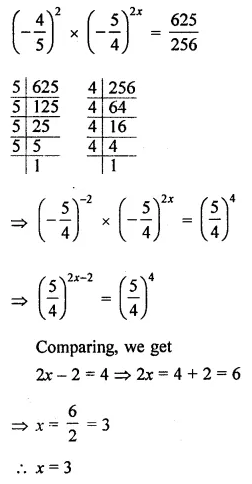
Question 12.
Using appropriate properties of operations of rational numbers, evaluate:
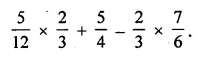
Solution:
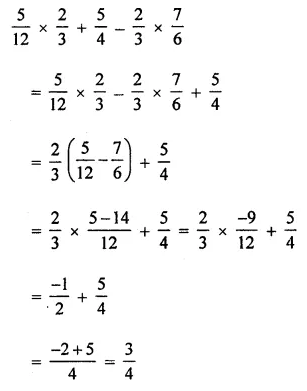
Question 13.
What number should be subtracted from the sum of \(\frac{-5}{12}\) and \(\frac{2}{3}\) to get \(\frac{5}{4}\) ?
Solution:
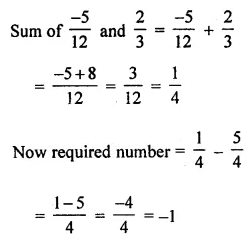
Question 14.
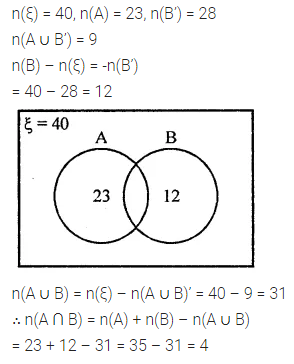
If n(ξ) = 40, n(A) = 23, n(B’) = 28 and n(A ∪ B’) = 9, find n(A ∩ B).
Solution:
Section-C
Questions 15 to 24 are of 4 marks each.
Question 15.
In an auditorium, the number of rows is equal to the number of chairs in each row. If there are 5184 chairs in the auditorium, find the number of rows.
Solution:
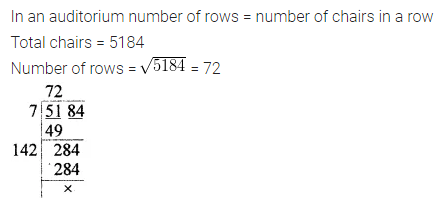
Question 16.
Insert 5 rational numbers between \(\frac{1}{3}\) and \(\frac{1}{2}\).
Solution:
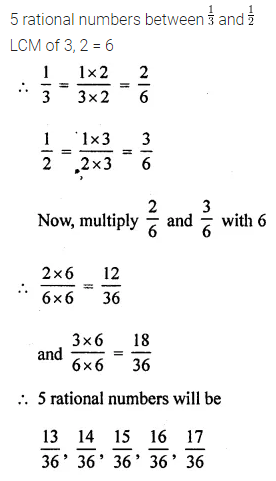
Question 17.
Find the smallest number by which 10584 should be multiplied so that product is a perfect cube. Also find the cube root of the product.
Solution:

Question 18.
In a 3-digit number unit’s digit is 2 less than hundred’s digit and hundred’s digit is 3 less than the ten’s digit. If the sum of the original number and number obtained by reversing the digits is 968, find the number.
Solution:

Question 19.
Rohit purchased some oranges at 3 for ₹5 and sold them at 5 for ₹12. Thus he gained ₹143 in all. How many oranges did he purchase?
Solution:

Question 20.
How much per cent above the cost price should a shopkeeper mark his goods so that after allowing a discount of 20% he still earns a profit of 20%?
Solution:

Question 21.
Find the difference between S.I. and C.I. on ₹2000 for \(1 \frac{1}{2}\) years at 6% p.a., compound interest being reckoned half-yearly.
Solution:


Question 22.
If 5 men or 7 women can earn ₹903 in a day, how much will 10 men and 5 women earn in a day?
Solution:
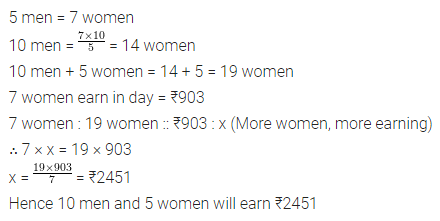
Question 23.
A hostel had rations for 150 students for 60 days. After 12 days, 30 more students join the hostel. How long will the remaining rations last?
Solution:

Question 24.
Simplify the following expression and write in the exponential form:
3-5 × 32 ÷ 36 × (22 × 3)2 + \(\left(\frac{2}{3}\right)^{-1}\) + 2-1 + \(\left(\frac{1}{19}\right)^{-1}\).
Solution:
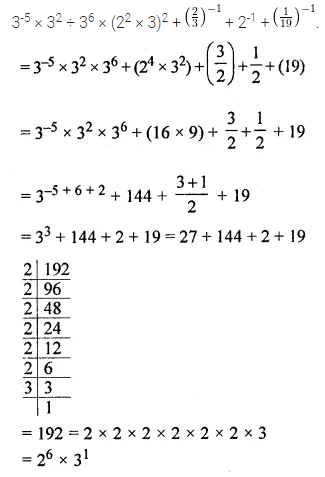
Section-D
Questions 25 to 29 are of 6 marks each.
Question 25.
Ramesh scored 30% marks in an exam and failed by 20 marks, while Suresh scored 40% marks and got 40 marks more than the minimum marks required to pass the exam. Find the maximum marks and pass percentage.
Solution:
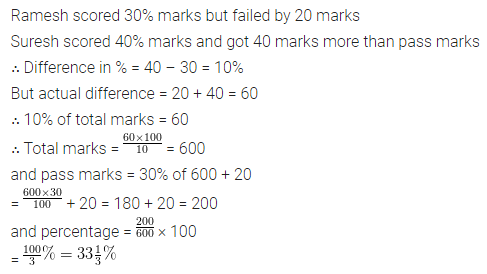
Question 26.
If ξ = {x | x ϵ W, x < 20}, A = {factors of 18} and B = {multiples of 3}, find
(i) A ∪ B
(ii) A ∩ B
(iii) (A ∪ B)’.
Also verify that n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
Solution:

Question 27.
A and B together can do a piece of work in 15 days; B and C together can do it in 12 days; C and A can do it in 20 days. How long will they take to finish the work, working together? Also find the number of days taken by each to do the same work, working alone.
Solution:


Question 28.
Is 31104 a perfect square number? If not then find the smallest number by which 31104 should be divided so that quotient is a perfect square. Also, find the square root of the quotient.
Solution:
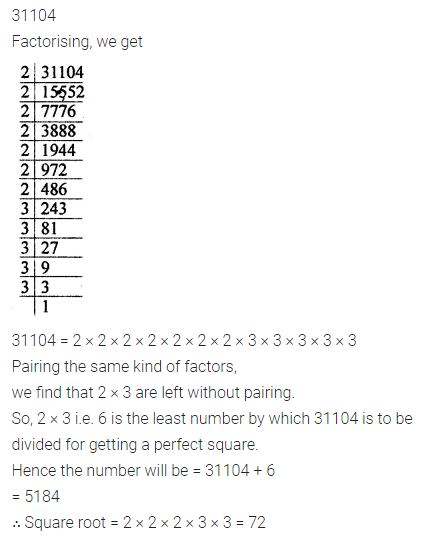
Question 29.
Three numbers are in the ratio 1:3:5 and sum of their cubes is 52479. Find the numbers.
Solution:
