Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 3 Current Electricity. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.
Class 12 Physics Chapter 3 Important Extra Questions Current Electricity
Current Electricity Important Extra Questions Very Short Answer Type
Question 1.
A wire or resistivity ρ is stretched to double its length. What will be its new resistivity?
Answer:
The resistivity remains the same as it does not depend upon the length of the wire.
Question 2.
What is the effect of temperature on the relaxation time of electrons in a metal?
Answer:
The relaxation time of electrons decreases with the rise in temperature of the metal.
Question 3.
Which physical quantity does the voltage versus current graph for a metallic conductor depict? Give its SI unit.
Answer:
It represents resistance. It is measured in ohm.
Question 4.
Define drift velocity of electrons.
Answer:
The mean velocity acquired by electrons in a conductor when an external electric field is applied to it.
Question 5.
A resistance R is connected across a cell of emf ε and internal resistance r. A potentiometer now measures the potential difference between the terminals, of the cell as V., Write the expression for ‘r’ in terms of ε, V and R. (CBSE Delhi 2011)
Answer:
The required relation is r = \(\left(\frac{\varepsilon}{V}-1\right)\)R
Question 6.
How is the drift velocity in a conductor affected by the rise in temperature? (CBSE Delhi 2019)
Answer:
It decreases.
Question 7.
Two students A and B were asked to pick a resistor of 15 kΩ from a collection of carbon resistors. A picked a resistor with bands of colours brown, green, orange, while B chose a resistor with bands of black, green, red. Who picked the correct resistor? (CBSE AI 2013C)
Answer:
A
Question 8.
Define the term ‘Mobility’ of charge carriers in a conductor. Write its S.l. unit. (CBSE Delhi 2014, AI 2015)
Answer:
Mobility of charge carriers in a conductor is defined as the magnitude of their drift velocity per unit applied electric field. Its SI unit is m2 V-1 s-1.
Question 9.
How does the mobility of electrons in a conductor change, if the potential difference applied across the conductor is doubled, keeping the length and temperature of the conductor constant? (CBSE Delhi 2019)
Answer:
No change.
Question 10.
Graph showing the variation of current versus voltage for a material GaAs is shown in the figure. Identify the region of
(i) negative resistance (ii) where Ohm’s
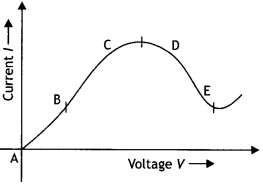
Answer:
(i) DE (ii) AB
Question 11.
Define mobility of a charge carrier. What is its relation with relaxation time? (CBSEAI 2016)
Answer:
It is defined as the drift velocity per unit electric field. The relation is μ = \(\frac{-e \tau}{m}\).
Question 12.
Nichrome and copper wires of the same length and same radius are connected in series. Current l is passed through them. Which wire gets heated up more? Justify your answer. (CBSEAI 2017)
Answer:
Nichrome, as it has more resistivity.
Question 13.
When a potential difference is applied across the ends of a conductor, how is the drift velocity of the electrons related to the relaxation time? (CBSE Delhi 2019)
Answer:
Drift velocity is directly proportional to the relaxation time.
Vd = \(\frac{e E}{m} \tau\)
Question 14.
Two bulbs are marked 60 W, 220 V and 100 W, 220 V. These are connected in parallel to 220 V mains. Which one out of the two will glow brighter?
Answer:
In parallel combination, the bulb having, more power glows more. Therefore the bulb marked 100 W, 220 V glows brighter.
Question 15.
A heater joined in parallel with a 60 W bulb is connected to the mains. If the 60 W bulb is replaced by a 100 W bulb, will the rate of heat produced by the heater be more, less or remain the same?
Answer:
The rate of heat produced in the heater will be the same as the two are connected in parallel.
Question 16.
Two conductors, one having resistance R and another 2R, are connected in turn across a dc source. If the rate of heat produced in the two conductors is Q1 and Q2 respectively, what is the value of Q1/ Q2?
Answer:
We know that Q = \(\frac{V^{2}}{R}\)t, therefore
\(\frac{Q_{1}}{Q_{2}}=\frac{R_{2}}{R_{1}}=\frac{2 R}{R}\) = 2
Question 17.
When electrons drift in metal from lower to higher potential, does it mean that all the free electrons of the metal are moving in the same direction? (CBSE Delhi 2012)
Answer:
No.
Question 18.
How does one explain the increase in resistivity of metal with an increase in temperature? (CBSE AI 2014C)
Answer:
With the increase in temperature, the average relaxation time decreases; this causes an increase in resistivity.
Question 19.
A carbon resistor is marked in red, yellow and orange bands. What is the approximate resistance of the resistor?
Answer:
24 × 103 ohm ± 20%
Question 20.
If potential difference V applied across a conductor is increased to 2 V, how will the drift velocity of the electrons change?
Answer:
The drift velocity is given by the expression Vd = \(\frac{e V}{m L}\)τ Therefore if the potential is doubled, drift velocity is also doubled.
Question 21.
What is the largest voltage you can safely put across a resistor marked 98 ohm – 0.5 W?
Answer:
Using the expression
V = \(\sqrt{P R}=\sqrt{0.5 \times 98}\) = 7 V
Question 22.
Two wires A and B are of the same metal, have the same area of cross-section and have their lengths in the ratio 2:1. What will be the ratio of currents flowing through them respectively, when the same potential difference is applied across the length of each of them?
Answer:
\(\frac{I_{\mathrm{A}}}{I_{\mathrm{B}}}=\frac{R_{\mathrm{B}}}{R_{\mathrm{A}}}=\frac{l_{\mathrm{A}}}{l_{\mathrm{B}}}=\frac{2}{1}\)
Question 23.
How does the heat produce in a resistor depend on its resistance when
(i) a constant current is passed through it
Answer:
For l = constant, heat produced H ∝ R
(ii) a constant potential difference is applied across its ends?
Answer:
For constant potential difference V, the heat produced, H ∝ \(\frac{1}{R}\)
Question 24.
Two wires of equal length, one of copper and the other of manganin have the same resistance. Which wire is thicker? (CBSE AI 2012)
Answer:
Manganin.
Question 25.
Two identical cells, each of emf E, having negligible internal resistance, are connected in parallel with each other across an external resistance R. What is the current through this resistance? (CBSE AI 2013)
Answer:
The current is l = E/R
Question 26.
Define temperature coefficient of resistivity. (CBSE Sample Paper 2018-2019)
Answer:
It is defined as the fractional change in resistivity per unit change in temperature.
Question 27.
A cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation of P.D. across R, versus R. (NCERT Exemplar)
Answer:
The graph is as shown.
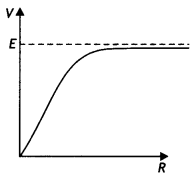
Current Electricity Important Extra Questions Short Answer Type
Question 1.
Why is a potentiometer preferred over a voltmeter for determining the emf of a cell? (CBSE Delhi 2016C)
Answer:
The potentiometer is based on the null method or it does not draw any (net) current from the cell and measures emf However, the voltmeter draws some current from the cell when connected across it, hence measures terminal voltage.
Question 2.
The figure shows the V – l graph for a parallel and series combination of two resistors A and B. Which line represents the parallel combination?
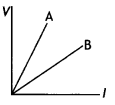
Answer:
For the same potential, the current is less in series combination than parallel combination. Therefore from the graph, it is apparent that the same potential current is less in A. Therefore B represents the parallel combination.
As, R = \(\frac{V}{l}\)
The slope of B > Slope of A
Question 3.
V – l graph for a given metallic wire at two temperatures is shown. Which of these is at a higher temperature?
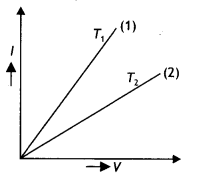
Answer:
At higher temperature resistance of a metallic wire is more or its conductance is low. Hence, graph (2) is at a higher temperature, i.e. T2 > T1.
Question 4.
In an experiment on a metre bridge, if the balancing length AC is ‘x’, what would be its value, when the radius of the metre bridge wire AB is doubled? Justify your answer. (CBSE AI 2011C)
Answer:
In a metre bridge, at the balance point we have
\(\frac{R_{1}}{R_{2}}=\frac{x}{100-x}\)
As R1 and R2 remain the same, x will also remain the same. It does not depend upon the diameter of the wire.
Question 5.
The emf of a cell is always greater than its terminal voltage. Why? Give reason. (CBSE Delhi 2013)
Answer:
When current passes through a cell, there is a drop in potential across it due to its internal resistance. This is called the lost volt. Thus terminal voltage is less than the emf of the cell.
Question 6.
Draw a graph showing the variation of resistivity with temperature for nichrome. Which property of nichrome is used to make standard resistance coils? (CBSEAI 2013C)
Answer:
The graph is as shown.
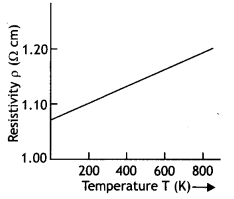
The property has a low-temperature coefficient of resistance.
Question 7.
Define the term ‘mobility’ for a charge carrier and state its SI unit.
Name the mobile charge carriers in
(i) an electrolyte,
(ii) a semiconductor and
(iii) an ionised gas. (CBSE Al 2015)
Answer:
Mobility is defined as the ratio of the drift velocity of the charge to the applied electric field.
(i) Anions and cations.
(ii) Electrons and holes
(iii) Free electrons.
Question 8.
Define the term current density of a metallic conductor. Deduce the relation connecting current density (J) and the conductivity (a) of the conductor, when an electric field E is applied to it. (CBSE AI 2015)
Answer:
Current density is defined as the current flowing per unit area of the conductor.
Mathematically current density is given by the expression J = \(\frac{l}{A}\)
But l = V/R and R = \(\frac{ρl}{A}\) = \(\frac{L}{σA}\). Substituting in the above relation, we have
J = \(\frac{l}{A}\) = \(\frac{V}{AL}\) × σA= \(\frac{V}{L}\) × σ = Eσ
Question 9.
(a) Define the terms ‘drift velocity’ and ‘relaxation time’ giving their physical significance.
Answer:
Drift Velocity: It is the average velocity of the free electrons with which they get drifted towards the positive terminal under the influence of the external field.
Significance: The net current flowing through any cross-section is controlled by drift velocity and there is no transport of charges in a direction perpendicular to the applied field. Relaxation Time (T): The average time between successive collisions of electrons or ions in a conductor is called the relaxation time.
Significance: It determines the drift velocity acquired by the electrons under the given applied electric force and also determines the electrical conductivity of a conductor at different temperatures.
(b) A conductor of length L is connected across a dc source of emf E. If the conductor is replaced by another of the same material and area of cross-section but of length 5L, by what factor will the drift velocity change? (CBSE2019C)
Answer:
In the first case:
Vd= \(\frac{e V}{m L}\)τ
In the second case:
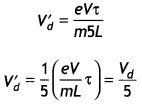
Thus we find that the drift velocity becomes \(\frac{1}{5}\) of its original value.
Question 10.
A cell of emf ‘E’ and internal resistance ‘r’ is connected across a variable resistor. ‘R’. Plot a graph showing the variation of terminal voltage ‘ V’ of the cell versus the current ‘l’. Using the plot, show how the emf of the cell and its internal resistance can be determined. (CBSE AI 2014)
Answer:
The graph is as shown.
For l = 0,V= E
The internal resistance can be found by using the expression
V = E – lr
For V = 0
E = lr
r = E/l
Question 11.
Two electric bulbs P and Q have their resistances in the ratio of 1: 2. They are connected in series across a battery. Find the ratio of the power dissipation in these bulbs. (CBSE AI, Delhi 2018)
Answer:
Given \(\frac{R_{\mathrm{p}}}{R_{\mathrm{Q}}}\) = \(\frac{1}{2}\)
Power dissipated \(\frac{P_{\mathrm{p}}}{P_{\mathrm{Q}}}=\frac{I^{2} R_{\mathrm{p}}}{I^{2} R_{\mathrm{Q}}}=\frac{1}{2}\)
Question 12.
A 10 V cell of negligible Internal resistance Is connected In parallel across a battery of emf 200 V and Internal resIstance 38 š as shown in the figure. Find the value of current in the circuit. (CBSE AI, Delhi 2018)
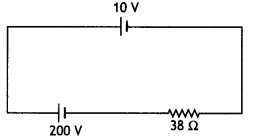
Answer:
Given ε1 = 10 V, r1 = 0, ε2 = 200 V, r2 = 38 Ω
The two cells send current in the opposite direction; therefore, net emf of the combination
E = 200 – 10 = 190V
Hence current in the circuit
l = \(\frac{E}{R}=\frac{190}{38}\) = 5 A
Question 13.
In a potentiometer arrangement for determining the emf of a cell, the balance point of the cell In an open circuit is 350 cm. When the resistance of 9 Ω Is used In the external circuit of the cell, the balance point shifts to 300 cm. Determine the internal resistance of the cell. (CBSE AI, Delhi 2018)
Answer:
Given L1 = 350 cm, L2 – 300 cm, R = 9 Ω, r = ? Using the expression
r = \(\left(\frac{L_{1}-L_{2}}{L_{2}}\right) R=\left(\frac{350-300}{300}\right)\) × 9 = 1.5 Ω
Question 14.
TWo bulbs are rated (P1 V) and (P2, V). If they are connected (i) in series and (ii) in parallel across a supply V, find the power dissipated in the two combinations in terms of P1 and P2. (CBSE Delhi 2019)
Answer:
Resistances of the two bulbs R1 = \(\frac{V^{2}}{P_{1}}\) and R2 = \(\frac{V^{2}}{P_{2}}\)
(i) Net resistance in series
Rs = R1 + R2 = \(\frac{V^{2}}{P_{1}}+\frac{V^{2}}{P_{2}}=V^{2}\left(\frac{P_{1}+P_{2}}{P_{1} P_{2}}\right)\)
(ii) Net resistance in parallel
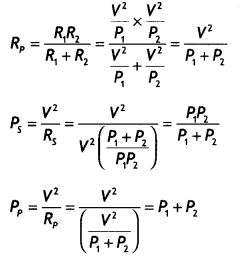
Question 15.
What is the advantage of using thick metallic strips to join wires in a potentiometer? (NCERT Exemplar)
Answer:
The metal strips have low resistance and need not be counted in the potentiometer Length l of the null point. One measures only their lengths along with the straight segments (of lengths 1 metre each). This is easily done with the help of centimetre rulings or metre ruler and leads to accurate measurements.
Question 16.
AB is a potentiometer wire (figure). If the value of R is increased, in which direction will the balance point J shift? (NCERT Exemplar)
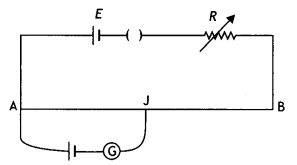
Answer:
If R is increased, the current through the wire will decrease. This will decrease the potential gradient across the potentiometer wire (k = V/L = lpRp/L). Hence more length of the wire will be required to balance the same cell. Therefore J will shift towards B.
Question 17.
While doing an experiment with a potentiometer (figure) it was found that the deflection is one-sided and
(i) the deflection decreased while moving from one end A of the wire to the end B;
(ii) the deflection increased while the jockey was moved towards the end B.
(iii) Which terminal + or -ve of the cell E1 is connected at X in case (i) and how is E1 related to E?
(iv) Which terminal of the cell E1 is connected at X in case (ii)? (NCERT Exemplar)
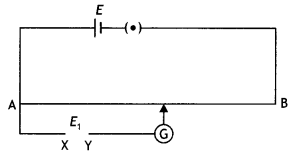
Answer:
(i) Positive terminal of E1 is connected at Xand E1 > E.
(ii) Negative terminal of E1 is connected at X.
Question 18.
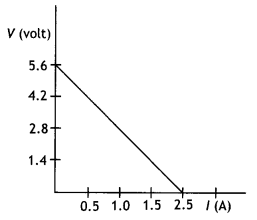
The circuit in the figure shows two cells connected in opposition to each other. Cell E1 is of emf 6 V and internal resistance 2 Ω; the cell E2 is of emf 4 V and internal resistance 8 Ω. Find the potential difference between the points A and B. (NCERT Exemplar)
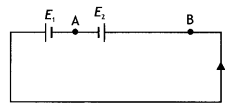
Answer:
The cells are connected in the opposite direction, therefore net emf in the circuit is
E = E1 – E2 = 6 – 4 = 2 V
Hence current in the circuit is
l = \(\frac{E}{R+r}\) = \(\frac{2}{10}\) = 0.2 A
P.D. across E1 = 6 – 0.2 × 2 = 5.6 V
P.D. across E2 = VAB = 4 + 0.2 × 8 = 5.6 V
Point B is at a higher potential than A
Current Electricity Important Extra Questions Long Answer Type
Question 1.
Explain the term ‘drift velocity’ of electrons in a conductor. Hence obtain the expression for the current through a conductor in terms of ‘drift velocity’. (CBSE AI 2013, 2013C)
Answer:
Drift velocity (Vd) is defined as the average velocity with which the free electrons get drifted inside a conductor under the effect of the electric field, opposite to the direction of the field.
Let n be the electrons per unit volume in the conductor. Here n is called the number density of electrons. Assume that all electrons move with the same drift velocity Vd. In a time interval dt, each electron moves a distance vdt. Now the volume of the cylinder covered by the electrons in time dt is
V = A vddt …(1)
and the number of electrons in this volume is
N = nV = nA vddt …(2)
If e is the charge on the electron, then charge flowing through the conductor in small time dt is
dQ = e(nA vddt) …(3)
Hence the current through the conductor is
l = \(\frac{dQ}{dt}\) = nAevd
Question 2.
Draw a plot showing the variation of resistivity of an (i) conductor and (ii) semiconductor, with the increase in temperature.
How does one explain this behaviour in terms of the number density of charge carriers and the relaxation time? (CBSE Delhi 2014C)
Answer:
The plots are as shown.
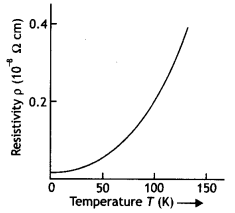
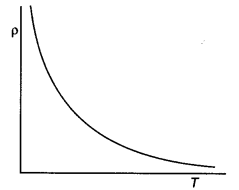
With a rise in temperature the average relaxation time for a conductor decreases and resistivity increases, while for a semiconductor the number density of charge carriers increases, hence the resistivity decreases.
Question 3.
State the two Kirchhoff’s rules used in electric networks. How are these rules justified? (CBSE Delhi 2015)
Answer:
The two rules are
Kirchhoff’s junction rule: The algebraic sum of currents meeting at a junction is zero.
Kirchhoff’s loop rule: The algebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero.
The two rules are justified as they are based on the law of conservation of charge and law of conservation of energy respectively.
Question 4.
(a) Deduce the relation between current l flowing through a conductor and drift velocity \(\vec{v}_{\mathrm{d}}\) of the electrons.
(b) Figure shows a plot of current ‘l’ flowing through the cross-section of a wire versus the time ‘t’. Use the plot to find the charge flowing in 10 s through the wire. (CBSE AI 2015C, 2016C)
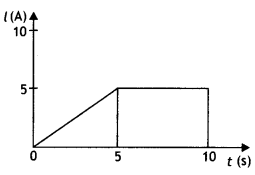
Answer:
Suppose there are n electrons per unit volume, where n is called the number density of electrons. Assume that all electrons move with the same drift velocity Vd. In a time interval dt, each electron moves a distance vddt. Now the volume of the cylinder covered by the electrons in time dt is
V = A vddt ….(1)
and the number of electrons in this volume is
N = nV=nA vddt …(2)
If e is the charge on the electron, then charge flowing through the conductor in small time dt is
dQ= e(nA vddt) …(3)
Hence the current through the conductor is
l = \(\frac{dQ}{dt}\) = vdenA
The area under the l – t curve gives the value of the charge
Q = 1/2 × 5 × 5 + (10 – 5) × 5 = 12.5 + 25
= 37.5 C
Question 5.
Answer the following:
(a) Why are the connections between the resistors in a metre bridge made of thick copper strips?
Answer:
The metal strips have low resistance;
hence their resistance does not come into play while calculating the unknown resistance.
(b) Why is it generally preferred to obtain the balance point in the middle of the metre bridge wire?
Answer:
It is done to reduce the index correction.
(c) Which material is used for the metre bridge wire and why? (CBSE Al 2014)
Answer:
Alloys are used due to their high resistivity.
Question 6.
(a) State the underlying principle of a potentiometer. Why is it necessary to (i) use a long wire, (ii) have a uniform area of cross-section of the wire and (iii) use a driving cell whose emf is taken to be greater than the EMFs of the primary cells?
Answer:
Principle: It is based on the principle that if a wire of uniform area of cross-section carries a constant current, the potential drop across any portion of the wire is directly proportional to the length of that portion of the wire.
The diagram is as shown.
First, the key K is inserted. This brings the cell of emf E1 in the circuit. The jockey is moved on the wire to obtain a balance point, i.e. a point on the wire where the galvanometer gives zero deflection. Let the balancing length be L1. Therefore by the potentiometer principle, we have
E1 ∝ L1 …(1)
Now, the key K2 is inserted. This brings the cell of emf E2 into the circuit. The jockey is again moved on the wire to obtain the balance point. Let the balancing length be L2. Then by potentiometer principle, we have
E2 ∝ L2 …(2)
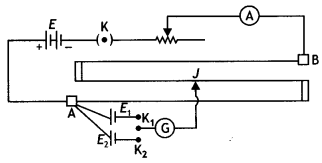
Dividing equations (1) by (2) we have
\(\frac{E_{1}}{E_{2}}=\frac{L_{1}}{L_{2}}\) …. (3)
Knowing the values of L1 and L2, the EMFs can be compared.
- The least count of the potentiometer is given by k = V/l, where l is the length of the potentiometer wire. The larger the value of l, the smaller is the least count. Hence a long wire is used so that there is more accuracy.
- If the area of cross-section is not uniform, the value of the potential ‘ gradient will not be the same along
the length of the wire. - The balance point will be obtained on the wire.
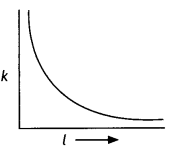
(b) In a potentiometer experiment, if the area of the cross-section of the wire increases uniformly from one end to the other, draw a graph showing how potential gradient would vary as the length of the wire increases from one end. (CBSE AI 2014C)
Answer:
k = \(\frac{V}{l}\) = \(\frac{lR}{l}\)
⇒ k ∝ \(\frac{1}{l}\)
Question 7.
Plot a graph showing the variation of current density (j) versus the electric field (E) for two conductors of different materials. What information from this plot regarding the properties of the conducting material, can be obtained which can be used to select suitable materials for use in making (i) standard resistance and (ii) connecting wires in electric circuits?
Electron drift speed is estimated to be of the order of mm s-1. Yet large current of the order of few amperes can be set up in the wire. Explain briefly. (CBSEAI 2015)
Answer:
We know that J = σE
Therefore the graph between J and E will be a straight line passing through the origin.
This is as shown.
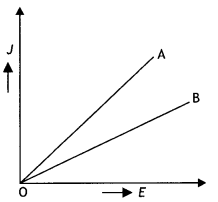
The slope of the graph = conductivity (σ)
Hence materiaL with Less slope (smaller conductivity) is used for making standard resistors and materiaL with greater slope (higher conductivity) for making connecting wires.
A large current can be set up in the wire because the electron number density is enormous, 1029 m-3.
Question 8.
The reading of the (ideal) ammeter, In the circuit shown here, equals:
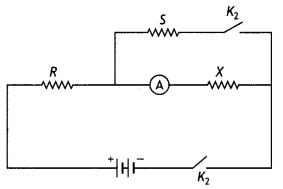
(i) l when key K1 is closed but key K2 is open.
Answer:
(i) Current l when K2 is open
l = \(\frac{ε}{R+X}\)
(ii) l/2 when both keys K1 and K2 are closed.
Find the expression for the resistance of X In terms of the resistances of R and S. (CBSE Delhi 2016C)
Answer:
Let current be l when both K1 and K2 are closed
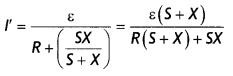
Current through X
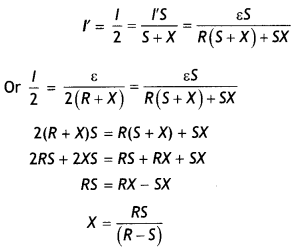
Question 9.
Define the current sensitivity of a galvanometer. Write Its S.I. unit. The figure shows two circuits each having a galvanometer and a battery of 3 V. When the galvanometers in each arrangement do not show any deflection, obtain the ratio R1/R2. (CBSE AI 2013)
Answer:
The current sensitivity of a galvanometer is defined as the deflection produced in the galvanometer per unit current passing through It. It is measured in div per ampere. In both cases the Wheatstone bridge is in the balanced state. Therefore we have
\(\frac{4}{R_{1}}=\frac{6}{9}\) Or R1 = 6 ohm
\(\frac{6}{12}=\frac{R_{2}}{8}\) Or R2 = 4 ohm
Therefore \(\frac{R_{1}}{R_{2}}=\frac{6}{4}=\frac{3}{2}\)
Question 10.
The following circuit shows the use of a potentiometer to measure the internal resistance of a cell, (i) When the key K is open, how does the balance point change, if the current from the driver cell decreases? (ii) When the key K is closed, how does the balance point change if R is increased, keeping the current from the driver cell constant?
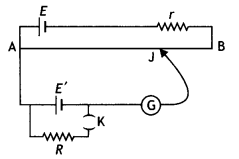
Answer:
(i) When the key K is open, a decrease in the current from the driver cell decreases the potential drop across the potentiometer wire. Therefore to balance the same emf again, more length of the wire will be required. Thus the balance point will shift towards point B.
(ii) When key K is closed and R is increased, it increases the terminal potential difference of the cell. Thus to balance the new terminal potential difference, more length of the wire will be required. Thus the balance point will shift towards point B.
Question 11.
(a) State, with the help of a circuit diagram, the working principle of a metre bridge. Obtain the expression used for determining the unknown resistance.
Answer:
(a) The experiment is based on the Wheatstone bridge principle.
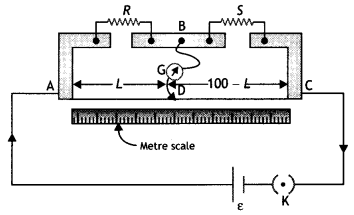
The connections are made as shown in the figure. A resistance R is introduced from the resistance box and the key K is closed. The jockey is moved on the wire to the point where there is no deflection in the galvanometer. In such case points, B and D are at the same potential. Point B is called the “null” point.
Let in this position AB = L cm and BC = (100 – L) cm. Therefore resistance of AB, i.e.
P ∝ L
and resistance of BC, i.e. Q ∝ (100 – L)
hence
\(\frac{P}{Q}=\frac{L}{100-L}\) …..(1)
In the balanced state by the Wheatstone bridge Principle we have
\(\frac{P}{Q}=\frac{R}{X}\) … (2)
Substituting equation (1) in equation (2) we have
\(\frac{R}{x}=\frac{L}{100-L}\) ….(3)
rewriting equation (3) we have
X = \(\left(\frac{100-L}{L}\right)\)R
(b) What happens if the galvanometer and cell are interchanged at the balance point of the bridge?
Answer:
There is no change in the position of the balance point if the galvanometer and the cell are interchanged.
(c) Why is it considered important to obtain the balance point near the mid-point of the wire? (CBSE Delhi 2011C)
Answer:
It is important to get the balance point near the mid-point of the wire because then the resistances in the four arms of the bridge are of the same order. The sensitivity of the bridge is maximum and the resistance is determined most accurately.
Question 12.
(a) Which material is used for potentiometer wire and why?
Answer:
The potentiometer wire is usually of constantan or manganin.
The material of the wire should have
- high specific resistance and
- low-temperature coefficient of resistance.
(b) How can the sensitivity of a potentiometer be increased? (CBSE Delhi 2011C)
Answer:
For greater sensitivity of the measurement, the fall of potential per cm should be less. The smaller the value of K, the greater will be the balancing length and the greater will be the accuracy of the measurement. For this, a wire of longer length should be taken or the current in the wire should be less.
Question 13.
Write two possible causes for one-sided deflection in a potentiometer experiment. (CBSE Delhi 2013)
Answer:
- The Emf of the auxiliary battery may be less than the emf of the test cell.
- The positive terminal of the test cell and the auxiliary cell may not be connected to the same point.
Question 14.
(a) Derive a relation between the internal resistance, emf and terminal potential difference of a cell from which current l is drawn. Draw V vs l graph for a cell and explain its significance.
Answer:
Consider the circuit shown.
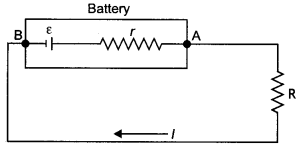
By Kirchhoff’s rules we have
E – lR – rl = 0
E – V – lr = 0
E = V + lr
The V-l graph is as shown.
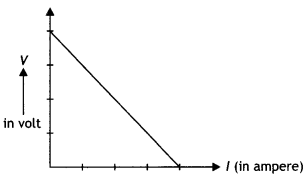
Significance of Graph: To find emf and internal resistance of the cell.
(b) A voltmeter of resistance 998 0 is connected across a cell of emf 2 V and internal resistance 2Q. Find the potential difference across the voltmeter and also across the terminals of the cell. Estimate the percentage error in the reading of the voltmeter.
Answer:
The diagram is as shown.
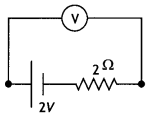
V= E – lr
998 × l = 2 – 2l
1000 l = 2
l = 0.002 A
Therefore,
V= 0.002 × 998= 1.996 V
Percentage error
\(\frac{2-1.996}{2}\) × 100 = \(\frac{0.004}{2}\) = 0.2%
Question 15.
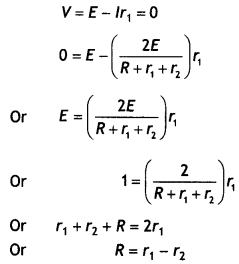
Two cells of the same emf E but internal resistance r1 and r2 are connected in series to an external resistor R (figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero? (NCERT Exemplar)
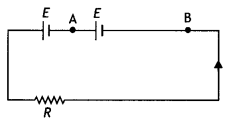
Answer:
Since the cells are connected in series,
total emf is
ET = E + E = 2E
Now current in the circuit Is
l = \(\frac{2 E}{R+r_{1}+r_{2}}\)
For terminal potential difference across the first cell to be zero we have
Question 16.
Two cells of EMFs ε1 and ε2 and Internal resistances r1 and r2 respectively are connected in parallel. Obtain expressions for the equivalent
(i) resistance and
(ii) emf of the combination (CBSE Delhi 2018C, 2019C)
Answer:
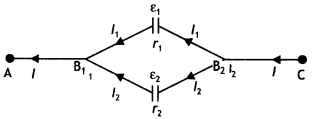
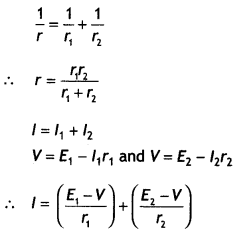
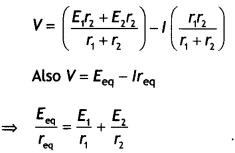
Question 17.
Using Kirchhoff’s rules, calculate the potential difference between B and D In the circuit diagram as shown in the figure. (CBSE Delhi 2018C)
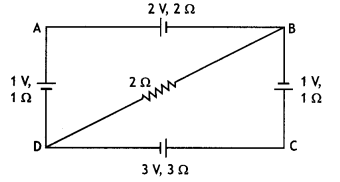
Answer:
Using Kirchhoff’s voLtage ruLe, we have:
For Loop DABD
l1 × 1 + (1) + (-2) + 2l1 + 2(l1 + l2) = 0
Or 5l1 + 2l2 = 1 …. (i)
For Loop DCBD
l2 × 3 + (3) + (-1) + l2 + 2(l1 + l2) = 0
Or 2l1 + 6 l2 = -2 …. (ii)
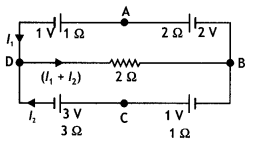
Solving (i) and (ii), we get
l1 = \(\frac{5}{13}\)A
l2 = \(\frac{-6}{13}\)A
∴ Current through DB = l1 + l2 = \(\frac{-1}{13}\)A
∴ P.D. between B and D = 0.154 V
Question 18.
Define the term resistivity of a conductor. Give its SI unit. Show that the resistance R of a conductor Is given by \(\frac{m L}{n e^{2} A \tau}\)where the symbols have their usual meaning.
Answer:
The resistivity of a conductor is the resistance of the conductor of unit length and unit cross-sectional area.
Let Vd be the drift velocity of the electrons, then its relation with the electric field is
Vd = \(-\frac{e E}{m}\)τ …..(1)
Let V be the potential difference applied across the two ends of a conductor of length L and area of cross-section A, then
E = \(\frac{-V}{L}\) …..(2)
Substituting equation (1) in (2) we have
Vd = \(\frac{\mathrm{eV}}{\mathrm{mL}}\)τ ….(3)
Also l = neAVd ….(4)
Substituting equation (3) in equation (4),
we have
l = neA\(\left[\frac{e V}{m L} \tau\right]=\left[\frac{n e^{2} A \tau}{m L}\right]\)V ….(5)
Comparing with Ohm’s “Law”, i.e
l = \(\frac{V}{R}\) …. (6)
we have
R = \(\left[\frac{m L}{n e^{2} A \tau}\right]\) ….(7)
Question 19.
The given figure shows a network of resistances R1, R2, R3 and R4.
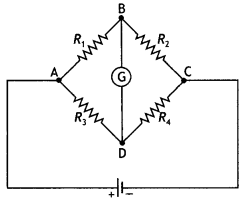
Using Kirchhoff’s laws, establish the balance condition for the network. (CBSEAI 2015)
Answer:
Consider the diagram as shown below.
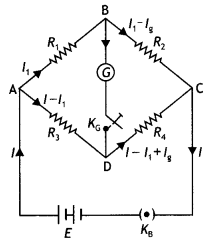
Now applying Kirchhoff’s Loop rule to the closed Loop ABDA, we have
– l1R1 – lgG + (l – l1) R3 = 0 ….(1)
Again applying Kirchhoff’s Loop rule to closed-loop BCDB, we have
– (l1 – lg)R2 + (l – l1 + lg)R4 + lgG = 0 …(2)
The values of R1, R2, R3 and R4 are so adjusted that the galvanometer gives zero deflection. This means that both B and D will be at the same potential and hence no current will flow through the galvanometer,
i.e. lg = 0. In this situation, the Wheatstone bridge is said to be balanced. Putting lg = 0 in equations (1) and (2) we have
– l1R1 + (l – l1) R3 = 0
and
-l1R2 + (l – l1)R4 = 0 …(4)
Rewriting the above two equations we have
– l1R1 = (l – l1) R3 ….(5)
and
– l1R2 + (l – l1)R4 ….(6)
Dividing the above equations we have
\(\frac{R_{1}}{R_{2}}=\frac{R_{3}}{R_{4}}\) … (7)
The above expression gives the condition for the balance of a Wheatstone bridge.
Question 20.
Draw a circuit diagram of a potentiometer. State its working principle. Derive the necessary formula to describe how it is used to compare the EMFs of the two cells. (CBSE AI 2015C)
Answer:
PRINCIPLE: It is based on the principle that if a wire of uniform area of cross-section carries a constant current, the potential drop across any portion of the wire is directly proportional to the length of that portion of the wire.
The diagram is as shown.
First, the key K is inserted. This brings the cell of emf E1 into the circuit. The jockey is moved on the wire to obtain a balance point, i.e. a point on the wire where the galvanometer gives zero deflection. Let the balancing length be L1. Therefore by the potentiometer principle, we have
E1 ∝ L1 …(1)
Now, the key K2 is inserted. This brings the cell of emf E2 into the circuit. The jockey is again moved on the wire to obtain the balance point. Let the balancing length be L2. Then by potentiometer principle, we have
E2 ∝ L2 …(2)

Dividing equations (1) by (2) we have
\(\frac{E_{1}}{E_{2}}=\frac{L_{1}}{L_{2}}\) …. (3)
Knowing the values of L1 and L2, the EMFs can be compared.
Question 21.
(i) Define the term ‘conductivity’ of a metallic wire. Write its SI unit.
Answer:
The property of a material that allows a flow of electrons between two points of the material when a potential difference is applied between these two points is called the conductivity of a wire. SI unit of conductivity: siemens per metre.
(ii) Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in terms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E. (CBSE At 2018, Delhi 2018)
Answer:
Drift velocity of electrons in a conductor is given as
Vd = eEτ/m …(1)
Small distance covered in time
Δt = VdΔt
Amount of charge passing through the area A in time Δt, q = lΔt
Δt = neAVdΔt
or l = neAVd …(2)
where
n → Number of free electrons per unit volume or number density
Now from equations (1) and (2), we get
l = ne2AτE/m …(3)
Since resistivity of a conductor is given as
ρ = m/ne2τ
Now, we know that the conductivity of a conductor is mathematically defined as the reciprocal of resistivity of the conductor. Thus,
σ = \(\frac{1}{ρ}\) …(4)
where σ = conductivity of the conductor. Thus, from equations (3) and (4), we get
σ = ne2τ/m ….(5)
Now, from equations (3) and (5), we have
lA = σE …(6)
and current density is given as
J = lA
Thus, J = σE
Question 22.
(a) You are required to select a carbon resistor of resistance of 56 kΩ ± 10% from a shopkeeper. What would be the sequence of colour bands required to code the desired resistor?
Answer:
Number 5 corresponds to green, No. 6 corresponds to blue, 103 corresponds to orange and 10% corresponds to silver.
∴ The sequence of Colours is
Green, blue, orange, silver
(b) Write two characteristic properties of the material of a metre bridge wire.
Answer:
Metre bridge wire must have
- High resistivity
- Low-temperature coefficient of resistivity
(c) What precautions do you take to minimise the error in finding the unknown resistance of the given wire? (CBSE2019C)
Answer:
To minimise the error in determining the resistance of a wire, the
- The wire should be of uniform thickness
- The balance point should be near the midpoint of the wire
Question 23.
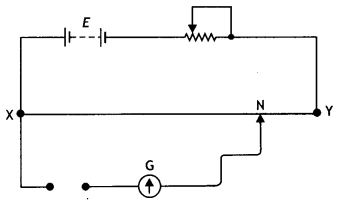
The diagram below shows a potentiometer set-up. On touching the jockey near the end X of the potentiometer wire, the galvanometer pointer deflects to left. On touching the jockey near to end Y of the potentiometer, the galvanometer pointer again deflects to left but now by a larger amount. Identify the fault in the circuit and explain, using appropriate equations or otherwise, how it leads to such a one¬sided deflection. (CBSE Sample Paper 2018-19)
Or
The following circuit was set up in a metre bridge experiment to determine the value X of unknown resistance.
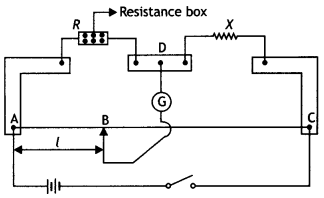
(i) Write the formula to be used for finding X from the observations. 39.5 cm from end A, when the resistor Y is 12.5 Ω. Determine the resistance of X. Why are the connections between resistors in a Wheatstone or metre bridge made of thick copper strips?
(ii) If the resistance R is increased, what will happen to balance length?
Answer:
The positive of E1 is not connected to terminal X.
In Loop XGNX,
E1 – VG + E = 0
VG = E1 + EXN
VG = E1 + kl
So, VG (or deflection) Will be maximum when l is maximum, i.e. when Jockey Is touched near the end Y. Also, VG (or deflection) Will, be minimum when l is minimum, i.e. when a jockey is touched near end X.
Or
(i) X = (100 – l) R/l
(ii) The balancing Length wilt increase.
Question 24.
(i) In a metre bridge as shown, the balance point is found to be at 39.5 cm from the end A, when the resistor Y is 12.5. Determine the resistance of X. Why are the connections between resistors In a Wheatstone or metre bridge made of thick copper strips?
(ii) Determine the balance point of the bridge above if X and Y are interchanged.
(iii) What happens if the galvanometer and cell are interchanged at the balance point of the bridge? Would the galvanometer show any current? (NCERT)
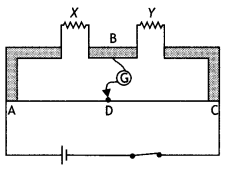
Answer:
(i) Given L1 = 39.5 cm and L2 =100 – 39.5 = 60.5 cm, Y=12.5Q, X=?
Using the Wheatstone bridge principle we have
\(\frac{39.5}{60.5}=\frac{X}{12.5}\) or X = 8.2 Ω
The connections between resistors in a Wheatstone or metre bridge are made of thick copper strips to minimise the resistance of the connection which are not accounted for in the bridge formula.
(ii) If X and Y are interchanged, then
\(\frac{L}{(100-L)}=\frac{12.5}{8.2}\); solving for L we have
L = 60.4 cm from point A.
(iii) When the galvanometer and cell are interchanged, the condition for the balance of the bridge remains satisfied. Hence galvanometer will not show any current.
Question 25.
The figure below shows a potentiometer with a cell of 2.0 V and internal resistance of 0. 40 Ω maintaining a potential drop across the resistor wire AB. A standard cell that maintains a constant emf of 1.02 V (for very moderate currents up to a few mA) gives a balance point at 67.3 cm length of the wire. To ensure very low currents drawn from the standard cell, very high resistance of 600 kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf e and the balance point found similarly, turns out to be at 82.3 cm length of the wire.
1. What is the value of e?
2. What purpose does the high resistance of 600 kΩ have?
3. Is the balance point affected by this high resistance?
4. Is the balance point affected by internal resistance?
5. Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0 V instead of 2.0 V?
6. Would the circuit work well for determining an extremely small emf, say of the order of a few mV (such as the typical emf of a thermo-couple)? If not, how will you modify the circuit?
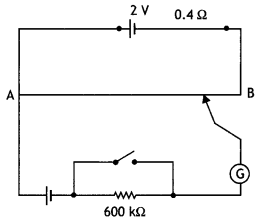
Answer:
1. Given ε1 = 1.02 V, L1 = 67.3 cm, L2 = 82.3 cm, ε2 = ?
By potentiometer principle we have
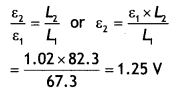
2. This resistance reduces the current through the galvanometer when the movable contact (a jockey) is far away from the balance point. This, in turn, protects the galvanometer from the damage likely to be caused by the high current.
3. There is no effect of this resistance on the balance point.
4. There is no effect.
5. In case, the driving emf is smaller than the emf to be measured, the balance point cannot be found on the potentiometer wire.
6. In such a case, the balance point will be very close to the end giving a very large error in the measurement of e. If resistance is placed in series with the wire AB such that the potential drop across AB is only slightly larger than the emf to be measured, the balance point will be found on a larger length. This will make the error very small.
Numerical Problems:
Formulae for solving numerical problems.
- The mobility of electrons is given by μ = \(\frac{V_{d}}{E}=\frac{e \tau}{m}\)
- By Ohm’s law, l = \(\frac{V}{R}\) and J = σE
- The current density is J = \(\frac{l}{A}\) = nevd
- Theresistanceofawireis R = ρ\(\frac{L}{A}\) = \(\left[\frac{m L}{n e^{2} A \tau}\right]\)
- The resistivity of a wire is ρ = \(\frac{m}{n e^{2} \tau}\)
- The resistance of a wire at t°C is R = R0 (1 + αt)
- In parallel combination \(\frac{1}{R_{p}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}\)
- In series combination Rs = R1 + R2 + R3 + ……..
- Ratio of resistances in series and parallel \(\frac{R_{\mathrm{s}}}{R_{\mathrm{p}}}\) = n2
- The Wheatstone bridge principle is \(\frac{P}{Q}=\frac{R}{S}\)
- V = E – lr, where V is the terminal potential difference, E is emf and r is the internal resistance of the cell.
- The internal resistance of a cell is r = \(\frac{(E-V) R}{V}=\frac{\left(L_{1}-L_{2}\right) R}{L_{2}}\)
Question 1.
A cell of emf ‘E’ and internal resistance ‘r’ is connected across a variable load resistor R. Draw the plots of the terminal voltage V versus (i) R and (ii) the current l.
It is found that when R = 4 Ω the current is 1 A and when R is increased to 9 Ω, the current reduces to 0.5 A. Find the values of the emf E and internal resistance r. (CBSE Delhi 2015)
Answer:
The plots are as shown
Here l1 = 1.0 A, R1 =4 ohm, l2 = 0.5 A, R2 =9 ohm
Using the equation l = \(\frac{E}{(R+r)}\) Or E = l(R + r)
we have
1.0 × (4 + r) = 0.5 × (9 + r)
Solving the above equation for r we have r = 1 ohm
Also E = 0.5 (9 + 1) = 5 V
Question 2.
A wire of resistance R, length l and area of cross-section A is cut into two parts, having their lengths in the ratio 1:2. The shorter wire is now stretched till its length becomes equal to that of the longer wire. If they are now connected in parallel, find the net resistance of the combination. (CBSE Al 2019)
Answer:
Since the wires are cut in the ratio of 1:2 therefore,
Resistance of the shorter wire R1 = \(\frac{R}{3}\) and
Resistance of the longer wire R2 = \(\frac{2R}{3}\)
Since the shorter wire is stretched to make it equal to the longer wire therefore, it is stretched by n = 2 times its length. Hence New resistance of the shorter wire
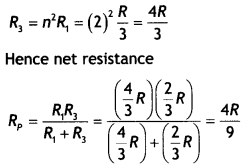
Question 3.
In the figure, a long uniform potentiometer wire AB is having a constant potential gradient along its length. The null points for the two primary cells of EMFs ε1 and ε2 connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A. Find (i) ε1/ε2 and (ii) position of null point for the cell ε1. How is the sensitivity of a potentiometer increased? (CBSE Delhi 2012)
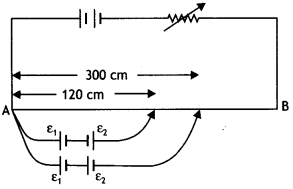
Answer:
From the diagram we have
\(\frac{\varepsilon_{1}-\varepsilon_{2}}{\varepsilon_{1}+\varepsilon_{2}}=\frac{120}{300}=\frac{2}{5}\)
Or
5ε1 – 5ε2 = 2ε1 + 2ε2
Solving we have
\(\frac{\varepsilon_{1}}{\varepsilon_{2}}=\frac{7}{3}\) ….(1)
Also let L be the balancing length for cell of emf ε1, then
\(\frac{\varepsilon_{1}}{\varepsilon_{1}+\varepsilon_{2}}=\frac{L}{300}\)
Using equation (1) we have
\(\frac{\varepsilon_{1}}{\varepsilon_{1}+\frac{3}{7} \varepsilon_{1}}=\frac{L}{300}\)
Solving for L we have L = 210 cm
The sensitivity of a potentiometer can be increased by increasing the length of the potentiometer wire.
Question 4.
The network PQRS, shown in the circuit diagram, has batteries of 4 V and 5 V and negligible internal resistance. A milli- ammeter of 20 Ω resistance is connected between P and R. Calculate the reading in the milliammeter. (CBSE AI 2012C)
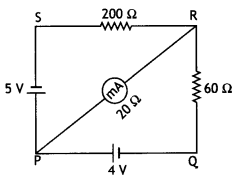
Answer:
Using Kirchhoff’s junction rule to distribute current we have
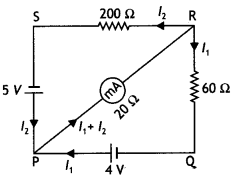
Consider the loop SRPS, by Kirchhoff’s loop rule we have
200 l2 + 20 (l1 + l2 ) – 5 = 0 …(1)
Or
220 l2 + 20 l1 = 5 …(2)
Consider the loop PRQP, by Kirchhoff’s loop rule we have
– 60 l1 + 4 – 20 (l1 + l2) = 0 …(3)
80 l1 + 20 l2 =4 …(4)
Multiplying equation (2) by (4) we have
880 l2 + 80 l1 = 20 …(5)
Subtracting equation (4) from equation (5)
we have
860 l2 = 16 or l2 = 4/215 A
Substituting in equation (4) we have
l1 = \(\frac{39}{860}\)A
Therefore reading of the milliammeter is
l1+ l2 = \(\frac{4}{215}+\frac{39}{860}\) = 0.063 A = 63 mA
Question 5.
A set of ‘n’ identical resistors, each of resistance ‘R’ when connected in series have an effective resistance ‘X’. When they are connected in parallel, their effective resistance becomes ‘Y’. Find out the product of X and Y. (CBSEAI2019) Answer:
In series
Rs = R1 + R2 + R3 + ……
Rs = X = R + R + R + …. upto n
X=nR
In Parallel
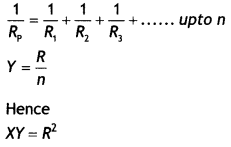
Question 6.
In the following circuit, a metre bridge is shown in its balanced state. The metre bridge wire has a resistance of 1 ohm per centimetre. Calculate the value of the unknown resistance X and the current drawn from the battery of negligible internal resistance.
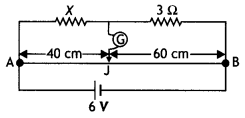
Answer:
Using the Wheatstone bridge principle we have
\(\frac{40}{60}=\frac{X}{3}\)
or X = 2 Ω
Now total resistance of the combination is
R = \(\frac{5 \times 100}{5+100}=\frac{500}{105}\) = 4.76 Ω
Current drawn is
l = V/R = 6/4.76 = 1.26 A
Question 7.
Calculate the electrical conductivity of the material of a conductor of length 3 m, area of cross-section 0.02 mm2 having a resistance of 2 ohms.
Answer:
Given L = 3 m,
A = 0.02 mm2 = 0.02 × 10-6 m2
R = 2 ohm.
Using the equation
R = \(\frac{ρL}{A}\)
Or
ρ = \(\frac{RA}{L}\)
σ = \(\frac{L}{AR}\) = \(\frac{3}{0.02 \times 10^{-6} \times 2}\) = 7.5 × 107 Sm-1
Question 8.
A potential difference of 2 volts is applied between points A and B has shown in the network drawn in the figure. Calculate (i) equivalent resistance of the network across the points A and B and (ii) the magnitudes of currents in the arms AFCEB and AFDEB.
Answer:
The circuit can be redrawn as shown below.
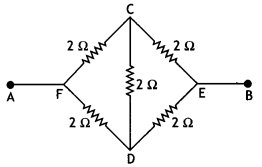
As seen the circuit is a balanced Wheatstone bridge; therefore the resistance in the arm CD is superfluous.
(i) Resistance of arm FCE = 2 + 2 = 4 Ω
Resistance of arm FDE = 2 + 2 = 4 Ω
Hence net resistance of the circuit between A and B is
R = \(\frac{4 \times 4}{4+4}=\frac{16}{8}\) = 2 Ω
(ii) current in the arm AFCEB
l = V/R = 2/4 = 0.5 A
Current in the arm AFDEB
l = V/R = 2/4 = 0.5 A
Question 9.
A cell of emf E and internal resistance ‘r’ gives a current of 0.8 A with an external resistor of 24 ohms and a current of 0.5 A with an external resistor of 40 ohms.
Calculate
(i) emf E and
(ii) internal resistance ‘r’ of the cell.
Answer:
Given l1 = 0.8 A, R1 = 24 ohm l2 = 0.5 A, R2 = 40 ohm
Using the equation
E = l(R + r) we have
0.8 × (24 + r) = 0.5 × (40 + r)
Solving for r we have r = 2.67 ohm
Also E = 0.5( 40 + 2.67) = 21.3 V
Question 10.
In the circuit diagram of the metre bridge given below, the balance point is found to be at 40 cm from A. The resistance of X is unknown and Y is 10 ohms.
(i) Calculate the value of X;
(ii) if the positions of X and Y are interchanged in the bridge, find the position of the new balance point from A; and
(iii) if the galvanometer and the cell are interchanged at the balance point, would the galvanometer show any current.
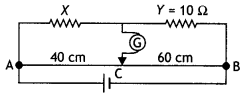
Answer:
(i) Using the Wheatstone bridge principle we have
\(\frac{40}{60}=\frac{X}{10}\)
Or
X = 6.67 Ω
(ii) If X and Y are interchanged then
\(\frac{L}{(100-L)}=\frac{10}{6.67}\) solving for L we have
L = 59.9cm
(iii) The ga(vanometer will not show any current.
Question 11.
The length of a potentiometer wire is 600 cm and it carries a current of 40 mA. For a cell of emf 2.0 V and internal resistance 10 ohms, the null point is found to be at 500 cm. If a voltmeter is connected across the cell, the balancing length is decreased by 10 cm. Find (i) the resistance of the whole wire, (ii) reading of the voltmeter and (iii) resistance of the voltmeter.
Answer:
Here total length of potentiometer wire L = 600 cm, current flowing
l = 40 mA = 0.04 A,
Emf of cell E = 2 V,
Internal resistance of cell r = 10 Ω, balancing length for cell l = 500 cm
(i) Since ε = kl
k = \(\frac{\varepsilon}{l}=\frac{2}{500}\) , V = kl
∴ V = \(\frac{2}{500}\) × 600 = 2.4 V
Therefore resistance of the potentiometer wire =\(\frac{V}{l}=\frac{2.4}{0.04}\) = 60 Ω.
(ii) With voltmeter connected across the cell, balancing Length
L’ = l – 10 = 500 – 10 = 490cm
Therefore, potential difference, i.e. reading of voltmeter,
= \(\frac{L^{\prime}}{L} \times V=\frac{490}{600}\) × 2.4 = 1.96 V
(iii) Let resistance of the voltmeter be R,
R = \(\frac{V}{l}=\frac{1.96}{0.04}\) = 49 Ω
R = 49 ohm
Question 12.
Find the value of the unknown resistance X in the following circuit, if no current flows through the section AO. Also, calculate the current drawn by the circuit from the battery of emf 6 V and negligible internal resistance.
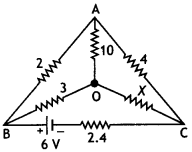
Answer:
If no current flows through the section AO, the given circuit is an example of a balanced Wheatstone bridge. The circuit can be redrawn as
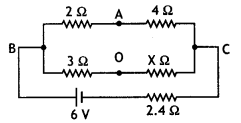
Then \(\frac{2}{4}=\frac{3}{X}\)
Or
X = \(\frac{3 \times 4}{2}\) = 6 Ω
Now 2 Ω and 4 Ω are in series and 3 Ω and 6 Ω are also in series; so the circuit becomes
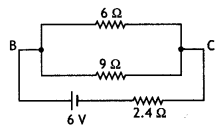
Hence total resistance of the circuit
R = 2.4 + \(\left(\frac{9 \times 6}{15}\right)\) = 6 Ω
Hence current drawn from the battery
l = V/R = 6/6 = 1 A
Question 13.
In the given circuit, calculate the value of current in a 4.5-ohm resistor and indicate its direction. Also, calculate the potential difference across each cell.
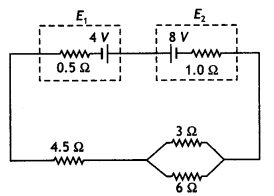
Answer:
The effective resistance of 3 ohms and 6-ohm resistors in parallel is
R = \(\frac{3 \times 6}{3+6}\) =2Q
Hence the resistance of the entire circuit
R = 2 + 4.5 + 0.5 + 1 = 8 ohm
Effective emf of the circuit E = 8 – 4 = 4 V.
Therefore current through the circuit and hence through the 4.5-ohm resistor is
l = E/R = 4/8 = 0.5 A.
The direction of the current is from cell E2 towards cell E1.
The potential difference across 8 V battery
V = E – lr = 8 – 0.5 × 1 = 7.5 V
The potential difference across 4 V battery
V = E + lr = 4 + o.5 × 0.5 = 4.25 V
Question 14.
Potentiometer wire PQ of 1-metre length is connected to a standard cell E1. Another cell, E2 of emf 1.02 V, is connected as shown In the circuit diagram with a resistance ‘r’ and a switch, S. with the switch open, the null position is obtained at a distance of 51 cm from P.
Calculate (i) the potential gradient of the potentiometer wire and
(ii) the emf of the cell E1.
(iii) When switch S is closed, will the null point move towards P or towards Q? Give a reason for your answer.
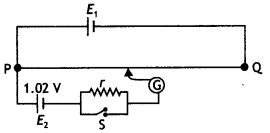
Answer:
Here E2 = 1.02V and with switch open L = 51 cm
(i) Potential gradient k = E/L
= 1.02 /51 = 0.02 V cm-1
(ii) As total length of potentiometer wire L = 1 m = 100 cm
Therefore E1 = kL = 0.02 × 100 = 2 V
(iii) When switch S is closed, the null point will remain unaffected because cell E2 is even now in an open circuit and no current is being drawn from it.
Question 15.
Three identical resistors when connected in series to a dc source dissipate a power of X watt. If these resistors are connected in parallel to the same dc source, what will be the power dissipation in this case?
Answer:
Given Ps = X, Rs = 3R, Rp = R/3
Power in series Ps = \(\frac{V^{2}}{R_{s}}\) or X = \(\frac{V^{2}}{3 R}\) or 3X = \(\frac{V^{2}}{R}\)
When resistors are connected In parallel, we have
Pp = \(\frac{V^{2}}{R_{p}}=\frac{V^{2}}{R / 3}=\frac{3 V^{2}}{R}\) = 3 × 3X = 9X
Question 16.
A heater coil is rated 100W, 200V. It is cut into two Identical parts. Both parts are connected In parallel, to the same source of 200 V. Calculate the energy liberated per second in the new combination.
Answer:
The resistance of the coil
R = \(\frac{V^{2}}{P}=\frac{(200)^{2}}{100}\) = 400 Ω
When the coil is cut into two equal halves, the resistance of each half becomes 200 ohms.
When these two parts are connected in parallel, the resultant resistance is
Rp = \(\frac{200 \times 200}{200+200}\) = 100 Ω
Now energy Liberated
H = \(\frac{V^{2}}{R_{\mathrm{p}}}=\frac{(200)^{2}}{100}\) = 400 Ω
Question 17.
AB is a 1 m long uniform wire of 10 Ω resistance. The other data are as shown in the circuit diagram given in the figure below. Calculate (i) potential gradient along with AB and (ii) length AO of the wire, when the galvanometer shows no deflection.
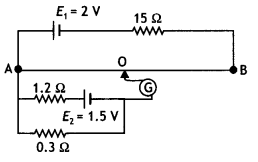
Answer:
Emf of battery E1 = 2 V.
Resistance of potentiometer R = 10 Ω,
Resistance joined in series R1 = 15 Ω and
Length of potentiometer wire L = 1 m = 100 cm
(i) Potential gradient
k = \(\frac{E_{1} R}{\left(R+R_{1}\right) L}=\frac{2 \times 10}{(10+15) \times 100}\) = 0.008 Vcm-1
(ii) Current through 0.3 Ω resistance due
to cell E1, l = \(\frac{1.5}{1.2+0.3}\) = 1 A
Potential difference across 0.3 Ω resistance = l × 0.3 = l × 0.3 = 0.3 V
∴ Length AO = \(\frac{\text { Potential difference }}{\text { Potential gradient }}\) = 37.5 cm
Question 18.
In a potentiometer, a standard cell of emf 5V and of negligible resistance maintains a steady current through the potentiometer wire of length 5 m. Two primary cells of EMFs E1 and E2 are joined in series with (a) the same polarity and (b) opposite polarity. The combination Is connected through a galvanometer and a jockey to the potentiometer. The balancing lengths In the two cases are found to be 350 cm and 50 cm, respectively.
(i) Draw the necessary circuit diagram.
(ii) Find the value of the EMFs of the two cells.
Answer:
(i) The circuit diagram is as shown below.
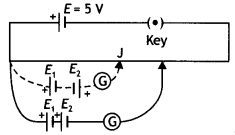
(ii) With cells E1 and E2 joined in series with the same polarity, the resultant emf
E = E1 + E2 and
Balancing Length L = 350 cm.
With celLs joined in series with opposite polarity, the resuLtant emf
E’ = E1 – E2 and
Balancing Length L = 50 cm.
Moreover, the potentiaL gradient
k = \(\frac{V}{L}=\frac{5 \mathrm{~V}}{5 \mathrm{~m}}=\frac{5 \mathrm{~V}}{500 \mathrm{~cm}}\) = 0.01 Vcm-1
Therefore
E1 + E2 = kL = 0.01 × 350 = 3.5 V and
E1 – E2 = kL = 0.01 × 50 = 0.5 V
Solving for the two EMFs we get E1 = 2V and E2 = 1.5 V
Question 19.
Using Kirchhoff’s rules, calculate the current through the 40 Q and 200 resistors in the following circuit:
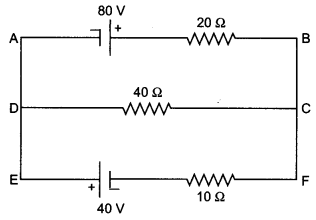
Or
What is the end error in a metre bridge? How is it overcome? The resistances in the two arms of the metre bridge are R = 5 Ω and S respectively. When the resistance S is shunted with equal resistance, the new balance length found to be 1.5 L1, where L1 is the initial balancing length. Calculate the value of S. (CBSE Delhi 2019)
Answer:
The distribution of current is as shown
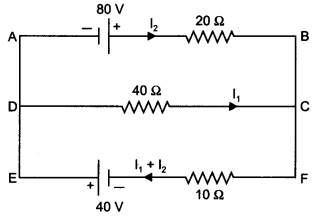
In loop ABCDA
+ 80 – 20 l2 + 40 l1 = 0
4 = l2 – 2 l1
In loop DCFED
– 40 l1 – 10(l1 + l2) + 40 = 0
-50 l1 – 10 l2 + 40 = 0
5 l1 + l2 = 4
Solving these two equations
l1 = 0 A and
l2 = 4 A
Or
The end error, in a meter bridge, is the error arising due to
(i) Ends of the wire not coinciding with the 0 cm/100 cm mark on the meter scale.
(ii) Presence of contact resistance at the joints of the meter bridge wire with the metallic strips.
It can be reduced/overcome by finding balance length with two interchanged positions of R and S and taking the average value of ‘S’ from these two readings.
For a metre bridge, we have
\(\frac{R}{S}=\frac{L}{100-L}\)
For the two given conditions, we have
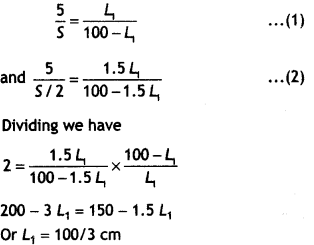
Putting this value in equation (1) we have S = 10 Ω.
Question 20.
A 10 m long wire of uniform cross-section and 20-ohm resistance is used in a potentiometer. The wire is connected in series with a battery of 5 V along with an external resistance of 480 ohms. If an unknown emf E is balanced at 6.0 m length of the wire, calculate:
(i) the potential gradient of the potentiometer wire
(ii) the value of unknown emf E.
Answer:
Total resistance of the circuit
R = 20 + 480 = 500 ohm
Therefore current through the potentiometer
l = \(\frac{V}{R}=\frac{5}{500}\) = 0.01 A
Now potential drop across the potentiometer wire of 20 ohm = 20 × 0.01 = 0.2 V
(i) Potential gradient
\(\frac{V}{L}=\frac{0.2}{10}\) = 0.02 Vm-1
(ii) Unknown emf = balancing length × potential gradient = 6 × 0.02 = 0.12 V
Question 21.
In a potentiometer arrangement, a cell of emf 1.20 volt gives a balance point at 30 cm length of the wire. This cell is now replaced by another cell of unknown emf. If the ratio of the EMFs of the two cells is 1.5, calculate the difference in the balancing length of the potentiometer wire in the two cases.
Answer:
Given E1 = 1.20 V, L1 = 30 cm, E2 = ?,
E1/E2 = 1.5, L1 – L2 = ?
Now \(\frac{E_{1}}{E_{2}}=\frac{L_{1}}{L_{2}}\) or 1.5 = \(\frac{30}{L_{2}}\) or L2 = 20 cm
Therefore L1 – L2 = 30 – 20 = 10 cm
Question 22.
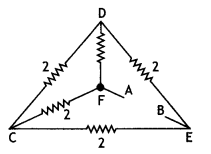
A uniform wire of resistance 12 Ω is cut into three pieces so that the ratio of the resistances R1: R2: R3 = 1: 2: 3 and the three pieces are connected to form a triangle across which a cell of emf 8 V and internal resistance 1 Ω is connected as shown. Calculate the current through each part of the circuit. (CBSE A! 2013C)
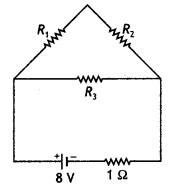
Answer:
Value of the three resistances are
R1 = \(\frac{1}{6}\) × 12 = 2 Ω,
R2 = \(\frac{2}{6}\) × 12 = 4 Ω
and R3 = \(\frac{3}{6}\) × 12 = 6 Ω
Now R1 and R2 are connected in series, therefore we have
R = R1 + R2 = 2 + 4 = 6 Ω
Now R and R3 are connected in parallel, therefore net resistance
Rp = \(\frac{R R_{3}}{R+R_{3}}=\frac{6 \times 6}{6+6}\) = 3 Ω
Now Rp and the internal resistance of the cell are connected in series, therefore net resistance of the circuit is
RN = Rp + 1 = 3 + 1 = 4 Ω
Hence current in the circuit is
l = V/RN = 8/4 = 2 A
This is equally divided amongst R1, R2 and R3. Therefore current through all the three resistors is 1 A.
Question 23.
A battery of emf E and internal resistance r when connected across an external resistance of 12 ohms produces a current of 0.5 A. When connected across a resistance of 25 ohms it produces a current of 0.25 A. Determine the (i) emf and (ii) internal resistance of the cell. (CBSEAI2013C)
Answer:
Here l1 = 0.5 A, R1 =12 ohm, l2 = 0.25 A, R22 = 25 ohm
Using the equation l = \(\frac{E}{(R+r)}\) or E = l(R + r)
we have
0. 5 × (12 + 1) = 0.25 × (25 + r)
Solving the above equation for r we have
r = 1 ohm
Also E = 0.5 (12 + 1) = 6.5 V
Question 24.
The resistance of the platinum wire of a platinum resistance thermometer at the ice point is 5 Ω and at steam, the point is 5.23 Ω. When the thermometer is inserted into a hot bath, the resistance of the platinum wire is 5.795 Ω. Calculate the temperature of the bath. (NCERT)
Answer:
Ro = 5 Ω, R100 = 5.23 Ω, Rt = 5.795 Ω
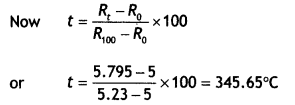
Question 25.
A battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1 Ω. Determine the equivalent resistance of the network and the current along each edge of the cube. (NCERT)
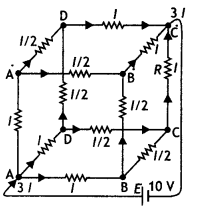
Answer:
The distribution of current is as shown.
Next take a closed-loop, say, ABCC’EA and apply Kirchhoff’s second rule:
lR – (1/2)lR – lR + E = 0
where R is the resistance of each edge and E is the emf of the battery.
Thus E = 5lR/2
Now if R<sub>eq</sub> is the equivalent resistance, then
R = E/31 = 5lR/6l = 5/6 R
Now current in the circuit is 3l × 5/6 R = 10 or l = 4 A.
Hence the other currents can also be found.
Question 26.
Determine the current in each branch of the network shown. (NCERT)
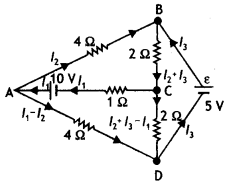
Answer:
Each branch of the network is assigned an unknown current to be determined by the application of Kirchhoff’s rules. To reduce the number of unknowns at the outset, the first rule of Kirchhoff is used at every junction to assign the unknown current in each branch. We then have three unknowns l1, l2 and l3 which can be found by applying the second rule of Kirchhoff to three different closed loops.
Kirchhoff’s second rule for the closed loop ADCA gives,
10 – 4(l1 – l2) + 2(l2 + l3 – l1) – l1 = 0 …(1)
that is, 7 l1 – 6l2 – 2l3 = 10
For the closed loop ABCA, we get
10 – 4l2 – 2 (l2 + l3) – l1 = 0 …(2)
That is, l1 + 6l2 + 2l3 = 10
For the closed loop BCDEB, we get
5 – 2(l2 + l3) – 2(l2 + l3– l1) = 0 ….(3)
That is 2 l1 – 4l2 – 4l3 = – 5
Equations (1), (2) and (3) are three simultaneous equations in three unknowns. These can be solved by the usual method to give
l1 = 2.5 A, l2 = 5/8 A, l3 = 15/8 A
The currents in the various branches of the network are
AB = 5/8 A, CA = 5/2 A, DEB = 15/8 A, AD = 15/8 A, CD = 0 A, BC = 5/2 A
Question 27.
In a metre bridge, the null point is found at a distance of 33.7 cm from A. If now resistance of 12 Ω is connected in parallel with 5, the null point occurs at 51.9 cm. Determine the values of R and S. (NCERT)
Answer:
From the first balance point we get
\(\frac{R}{S}=\frac{33.7}{66.3}\)
After S is connected in parallel with a resistance of 12 Ω, the resistance across the gap changes from S to Seq where and hence the new balance condition now gives
\(\frac{R}{S_{e q}}=\frac{51.9}{48.1}=\frac{R(S+12)}{12 S}\)
Substituting for R/S we have
\(\frac{51.9}{48.1}=\frac{(5+12)}{12} \times \frac{33.7}{66.3}\)
which gives S = 13.5 Ω and R = 6.86 Ω
Question 28.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm, what is the emf of the second cell? (NCERT)
Answer:
Given ε1 = 1.25 V, L1 = 35.0 cm and L2 = 63.0 cm, ε2 = ?
ε2 = \(\frac{L_{2} \times \varepsilon_{1}}{L_{1}}=\frac{1.25 \times 63.0}{35.0}\) = 2.25 V
Question 29.
The figure below shows a potentiometer circuit for the comparison of two resistances. The balance point with a standard resistor R = 10.0 Ω is found to be 58.3 cm, while that with the unknown resistance X is 68.5 cm. Determine the value of X. What might you do if you failed to find a balance point with the given cell of emf ε? (NCERT)
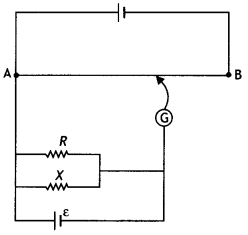
Answer:
Given R= 10.0 Ω, L1 = 58.3 cm, L2 = 68.5 cm, X = 1
Let k be the potential gradient along the wire AB, then
\(\frac{X}{R}=\frac{k L_{2}}{k L_{1}}\)
or
X = \(\frac{R \times L_{2}}{L_{1}}=\frac{10 \times 68.5}{58.3}\)
or
X= 11.75 Ω
If we fail to find a balance point with the given cell of emf e, it means the potential drop across R or X is greater than the potential drop across the potentiometer wire AB. Therefore to obtain the balance point on the wire, reduce the current in the circuit by putting a resistor in series with the circuit.
Question 30.
The figure below shows a 2.0 V potentiometer used for the determination of the internal resistance of a 1.5 V cell. The balance point of the cell in the open circuit is 76.3 cm. When a resistor of 9.5 Q is used in the external circuit of the cell, the balance point shifts to 64.8 cm length of the potentiometer wire. Determine the internal resistance of the cell. (NCERT)
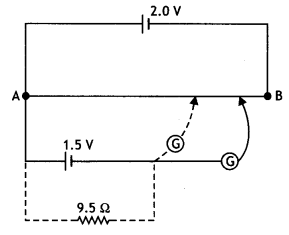
Answer:
Given 4 = 76.3 cm, ε = 1.5 V, R = 9.5 Ω, L2 = 64.8 cm
Internal resistance of a cell is given by the expression
r = \(\frac{\left(L_{1}-L_{2}\right) R}{L_{2}}\)
or
r = \(\frac{(76.3-64.8) \times 9.5}{64.8}\)
= 1.7 Ω