
On this page, you will find Circles Class 10 Notes Maths Chapter 10 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 10 Circles will seemingly help them to revise the important concepts in less time.
CBSE Class 10 Maths Chapter 10 Notes Circles
Circles Class 10 Notes Understanding the Lesson
1. Circle: A circle is a collection of all points in a plane which are at a constant distance from a fixed point. Here
Fixed point is called centre of the circle. Constant distance is called radius of the circle.
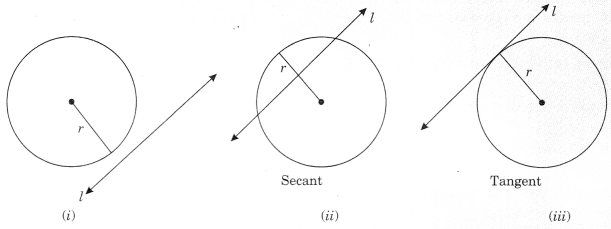
2. Considering a circle with centre ‘O’ and radius V and a line T in a plane.
Three different situations are there:
- When there is no common point between the circle and the line. Then the line is known as a non¬intersecting line
- When the line passes the circle in two points, the line is called a secant
- When a line meets the circle at a point, the line is called a tangent
The point at which the tangent touches the circle is called point of contact.
Facts related to tangent of circle.
Given: A circle with centre 0 and radius r.
A tangent XY at point P to the circle.
To prove: OP ⊥ XY
Construction: Take a point Q on XY other than P. Join OQ.
Proof: Point Q lies outside the circle.
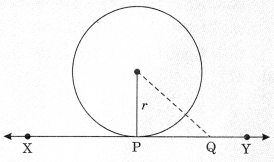
If point Q lies inside the circle then XY will become a secant and not a tangent to the circle.
∴ OQ > OP
which is true for every point on the line XY except the point P.
⇒ OP is the shortest of all the distances of the point O to the points of XY.
OP ⊥ XY
[ ∵ Shortest length from the point outside the line to the line is perpendicular]
Remark: A line drawn through the end point of radius and perpendicular to it, is the tangent to the circle.
Theorem 10.2: The lengths of tangents drawn from an external point to a circle are equal.
Given: PT and PS are tangents from point P to circle with centre 0.
To prove: PT = PS
Construction: Join OP, OT and OS.
Proof: In ΔOTP and ΔOSP
OT = OS [Radii of same circle]
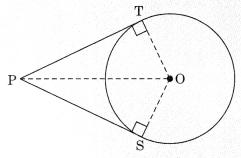
OP = QP
∠OTP = ∠OSP [Each 90º]
∴ ΔOTP ≅ ΔOSP [RHS]
⇒ PT = PS [CPCT]