CBSE Sample Papers for Class 9 Maths Set 1 with Solutions

Students can access the CBSE Sample Papers for Class 9 Maths with Solutions and marking scheme Set 1 will help students understand the difficulty level of the exam.

CBSE Sample Papers for Class 9 Maths Set 1 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

• This question paper contains 38 questions. All questions are compulsory.
• The question paper is divided into Five sections – Sections A, B, C, D, and E.
• In Section A, questions number 1 to 18 are multiple-choice questions (MCQs) and questions number 19 and 20 are Assertion-Reason based questions of 1 mark each.
• In Section B, questions number 21 to 25 are very short answer (VSA) type questions of 2 marks each.
• In Section C, questions number 26 to 31 are short answer (SA) type questions carrying 3 marks each.
• In Section D, questions number 32 to 35 are long answer (LA) type questions carrying 5 marks each.
• In Section E, questions number 36 to 38 are case-based integrated units of assessment questions carrying 4 marks each. Internal choice is provided in 2-mark questions in each case study.
• There is no overall choice. However, an internal choice has been provided in 2 questions in Section B, 2 questions in Section C, and 2 questions in Section D.
• Draw neat figures wherever required. Take π = \(\frac{22}{7}\) wherever required if not stated.
• The use of a calculator is not allowed.

Section-A

Consists of Multiple Choice Type questions of 1 mark each.

Question 1.
What is the common factor of x³ – x² and -22x² + 142x – 120?
(A) x
(B) x – 1
(C) x²
(D) 1
Answer:
(B) x – 1
Explanation:
-22x² + 142x – 120
= -22x² + 120x + 22x – 120
= -22x² + 22x + 120x – 120
= -22x(x – 1) + 120(x – 1)
= (x – 1)(-22x + 120)
x³ – x² = x² (x – 1)
∴ Common Factor = (x – 1).

Question 2.
Highways 20A and 56C run parallel to each other for 20 km in a state.
Which of the following statements is most likely to be true regarding them?
(A) Both highways are of the same length.
(B) There can be no link road between them.
(C) The highways make an angle 90° with each other.
(D) The distance between the two highways remains almost the same in the state.
Answer:
(D) The distance between the two highways remains almost the same in the state.
Explanation:
Parallel lines never intersect on being extended.

Question 3.
The equation of a line is ax + by + c = 0. What conditions ensure that the distance of the line from an axis is constant?
(A) c = 0 and a, b ≠ 0
(B) c < 0 and a, b ≠ 0
(C) c, b ≠ 0 and a = 1
(D) c, b ≠ 0 and a = 0
Answer:
(D) c, b ≠ 0 and a = 0
Explanation:
For distance of the line to be constant from an axis, a should be 0.

Question 4.
Atul likes to observe the stars with his telescope. He likes to track the movements of stars in the sky. He took a picture of the night sky one day. On that day, Mars was equidistant from Saturn and Jupiter.

He draws a circle such that the dots showing the planets Mars (M), Jupiter (J), Saturn (S) and a star Altair (A) lies on the boundary of a circle and ∠SMJ = 150°. What is the measure of ∠SAJ?
(A) 30°
(B) 45°
(C) 150°
(D) 210°
Answer:
(A) 30°
Explanation:
SMJA forms a quadrilateral,

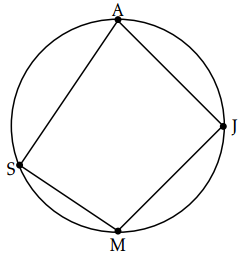
Opposite angles of a quadrilateral are supplementary.
∴ ∠SAJ + ∠SMJ = 180°
⇒ ∠SAJ + 150° = 180°
⇒ ∠SAJ = 30°

Question 5.
Histogram graphically represent the grouped frequency distribution with
(A) Upper limits of the classes
(B) Continuous classes
(C) Discontinuous classes
(D) Maximum frequency
Answer:
(B) Continuous classes

Question 6.
2√3 + √3 is equal to
(A) 2√6
(B) 6
(C) 3√3
(D) 4√6
Answer:
(C) 3√3
Explanation:
2√3 + √3 = 3√3

Question 7.
The linear equation 3x – 4y = 9 has
(A) a unique solution
(B) two solutions
(C) infinitely many solutions
(D) no solution
Answer:
(C) infinitely many solutions
Explanation:
Linear equations in two variables have infinitely many solutions.

Question 8.
The control room receives a message about trespassers located at (-9, -8). The trespassers were seen moving towards Road X on foot. The ranger immediately dispatches a team of guards in a jeep towards them. The guards encounter the trespassers before crossing Road X. Which of the following is most likely to be the location of the encounter?
(A) (-9, -14)
(B) (-9, -5)
(C) (-9, 4)
(D) (9, 5)
Answer:
(B) (-9, -5)
Explanation:
Since -5 is marked on x-axis, trespassers have to pass -5 to cross the load X. At this situation y-coordinate will remain the same. Thus, the correct location is (-9, -5).

Question 9.
Which will be the reflection of the points (-3, -2) in y-axis.
(A) (3, -2)
(B) (-3, 2)
(C) (3, 2)
(D) (2, 3)
Answer:
(A) (3, -2)
Explanation:
Point with coordinates (-3, -2) will lie in III quadrant
After reflection along y-axis they will moves to right side in IV quadrant,
∴ They will be (3, -2).

Question 10.
The equation x = 5, in two variables can be written as
(A) 1.x + 1.y = 5
(B) 1.x + 0.y = 5
(C) 0.x + 1.y = 5
(D) 0.x + 0.y = 5
Answer:
(B) 1.x + 0.y = 5
Explanation:
We have, x = 5
⇒ x – 5 = 0
⇒ 1.x + 0.y = 5

Question 11.
In the quadrilateral ABCD given below, ∠DAC = 90° and AB = AC = AD = DE = EB.

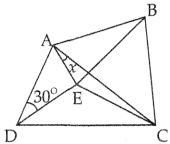
What is the value of ∠ABE?
(A) 20°
(B) 30°
(C) 45°
(D) 60°
Answer:
(B) 30°
Explanation:
In ΔABD
AD = AB (given)
∴ ∠ADB = ∠ABD (Angles opposite to equal sides are equal)
Thus ∠ABD = 30°
∴ ∠ABE = 30°

Question 12.
In an equilateral triangle ABC, D and E are the mid-points of sides AB and AC respectively, then length of DE is
(A) \(\frac{1}{2}\)BC
(B) \(\frac{1}{2}\)AB
(C) \(\frac{1}{2}\)AC
(D) \(\frac{2}{3}\)BC
Answer:
(A) \(\frac{1}{2}\)BC
Explanation:

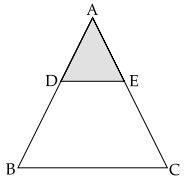
Since D and E are mid-points of sides AB and AC respectively. So, by mid-point theorem, DE = \(\frac{1}{2}\)BC.

Question 13.
ΔABC is an isosceles right-angled triangle in which ∠A = 90°. The value of ∠B is
(A) 65°
(B) 45°
(C) 90°
(D) 75°
Answer:
(B) 45°
Explanation:
AB = AC (given)
∴ ∠C = ∠B (Angle opposite to equal side)

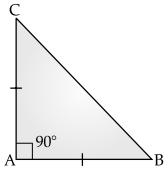
∠A + ∠B + ∠C = 180° [Angle Sum Property]
⇒ 90° + ∠B + ∠B = 180°
⇒ 2∠B = 90°
⇒ ∠B = 45°

Question 14.
Value of an angle which is five times its complement is
(A) 85°
(B) 55°
(C) 75°
(D) 65°
Answer:
(C) 75°
Explanation:
Let the angle be x.
Complement of x = (90° – x)
∴ x = 5(90° – x)
⇒ x = 450° – 5x
⇒ 6x = 450°
⇒ x = 75°

Question 15.
After rationalizing the denominator of \(\frac{7}{3 \sqrt{3}-2 \sqrt{2}}\), we get the denominator as
(A) 13
(B) 19
(C) 5
(D) 35
Answer:
(B) 19
Explanation:

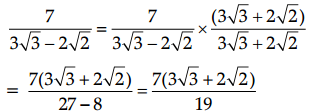
Therefore, we get the denominator as 19.

Question 16.
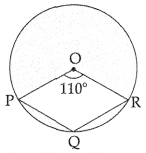
In the given figure, if ∠POR is 110°, then find the value of ∠PQR.

(A) 125°
(B) 135°
(C) 105°
(D) 115°
Answer:
(A) 125°
Explanation:
Reflex angle POR = 360° – 110° = 250°
∴ By degree measure theorem,
∠PQR = \(\frac{1}{2}\)(reflex angle POR)
= \(\frac{1}{2}\)(250°)
= 125°

Question 17.
A circle divides the plane, on which it lies, in ______ parts.
(A) 1
(B) 2
(C) 3
(D) 4
Answer:
(C) 3
Explanation:
3 parts (inside, outside and on the circle)

Question 18.
What will be the curved surface area of a hemisphere whose diameter is 14 cm?
(A) 308 cm²
(B) 544 cm²
(C) 208 cm²
(D) 754 cm²
Answer:
(A) 308 cm²
Explanation:
Given diameter of hemisphere = 14 cm
∴ radius of hemisphere = 7 cm
Thus, curved surface area = 2πr²
= 2 × \(\frac{22}{7}\) × 7 × 7
= 308 cm²

Directions: In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as:

(A) Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
(C) Assertion (A) is true, but Reason (R) is false.
(D) Assertion (A) is false, but Reason (R) is true.

Question 19.
Assertion (A): Three rational numbers between \(\frac{2}{5}\) and \(\frac{3}{5}\) are \(\frac{9}{20}\), \(\frac{10}{20}\) and \(\frac{11}{20}\).
Reason (R): A rational number between two rational numbers p and q is \(\frac{1}{2}\)(p + q).
Answer:
(B) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
Explanation:
In case of Assertion (A):
Multiplying and dividing \(\frac{2}{5}\) and \(\frac{3}{5}\) by 4, we get
\(\frac{2}{5} \times \frac{4}{4}=\frac{8}{20}\)
\(\frac{3}{5} \times \frac{4}{4}=\frac{12}{20}\)
Now, rational number are \(\frac{8}{20}\) and \(\frac{12}{20}\).
∴ \(\frac{9}{20}, \frac{10}{20}, \frac{11}{20}\) are three rational numbers between
\(\frac{2}{5}\) and \(\frac{3}{5}\).
∴ Assertion is true.
In case of Reason:
Now, rational number between two rational numbers = \(\frac{1}{2}\)(p + q), where p and q are rational numbers.
∴ Reason is true.
Therefore, Both A and R are true but R is not the correction explanation of A.

Question 20.
Assertion (A): x + 2y – \(\frac{2}{9}\) = 0 is a linear equation.
Reason (R): A linear equation in two variables is of the form ax + by + c = 0
Answer:
(A) Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct explanation of Assertion (A).
Explanation:
In case of Assertion (A):
x + 2y – \(\frac{2}{9}\) = 0
⇒ \(\frac{9 x+18 y-2}{9}\) = 0
⇒ 9x + 18y – 2 = 0
∴ Assertion is true.
In case of Reason (R):
A linear equation in two variables is of the form ax + by + c = 0 where a ≠ 0 and b ≠ 0.
Hence, Both (A) and (R) are true and (R) is the correct explanation of (A).

Section-B

Consists of 5 questions of 2 marks each.

Question 21.
Ravi planted a Red maple tree sapling. The height of the sapling is 0.25 m. The average growth rate of the height of a Red maple tree is 0.27 m per year. The average life of a Red maple tree is 80-100 years. Ravi estimated that his tree will grow up to 27 m. What is the likely reason behind his estimation?
Answer:
The average growth rate of a Red maple tree is 0.27 per year.
At this rate 100 year-old tree can reach the height of 0.27 × 100 = 27 m.

Question 22.
Find distances of points C(-3, -2) and D(5, 2) from X-axis and Y-axis.
Answer:
C(-3, -2)
Distance from X-axis = 2 units
Distance from Y-axis = 3 units
D(5, 2)
Distance from X-axis = 2 units
Distance from Y-axis = 5 units

Question 23.
The game of billiards is played with balls placed on a rectangular table. One ball is struck with the end of a stick, called a cue. The ball bounces into other balls and reflects off the sides of the table.

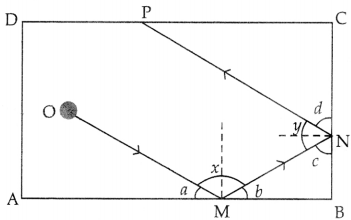
In a real game, the ball may spin, but for mathematical purposes, it is considered that the ball travels in a straight line with the same reflection and incidence angles. On a billiard table ABCD, the ball placed at O is struck with the cue. Why is the line OM parallel to PN?
Answer:

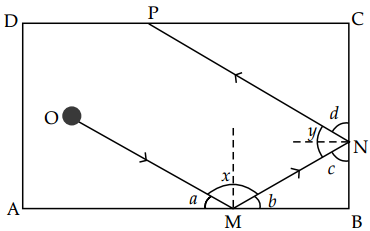
According to figure
Let angles on line AMB be a, x and b and angles on line BNC be c, y and d.
x = 180° – (a + b) ……(i)
y = 180° – (c + d) ………(ii)
Adding (i) and (ii), we get
x + y = 360° – (a + b + c + d)
= 360° – (2a + 2c) (∵ a = b and c = d)
= 360° – 2 × 90° (As, a + c = 90°)
= 180°
∴ x + y = 180°
Thus, lines OM and NP are parallel.
(∵ co-interior angles are supplementary)

Question 24.
Rita says, ‘For two triangles to be congruent, any three parameters of the six (3 sides and 3 angles) should be equal.’ Give examples in favour of and against her statement.
OR
‘Two triangles with a pair of equal angles are congruent.’ Why is it necessary to have the side between the two angles be of the same length for both triangles?
Answer:
According to Rita,
Criteria for congruency are SSS, ASA, SAS, AAS, RHS whereas SAA and AAA are not any criteria.
OR
As AAA is not any criteria for determining congruence of triangles.
Sides are necessary for valid congruency criteria which is ASA.
Hence, side between the two angles of same length is necessary for both triangles to be congruent.

Question 25.
Find the value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k.
OR
Find two different solutions of the equation 3x + y = 19.
Answer:
x = 2 and y = 1 is a solution of the equation 2x + 3y = k
⇒ 2 × 2 + 3 × 1 = k
⇒ k = 7
OR
3x + y = 19
⇒ y = 19 – 3x
When x = 1, y = 19 – 3x
= 19 – 3(1)
= 16
When x = 5
y = 19 – 3(5)
= 19 – 15
= 4
Hence, the two solutions are (1, 16) and (5, 4).

Section-C

Consists of 6 questions of 3 marks each.

Question 26.
A number line consists of an infinite number of points. Points on it are associated with a rational number.
Khushi says – ‘A point on the number line can represent different forms of a rational number.
Akash says – ‘I think each point represents a unique rational number.
Who is correct? Given an example to support your argument.
Answer:
Both Khushi and Akash are correct.
Khushi is correct as numbers including 1/2, 2/4, 3/6, 4/8 and 0.5 can be represented by the same point on the number line.
Akash is also correct as each point on the number line represents a unique real number.

Question 27.
The area of a triangle is equal to the area of a rectangle.
The area of the rectangle is equal to the area of a parallelogram.
What is the relation between the area of the triangle and the area of the parallelogram?
Answer:
Area of triangle = Area of a rectangle (given)
And, Area of rectangle = Area of a parallelogram (given)
According to Euclid’s Axiom,
Things which are equal to the same thing are equal to one another.
∴ Area of triangle = Area of parallelogram.

Question 28.
In the fig, given below, an exterior angle of a triangle is 130° and the two interior opposite angles are equal. Find each angle of the triangle.

OR
In given figure PO ⊥ AB, if x : y : z = 1 : 3 : 5, then find the degree measure of x, y and z.

Answer:

In a triangle ABC
x + x = 130° (exterior angle is equal to the sum of interior opposite angles)
⇒ 2x = 130°
⇒ x = 65°
∴ ∠A = ∠B = 65°
∠ACB + ∠ACD = 180° (Linear pair)
⇒ ∠ACB + 130° = 180°
⇒ ∠ACB = 50°
Hence, ∠ABC = 65°, ∠BAC = 65° and ∠ACB = 50°
OR
OP ⊥ AB
So, ∠POA = 90°
Let x =∠POQ = a
y = ∠QOR = 3a
z = ∠ROA = 5a
a + 3a + 5a = 90°
⇒ 9a = 90°
⇒ a = 10°
∴ x = 10°
∴ y = 3 × 10 = 30°
∴ z = 5 × 10 = 50°

Question 29.
Factorize: x³ – 3x² – 9x – 5.
OR
Factorize: 2y³ + y² – 2y – 1.
Answer:
Let p(x) = x³ – 3x² – 9x – 5
Since, p(-1) = -1 – 3 + 9 – 5 = 0
Therefore, (x + 1) is a factor of x³ – 3x² – 9x – 5.
∴ (x³ – 3x² – 9x – 5) = (x + 1)(x² – 4x – 5)
Now, x² – 4x – 5 = x² – 5x + x – 5
= x(x – 5) + 1(x – 5)
x² – 4x – 5 = (x + 1)(x – 5)
∴ p(x) = (x + 1)(x – 5)(x + 1)
OR
Let p(y) = 2y³ + y² – 2y – 1
∴ p(-1) = 2(-1)³ + (-1)² – 2(-1) – 1
= -2 + 1 + 2 – 1
= 0
∴ (y + 1) is a factor of given polynomial.
∴ 2y³ + y² – 2y – 1 = (y + 1)(2y² – y – 1)
Now, 2y² – y – 1 = 2y² – 2y + y – 1
= 2y(y – 1) + 1(y – 1)
= (2y + 1)(y – 1)
∴ p(y) = (y + 1)(2y + 1)(y – 1)

Question 30.
What is the area of a triangle with side lengths 20 cm, 20 cm and 8 cm?
Answer:
Let a, b, c be the given side,
So, a = 20 cm, b = 20 cm, c = 8 cm
Semi-perimeter of original triangle

Question 31.
Simplify (2d + 3b)³ – (2a – 3b)³.
Answer:
Let (2a + 3b)³ – (2a – 3b)³ = x³ – y³,
where 2a + 3b = x and 2a – 3b = y
∴ x³ – y³ = (x – y)(x² + xy + y²)
= [(2a + 3b) – (2a – 3b)][(2a + 3b)² + (2a + 3b)(2a – 3b) + (2a – 3b)²]
= 6b[(4a² + 12ab + 9b²) + (4a² – 9b²) + (4a² – 12ab + 9b²)]
= 6b(12a² + 9b²)
= 6b × 3 × (4a² + 3b²)
= 18b(4a² + 3b²)

Section-D

Consists of 4 questions of 5 marks each.

Question 32.
If f(x) = x² – 5x + 7, evaluate f(2) – f(-1) + f(\(\frac{1}{3}\))
OR
If f(x) = x⁴ – 4x³ + 3x² – 2x + 1, then check whether f(0) × f(-1) = f(2) is true or not.
Answer:
Given, f(x) = x² – 5x + 7
Then, f(2) = 2² – 5 × 2 + 7 = 1
and f(-1) = (-1)² – 5(-1) + 7 = 13
and \(f\left(\frac{1}{3}\right)=\left(\frac{1}{3}\right)^2-5\left(\frac{1}{3}\right)+7=\frac{49}{9}\)
Thus, f(2) – f(-1) + f(\(\frac{1}{3}\)) = 1 – 13 + \(\frac{49}{9}\) = \(\frac{-59}{9}\)
OR
Given, f(x) = x⁴ – 4x³ + 3x² – 2x + 1
f(0) = 1
and f(-1) = (-1)⁴ – 4(-1)³ + 3(-1)² – 2(-1) + 1
= 1 + 4 + 3 + 2 + 1
= 11
and f(2) = (2)⁴ – 4(2)³ + 3(2)² – 2(2) + 1
= 16 – 32 + 12 – 4 + 1
= 29 – 36
= -7
∴ f(0) × f(-1) = 11 ……(i)
f(2) = -7 …..(ii)
11 ≠ -7
∴ f(0) × f(-1) ≠ f(2) (Not true)

Question 33.
The blood groups of 30 students of class IX are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
(i) Represent this data in the form of a frequency distribution table.
(ii) Which is the most common and which is the rarest blood group among these students?
Answer:
(i) Frequency Distribution Table:

(ii) Blood group ‘O’ is most common as it has highest frequency i.e., 12.
Blood group AB is rarest as its frequency is 3.

Question 34.
In the given figure ∠SPQ = 45°, ∠POT = 150° and O is the centre of circle. Find the measures of ∠RQT, ∠RTQ and ∠PUT.

OR
In the given figure, AB and CD are two parallel chords of a circle with centre O and radius 5 cm such that AB – 8 cm and CD = 6 cm. If OP is perpendicular to AB and OQ is perpendicular to CD, determine the length of PQ.

Answer:
In the given figure
∠POT + reflex ∠POT = 360°
150° + reflex ∠POT = 360°
reflex ∠POT = 210°
reflex ∠POT = 2∠PST
(Angle subtended by arc at the centre is twice at circumference)
210° = 2∠PST
∴ ∠PST = 105°
∠PQT + ∠PST = 180°
(Opposite angles of cyclic quadrilateral PQTS are supplementary)
∠PQT = 180° – 105° = 75°
∠RQT + ∠PQT = 180° (Linear pair)
∠RQT = 180° – 75° = 105°
∠RTQ = ∠SPQ = 45°
(Exterior angle of a cyclic quadrilateral is equal to interior opposite angle)
∠PUT= \(\frac{1}{2}\)∠POT
(Angle subtended by an arc at the centre is twice the angle at the remaining circle)
= \(\frac{1}{2}\) × 150°
= \(\frac{1}{2}\) × 150°
∴ ∠PUT = 75°

OR
Construction: Join OA and OC.
Proof: Since perpendicular from centre of the circle to the chord bisects the chord.

∴ AP = PB = \(\frac{1}{2}\)AB = 4 cm
and, CQ = QD = \(\frac{1}{2}\)CD = 3 cm
In ∆OAP,
OP² = OA² – AP² (Pythagoras theorem)
OP² = 5² – 4²
= 25 – 16
= 9
∴ OP = 3 cm
In ∆OCQ,
OQ² = OC² – CQ² (Pythagoras theorem)
= 5² – 3²
= 25 – 9
= 16
∴ OQ = 4 cm
∴ PQ = OP + OQ = 3 + 4 = 7 cm

Question 35.
A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 5 cm. Find the volume of the solid so obtained. If, it is revolved about the side 12 cm, what would be the ratio of volumes of two solids obtained in two cases?
Answer:
Case I: When revolved about the side 5 cm.
Here, r = 12 cm, h = 5 cm
Volume = \(\frac{1}{3} \pi r^2 h\)
= \(\frac{1}{3} \pi \times(12)^2 \times 5\)
= 240π cm³

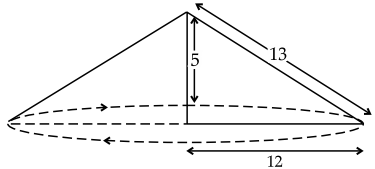
Case II: When revolved about 12 cm, r = 5 cm, h = 12 cm

∴ Volume = \(\frac{1}{3} \pi r^2 h\)
= \(\frac{1}{3}\) × 5 × 5 × 12π
= 100π cm³
∴ Ratio of the two-volume = 240π : 100π = 12 : 5

Section-E

Cased-Based Subjective Questions.

Question 36.
Read the following passage and answer any four questions.
Democracy has given people a powerful right to VOTE. In India, every citizen over 18 years of age has the right to vote. Instead of enjoying it as a holiday, one must vote if he/she truly wants to contribute to the nation-building process and bring about a change.

A survey was done in a small area in which \(\sqrt{9+2 x}-\sqrt{2 x}\) voters were men and \(\frac{5}{\sqrt{9+2 x}}\) voters were women.
(i) Find x, if number of men is equal to number of women.
(ii) Find value of \(\frac{7^{\frac{1}{5}}}{7^{\frac{1}{3}}}=1\).
OR
If r is rational and s is irrational, then what will be the result of their sum, difference, multiplication and division.
(iii) Which mathematical concept is used here?
Answer:
(i) \(\sqrt{9+2 x}-\sqrt{2 x}\) = \(\frac{5}{\sqrt{9+2 x}}\)
⇒ \(\sqrt{9+2 x}[\sqrt{9+2 x}-\sqrt{2 x}]\) = 5
⇒ \((\sqrt{9+2 x})^2-\sqrt{2 x(9+2 x)}\) = 5
⇒ 9 + 2x – 5 = \(\sqrt{2 x(9+2 x)}\)
⇒ 4 + 2x = \(\sqrt{2 x(9+2 x)}\)
Squaring both sides,
⇒ (4 + 2x)² = \((\sqrt{2 x(9+2 x)})^2\)
⇒ 16 + 4x² + 16x = 18x + 4x²
⇒ 16 = 2x
⇒ x = 8
OR
If r is rational and s is irrational, then their sum, difference, product and division will be irrational.
(ii) \(\frac{7^{\frac{1}{5}}}{7^{\frac{1}{3}}}=7^{\frac{1}{5}-\frac{1}{3}}=7^{\frac{3-5}{15}}=7^{\frac{-2}{15}}\)
(iii) Mathematical concept used here is Number system.

Question 37.
Given below is the map giving the position of four housing societies in a township connected by a circular road A.

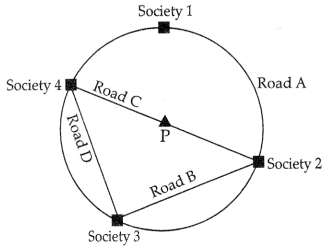
Society 2 and 3 are connected by straight Road B, Society 4 and 2 are connected by straight Road C and Society 4 and 3 are connected by Road D. Point P denotes the position of a park. The park is equidistant to all four societies. Rubina claims that it is not possible to construct another circular road connecting all four societies. Two new roads, Road E and Road F were constructed between Society 4 and 1 and Society 1 and 2.

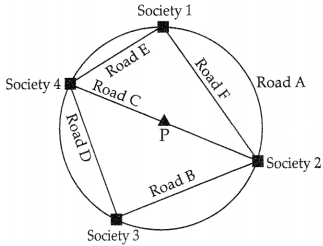
(i) What is the position of the park P with respect to Road A?
(ii) What would be the measure of the sum of angles formed by the straight roads at society 1 and society 3?
OR
Priya said, “Minor arc corresponding to Road B is congruent to minor arc corresponding to Road D.” Do you agree with Priya? Give reason to support your, answer.
(iii) Alex says, “The angle made by road B on road D is a right angle.”
Jai and Angad give different justifications to support Alex’s claim.
Jai says, “Angles in the same segment of a circle are equal.”
Angad says, “The angle in a semicircle is a right angle.”
Who has given the correct justification?
Answer:
(i) Since, Road A is circular road, therefore park P is centre of Road A.
As Society 1, Society 2, Society 3 and Society 4 from a cyclic quadrilateral.
∴ Sum of angles formed by straight road at Society 1 and Society 2 = 180°. (Opposite angles of cyclic quadrilateral)
OR
Yes, Priya is correct.
As, arc corresponding to two equal roads (chords) are congruent.
(iii) Angad is right because Road B and Road D make an angle in a semicircle.

Question 38.
Glass buildings can be strengthened using iron frames. A glass structure and its iron frame are shown below.

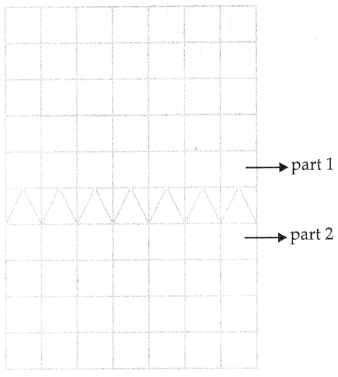
The frame consists of equal triangles. The dimensions of a triangle are shown below.

(i) How much area is enclosed by one triangle?
(ii) What is the area of part 1 of the frame?
OR
Is the area of part 1 equal to the area of part 2? Why?
(iii) Maintenance of the building’s exterior is done by a company. The company charges ₹ 750 per square meter per month. What will be the monthly maintenance charges?
Answer:
(i) Let a, b, c are sides of the triangle.
Here, a = 8 m, b = 6 m, c = 10 m

(ii) Number of triangles in one frame = 4
Number of triangles in Part 1 = 154
∴ Area of part 1 = 154 × 24 = 3696 m²
OR
No, Area of part 1 is not equal to area of part 2.
As, Number of triangles in part 2 = 126
∴ Area of part 2 = 126 × 24 = 3024 m²
And Area of part 1 = 3696 m² (from above)
(iii) Maintenance charges per square metre per month = ₹ 750
Total area of frame = (3696 + 3024) m² = 6720 m²
Monthly maintenance charges = 6720 × ₹ 750 = ₹ 50,40,00