CBSE Sample Papers for Class 12 Physics Set 4 with Solutions

Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Physics Set 4 with Solutions

Time : 3 Hours
Maximum Marks: 70

General Instructions :

1. There are 33 questions in all. All questions are compulsory.
2. This question paper has five sections: Section A, Section B, Section C. Section D and Section E.
3. Air the sections are compulsory.
4. Section A contains sixteen questions, twelve MCQ and four Assertion-Reasoning based questions of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study-based questions of four marks each and Section E contains three long answer questions of five marks each.
5. There is no overall choice. However, an internal choice has been provided in one question in Section B, one question in Section C, one question in each CBQ in Section D and all three questions in Section E. You have to attempt only one of the choices in such questions.
6. Use of calculators is not allowed.
7. You may use the following values of physical constants wherever necessary
   (i) c = 3 ×10⁸ m/s
   (ii) m_e = 9.1 × 10^-31 kg
   (iii) e = 1.6 × 10^-19 C 
   (iv) μ₀= 4π × 10^-17 TmA^-1
   (v) h = 6.63 × 10^-34 Js  
   (vi) ε₀ = 8.854 ×10^-12 C²N^-1m^-2
   (vii) Avogadro’s number = 6.023 × 10²³ per gram mole

Section – A

The following questions are multiple-choice questions with one correct answer. Each question carries 1 mark. There is no internal choice in this section.

Question 1.
The total flux through the faces of the cube with side of length a if a charge 2q is placed at corner A of the cube is:

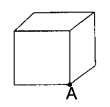
(a) \(\frac{q}{8 \varepsilon_0}\)

(b) \(\frac{q}{2 \varepsilon_0}\)

(c) \(\frac{q}{4 \varepsilon_0}\)

(d) \(\frac{2 q}{\varepsilon_0}\)
Answer:
(c) \(\frac{q}{4 \varepsilon_0}\)

Explanation: In the figure, when a charge 2q is placed at comer A of the cube, it is being shared equally by eight cubes. So, total flux through the faces of the given cube = \(\frac{q}{4 \varepsilon_0}\)

Question 2.
In the given figure, a charge Q is fixed. Another charge q is moved along circular arc MN of radius r around it, from the point M to the point N such that the length of the arc MN = l. The work done in this process is :

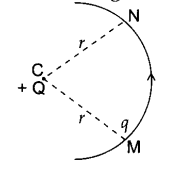
(a) zero

(b) \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{\mathrm{Q} q}{r^2} l\)

(c) \(\frac{\mathrm{Qq}}{2 \varepsilon_0 r^2} l\)

(d) \(\frac{\mathrm{Q} q}{2 \pi \varepsilon_0 r^2}\)
Answer:
(a) zero

Explanation: As distance of point M and N from C is constant so They are at same potential.
\(\mathrm{V}_{\mathrm{M}}=\mathrm{V}_{\mathrm{N}}=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r}\)

V_M-V_N =0

The work done in this process W = (V_M-V_N)q = 0

Question 3.
A potential difference V is applied to a copper wire. If the potential difference is increased to 2V, then the drift velocity of electrons will:
(a) be double the initial velocity
(b) remain same
(c) be √2 times the initial velocity
(d) be half the initial velocity
Answer:.

(a) be double the initial velocity

Explanation: As we know that,
I = nev_d

I ∝ v_d
From Ohm’s law,

V ∝ I ∝ v_d
If the potential difference is doubled, drift velocity of electrons will also double.

Question 4.
Magnetic field due to a ring having n turns at a distance x on its axis is proportional to (if r = radius of ring):
(a) \(\frac{r}{\left(x^2+r^2\right)}\)

(b) \(\frac{n r^2}{\left(x^2+r^2\right)^{3 / 2}}\)

(c) \(\frac{r^2}{\left(x^2+r^2\right)^{3 / 2}}\)

(d) \(\frac{n^2 r^2}{\left(x^2+r^2\right)^{3 / 2}}\)
Answer:
(b) \(\frac{n r^2}{\left(x^2+r^2\right)^{3 / 2}}\)

Explanation: Magnetic field on the axis of circular coil carrying current,

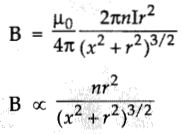
Question 5.
A current of 10 A is passing through a long wire which has semicircular loop of the radius 20 cm as shown in the figure. Magnetic field produced at the centre of the loop is:

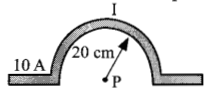
(a) 4πμT

(b) 2πμT

(c) 10πμT

(d) 5πμT
Answer:
(d) 5πμT

Question 6.
A north pole of strength 50 Am and south pole of strength 100 Am are separated by a distance of 10 cm in air.
Find the force between them:
(a) 20 × 10^-6 N
(b) 25 × I0^-3 N
(c) 30 × 10^-18 N
(d) 50 × 10^-3 N
Answer:
(d) 50 × 10^-3 N

Explanation: Force between magnetic poles in air is given by,

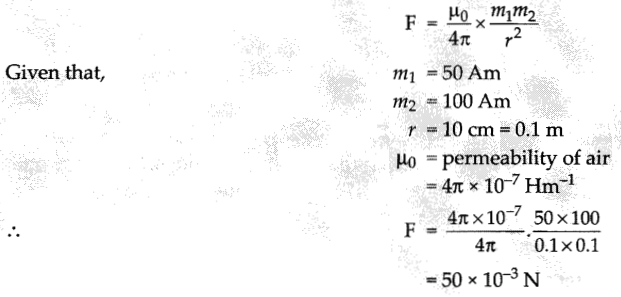
Question 7.
An air core solenoid has 1000 turns and is one metre long. It cross-sectional area is 10 cm². Its self-inductance is:
(a) 0.1256 mH
(b) 1.256 mH
(c) 12.56 mH
(d) 125.6 mH
Answer:
(b) 1.256 mH

Explanation: Self-inductance of solenoid coil having N number of tupns, length l and area of cross-section A is given by,

\(\mathrm{L}=\mu_0 \frac{\mathrm{N}^2}{l} \mathrm{~A}\)

Here, N = 1000,
A = 10 cm²,
or A = 10 × 10^-4 m²
and l = 1 m
Substituting these values in the above equation, we get

\(\mathrm{L}=4 \pi \times 10^{-7} \times \frac{(1000)^2}{1} \times 10 \times 10^{-4}\)

L = 1.256 mH

Question 8.
The selectivity of a series LCR a.c. circuit in large, when:
(a) L is large, R is large
(b) L is small and R is small
(c) L is large and R is small
(d) L = R
Answer:
(c) L is large and R is small

Explanation: Since, selectivity depends on the quality of resonance. The quality factor is given by Q = ω₀L/R. High value of quality factor make sure that the resonance curve is sharp, sharper the resonance curve, more selective is the LCR circuit.

Question 9.
If v = \(\frac{1}{\sqrt{\mu \varepsilon}}\) gives the speed of an electromagnetic wave in a material medium, μ the permeability of the medium and ε its permittivity. What is its effect on frequency?
(a) Frequency increases gradually
(b) Frequency decreases
(c) Frequency first increases and then decreases to zero
(d) Frequency remain unchanged
Answer:
(d) Frequency remain unchanged

Explanation: The frequency of an electromagnetic wave is independent of the medium in which the wave travels.

Question 10.
A short pulse of white light is incident from air to a glass slab at normal incidence. After travelling through the slab, the first colour to emerge is :
(a) blue
(b) green
(c) violet
(d) red
Answer:
(d) red

Explanation: Since v ∝ λ, the light of red colour is of highest wavelength and therefore of highest speed. Therefore, after travelling through the slab, the red colour emerge first.

Question 11.
A single diode can be used :
(a) only as full wave rectifier
(b) only as half wave rectifier
(c) both half wave and full wave rectifier
(d) neither half wave nor full wave rectifier
Answer:
(b) only as half wave rectifier

Explanation: A diode is a p-n junction which acts as open switch in reverse biasing and closed switch in forward biasing. A diode can be used for rectification i.e. to Convert A.C. voltage into D.C. voltage. There are two type of rectifying circuit-full wave rectifier and half wave rectifier. But a single diode works as a half wave rectifier.

Question 12.
Bohr’s atom model assumes :
(a) mass of electron remains constant
(b) electrons in a quantized orbit will not radiate energy
(c) the nucleus is of infinite mass and is at in rest
(d) all the above conditions
Answer:
(d) all the above conditions

Explanation: In 1913, Niels Bohr’s proposed a model for the hydrogen atom. The Bohr’s model was based on the following assumptions:
(1) The electron in a hydrogen atom travels around the nucleus in a circular orbit.
(2) The nucleus is of infinite mass and is in rest.
(3) Electrons in a quantized orbit will not radiate energy.
(4) Mass of electron remains constant.

(Direction: Question 16 to 18) Two statements are given-one labelled Assertion (A) and the other labelled
Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below:
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true and R is not the correct explanation of A.
(c) A is true, but R is false.
(d) A is false, and R is also false.

Question 13.
Assertion: Critical angle is minimum for red colour.
Reason : Because critical angle

\(\theta_c=\sin ^{-1}\left(\frac{1}{2 \mu}\right) \text { and } \mu \propto \frac{1}{\lambda} \text {. }\)

Answer:
(d) A is false, and R is also false.

Explanation: Critical angle is minimum for violet colour, critical angle = 0C = sin-1 \(\)

Question 14.
Assertion : The de-Broglie wavelength equation has significance for any microscopic and sub microscopic particles.
Reason : de-Broglie wavelength is inversely proportional to the mass of the object its velocity is constant.
Answer:
(a) Both A and R are true and R is the correct explanation of A.

Explanation: As de-Broglie wavelength
\(\lambda=\frac{h}{m v}\)

so, for constant velocity,

\(\lambda \propto \frac{1}{m}\)

Lesser the mass greater will be its de-Broglie wavelength.

Question 15.
Assertion: The value of current through p-n junction in the given figure will be 10 mA.

Reason: In the above figure, p-side is at higher potential than n side.
Answer:
(b) Both A and R are true, but R is not the correct explanation of A.
Explanation: As we know that,
V =5-2=3 V

\(I=\frac{V}{R}=\frac{3}{300}=\frac{1}{100} A\)
= 10 mA

Question 16.
Assertion : When two coils are wound on each other, the mutual induction between the coils is maximum.
Reason: Mutual induction does not depend on the orientation of the coils.
Answer:
(a) Assertion is true, but reason is false.
Explanation: The manner in which the two coils are oriented, determines the coefficient of coupling between them.

\(\mathrm{M}=\mathrm{K} \cdot \sqrt{\mathrm{L}_1 \mathrm{~L}_2}\)
When the two coils are wound on each other, the coefficient of coupling is maximum and hence mutual inductance between the coil is maximum.

Section – B

Question 17.
Name the constituent radiation of electromagnetic spectrum which
(i) is used in ovens for cooking purposes.
(ii) is used in scientific research.
(iii) is used in treatments of cancer and tumours.
Answer:
(i) Microwaves
(ii) X-rays
(iii) Gamma rays

Question 18.
Draw magnetic field lines when a (i) diamagnetic, (ii) paramagnetic substance is placed in an external magnetic field. Which magnetic property distinguishes this behaviour of the field lines due to the two substances ?
Answer:
Figure 1 shows magnetic field lines when (i) diamagnetic materials are placed in external magnetic field.

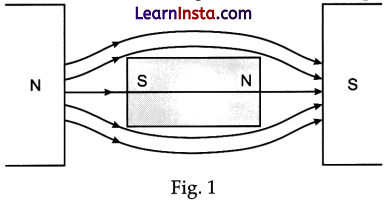
Figure 2 shows magnetic field lines, when (ii) paramagnetic materials are placed in external magnetic field.

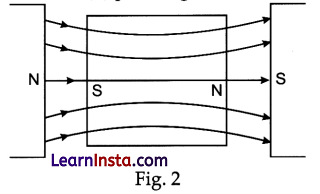
Magnetic dipole moment of materials are responsible for this diamagnetic material has zero magnetic moment. Paramagnetic material has non-zero magnetic moment.

Question 19.
State two points of difference between the interference pattern obtained in Young’s double slit experiment and the diffraction pattern due to a single slit.
Answer:
The two differences between the interference patterns obtained in Young’s double slit experiment and the diffraction pattern due to a single slit are as follows:
(i) The fringes in the interference pattern obtained from diffraction are of varying width, while in case of interference, all are of the same width.
(ii) The bright fringes in the interference pattern obtained from diffraction have a central maximum followed by fringes of decreasing intensity, whereas in case of interference, all the bright fringes are of equal width.

Question 20.
Draw the intensity pattern for single slit diffraction and double slit interference.
Answer:
Intensity pattern for single slit diffraction :

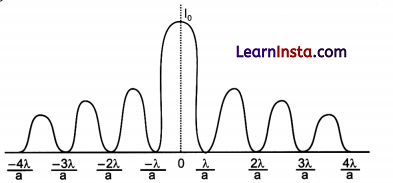
Intensity pattern for double slit interference :

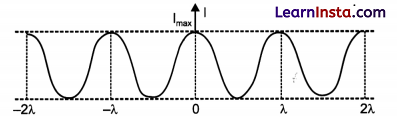
Question 21.
Draw circuit diagrams to illustrate forward biasing and reverse biasing of a diode?
OR
Briefly explain how a potential barrier is set up across a p-n junction as a result of diffusion and drift of the charge carriers.
Answer:
Forward biasing of a diode: In this arrangement, the positive terminal of battery is connected to p-end and negative terminal to n-end of the crystal, so that an external electric field E is established directed from p to w-end to oppose the internal field E_i. Thus, the junction is said to be conducting.

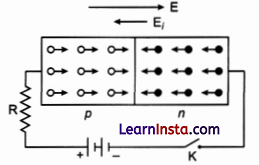
Reverse biasing of a diode: In this arrangement the positive terminal of battery is connected to n-end and negative to p-end of the crystal, so that the external field is established to support the internal field E_i.

OR
Potential Barrier:

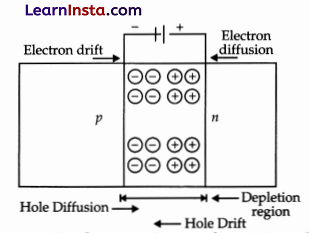
The accumulation of negative charges in the p-region and positive charges in the n-region set up a potential difference across the junction. This acts as a barrier and is called potential barrier.

Section – C

Question 22.
State the principle of an ac generator and explain its working with the help of a labelled diagram. Obtain the expression for the emf induced in a coil having N turns each of cross-sectional area A, rotating with a constant angular speed ‘ω’ in a magnetic field, directed perpendicular to the axis of rotation.
OR
Draw a labelled diagram of a step-up transformer. Obtain the ratio of secondary to primary voltage in terms of number of turns and currents in the two coils.
Answer:
Principle of AC generator: The AC generator is based on the principle of electromagnetic induction. When closed coil is rotated in a uniform field with its axis perpendicular to field, then magnetic flux changes and emf is induced.
Working: When the armature coil rotates, the magnetic flux linked with it changes and produces induced current. If initially, coil PQRS is in vertical position and rotated clockwise, then PQ moves down and SR moves up. By Fleming’s right hand rule, induced current flows from Q to P and S to R which is the first half rotation of coil. Brush B₁ is positive terminal and B₂ is negative. In second half rotation, PQ moves up and SR moves down. So induced current reverses and the alternating current is produced in this manner by the generator.

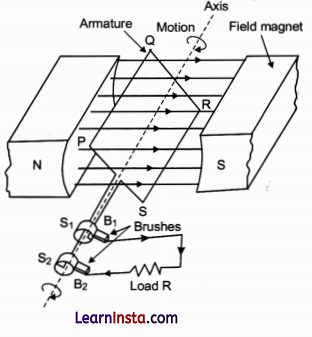
Expression for emf induced: If number of turns in coil = N, cross-section = A, angular speed of rotation = ω, magnetic field = \(\overrightarrow{\mathrm{B}}\), then to find emf induced,
Flux through the coil when its normal makes angle θ with the field,
Φ = BA cos θ
When coil rotates with angular velocity co and turns through 0 in time f then 0 = cof
Φ = BA cos ωt
When coil rotates, Φ changes to set an induced emf.

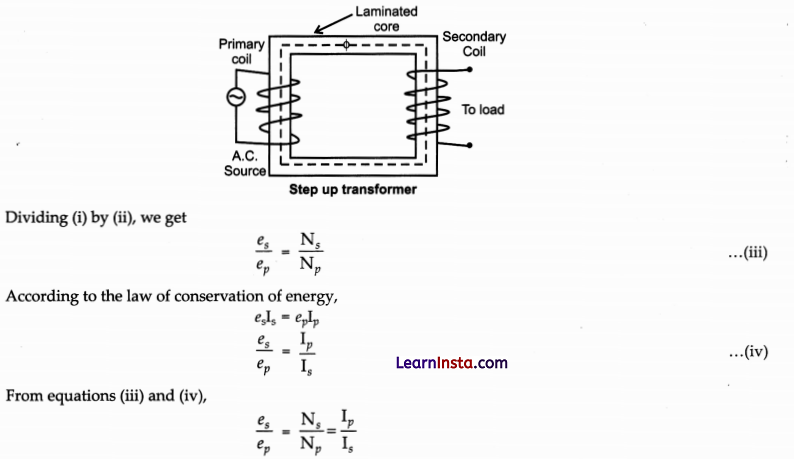
Question 23.
Two long coaxial insulated solenoids, S₁ and S₂ of equal lengths are wound one over the other as shown in the figure. A steady current ‘I’ flow through the inner solenoid S₁ to the other end B, which is connected to the outer solenoid S₂ through which the same current I flows in the opposite direction so as to come out at end A. If n₁ and n₂ are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point (i) inside on the axis and (ii) outside the combined system.

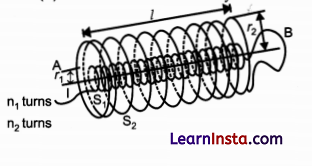
Answer:
(i) The magnetic field due to a current carrying solenoid :

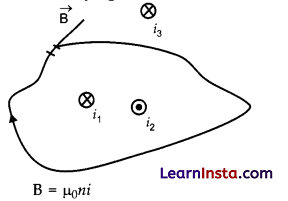
where, n = number of turns per unit length, i = current through the solenoid.
Now, the magnetic field due to solenoid S₁ will be in the upward direction and the magnetic field due to S₂ will be in the downward direction (by right-hand screw rule).

B_net = B₁ – B₂

B_net = μ₀n₁I- μ₀n₂I

= μ₀I (n₁– n₂)
(ii) The magnetic field is zero outside a solenoid.

Question 24.
(i) Write the expression for the magnetic force acting on a charged particle moving with velocity v in the presence of magnetic field B.

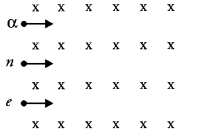
(ii) A neutron, an electron and an alpha particle moving with equal velocities, enter a uniform magnetic field going into the plane of the paper as shown. Trace their paths in the field and justify your answer.
Answer:
(i) A charge particle having charge q is moving with velocity ‘v’ in a magnetic field of field strength ‘B’ then the force acting on it is given by the formula F = q \((\vec{v} \times \overrightarrow{\mathrm{B}})\) and F = qv B sin θ (where 0 is the angle between velocity vector of magnetic field).
Direction of force is given by the cross product of velocity and magnetic field.
(ii) a-particle will trace circular path in anticlockwise direction as it’s deviation will be in the direction of \((\vec{v} \times \overrightarrow{\mathrm{B}})\).
Neutron will pass without any deviation as magnetic field does not exert force on neutral particle.

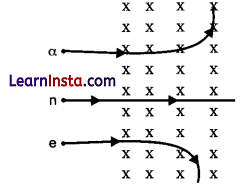
Electron will trace circular path in clockwise direction as its deviation will be in the direction opposite to \((\vec{v} \times \overrightarrow{\mathrm{B}})\) with a smaller radius due to large charge/mass ratio as \(r=\frac{m v}{q \mathrm{~B}}\).

Question 25.
(i) In the following diagram, is the junction diode forward biased or reverse biased?

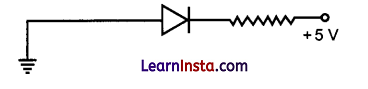
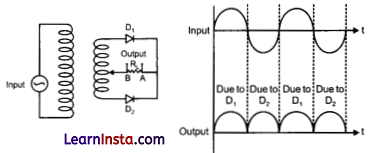
(ii) Draw the circuit diagram of a full wave rectifier and state how it works.
Answer:
(i) Reverse biased.
(ii) Full wave Rectifier :
Diode conducts only when the junction is forward biased. Hence, during first half cycle of input A.C., D₁ will conduct while D₂ will not and current in R_L will flow from A to B. During second half cycle of input A.C., diode D₂ will conduct while D₁ will not conduct and current will again flow from A to B in R_L. Hence, complete cycle will become unidirectional.

Question 26.
Calculate for how many years will the fusion of 2.0 kg deuterium keep 800 W electric lamp glowing. Take the fusion reaction as :

Answer:

Question 27.
Given a uniform electric field \(\overrightarrow{\mathrm{E}}=2 \times 10^3 \hat{i} \mathrm{~N} / \mathrm{C}\). Find the flux of this field through a square Gf side 20 cm, whose plane is parallel to the Y-Z plane. What would be the flux through the same square, if the plane makes an angle of 30° with the X-axis ?
Answer:
When the plane is parallel to the Y-Z plane

\(\phi=\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{A}}\)

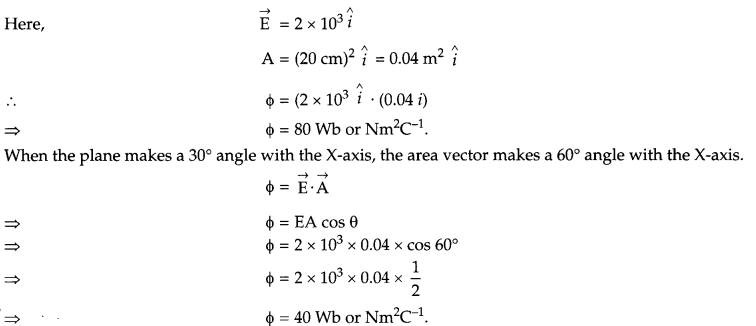
Question 28.
Figure shows the stopping potential (V₀) for the photoelectron versus (1/λ.) graph, for two metals A and B, λ being the wavelength of incident light.

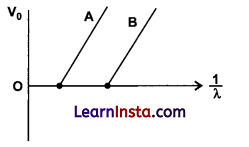
(i) How is the value of Planck’s constant determined from the graph?
(ii) If the distance between the light source and the surface of metal A is increased, how will the stopping potential for the electrons emitted from it be effected? Justify your answer.
OR
Light of same wavelength is incident on three photo-sensitive surfaces A, B and C. The following observations are recorded.
(i) From surface A, photo electrons are not emitted.
(ii) From surface B, photo electrons are just emitted.
(iii) From surface C, photo electrons with some kinetic energy are emitted.
Compare the threshold frequencies of the three surfaces and justify your answer.
Answer:
(i) We know that

Planck’s constant can easily be determined by substituting the values of the slope of graph, speed of light and electronic charge in equation (ii).
(ii) Stopping potential only depends on frequency of incident light. If the distance is increased, intensity will decrease but no change takes place in stopping potential.

OR
From the observations made (surface A, B and C) on the basis of photoelectric effect:
(i) For surface A, threshold frequency is more than frequency of incident light, so no emission occurs.
(ii) For surface B, threshold frequency is equal to frequency of incident light, so emission just occurs.
(iii) For surface C, the threshold frequency is less than frequency of incident light. So, photo-emission occurs and photo-electron have some K. E.
Threshold frequency is VA > VB > Vc.

Section – D

Question 29.
Diffraction of light: The diffraction of light takes place when an object or obstacle comes in the path of light. In this phenomena bending of light takes place around the edges of the obstacle. The bending of light from its path is larger when the size of the obstacle is comparable to the wavelength of light.

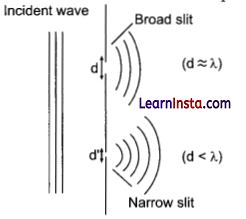
It we place a narrow slit in the path of wavefront of light, then bending of diffracted wavefront will be more. The diffraction of sound waves also takes place. For visible light, diffraction can happen when an object of λ 10^-6 m order comes in its path.
(i) The phenomenon of bending of light around the edges is called:
(a) Interference
(b) Refraction
(c) Diffraction
(d) Polarisation
Answer:
(c) Diffraction

(ii) The diffraction of an incident wave will not happen when size aperture will be:
(a) Small
(b) Very small
(c) Very large
(d) None of these
Answer:
(c) Very large

(iii) The diffraction of light waves increases as the size of aperture of a hole:
(a) Increases
(b) Both (a) and (b)
(c) Decreases
(d) Remain same
Answer:
(c) Decreases

(iv) The diffraction of light can take place through:
(a) Sharp edges
(b) Very small apertures
(c) Very large apertures
(d) Both (a) and (b)
Answer:
(d) Both (a) and (b)

OR

In which case diffraction of light will be more for an aperture (d):
(a) d>λ
(b) = λ
(c) d<λ
(d) None of these
Answer:
(c) d<λ

Question 30.
Nuclear Fission: In the year 1939, German scientist Otto Hahn and Strassmann discovered that when an uranium isotope was bombarded with a nuetron, it breaks into two intermediate mass fragments. It was observed that, the sum of the masses of new fragments formed were less than the mass of the original nuclei. This difference in the mass appeared as the energy released in the process. Thus, the phenomenon of splitting of a heavy nycleus (usually A > 230) into two or more lighter nuclei by the bombardment of proton, neutron, a-particle, etc with liberation of energy is called nuclear fission.

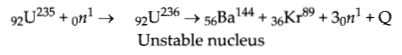
(i) Which of the following is/are fission reaction (s)?

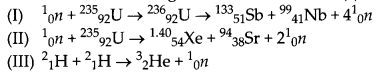
(a) Both II and III
(b) Both I and III
(c) Only II
(d) Both I and II
Answer:
(b) Both I and III

(ii) On an average, the number of neutrons and the energy of a neutron released per fission of a uranium
atom are respectively:
(a) 2.5 and 2 keV
(b) 3 and 1 keV
(c) 2.5 and 2 MeV
(d) 2 and 2 keV
Answer:
(b) 3 and 1 keV

(iii) Nuclear fission can be explained on the basis of :
(a) Millikan’s oil drop method
(b) Liquid drop model
(c) Shell model
(d) Bohr’s model
Answer:
(d) Bohr’s model

OR

For sustaining the nuclear fission chain reaction in a sample (of small size) of ²³⁵₉₂ U, it is desirable to slow down fast neutrons by :
(a) friction
(b) elastic damping/scattering
(c) absorption
(d) none of these
Answer:
(c) absorption

(iv) In any fission process, ratio of mass of daughter nucleus to mass of parent nucleus is:
(a) less than 1
(b) greater than 1
(c) equal to 1
(d) depends the mass of parent nucleus
Answer:
(a) less than 1

Section – E

Question 31.
(a) (i) Define electric flux. Is it a scalar or a vector quantity? A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown in the figure. Use Gauss’ law to obtain the expression for the electric flux through the square.

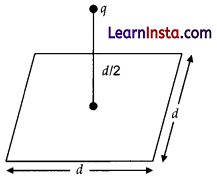
(ii) If the point charge is now moved to a distance ‘d’ from the centre of the square is doubled, explain now the electric flux will be affected?
(b) Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss’ law.

OR

(a) A charge is distributed uniformly over a ring of radius a. Obtain an expression for the electric intensity E at a point on the axis of the ring. Hence show that for points at large distances from the ring, it behaves like a point charge.
(b) Two charged spherical conductors of radii R₁ and R₂ when connected by a conducting wire acquire charge q₁ and q₂ respectively. Find the ratio of their surface charge densities in terms of their radii.
Answer:
(a) (i) Electric flux: Electric flux through an area is defined as the product of electric field strength E and area dS perpendicular to the field. It represents the field lines crossing the area. It is a scalar quantity. Imagine a cube of edge d, enclosing the charge. The square surface is one of the six faces of this cube. According to Gauss’ theorem in electrostatics.

 

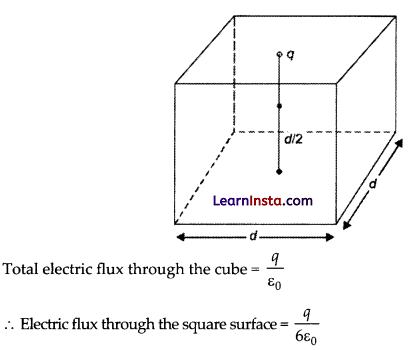
(ii) On moving the charge to distance d from the centre of square and making side of square 2d, does not change the flux at all because flux is independent of side of square or distance of charge in this case.
(b) Consider a long thin wire XY of uniform linear charge density λ [Fig. (a)].

Take a point P at perpendicular distance l from mid-point O of wire as shown in [Fig. (b)].

 

The electric field is resolved into two rectangular components. dE cos θ is the perpendicular component and dE sin θ is the parallel component. When the whole wire is considered, the component dE sin θ is cancelled. Only the perpendicular component dE cos θ affects point P.
Hence, effective electric field at point P due to the element dx is dE₁.

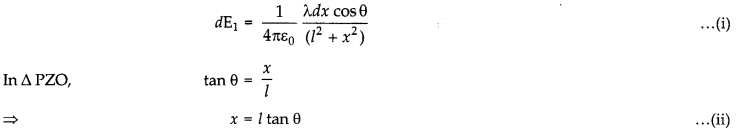
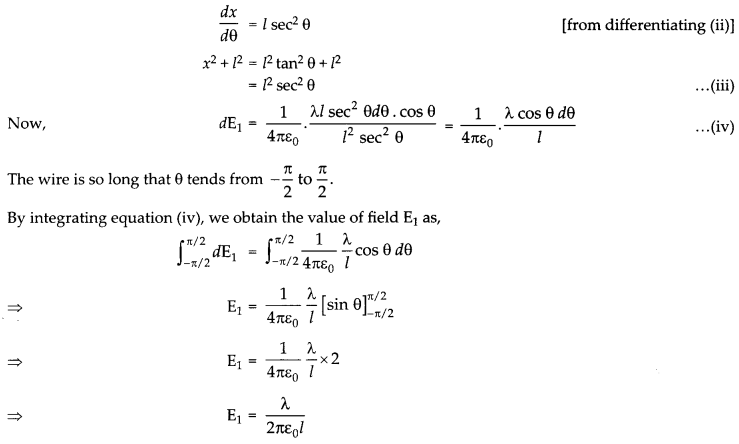
OR
(a) Suppose we have a ring of radius a that carries a uniformly distributed positive charge q.

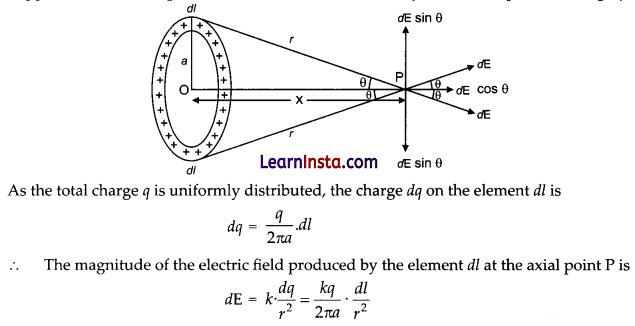
The electric field dE has two components:
(i) The axial components dE cos θ and
(ii) The perpendicular component dE sin θ.
Since, the perpendicular component of any two diametrically opposite elements are equal and opposite, they cancel out in pairs. Only the axial components will add up to produce the resultant field. E at point P is given by,

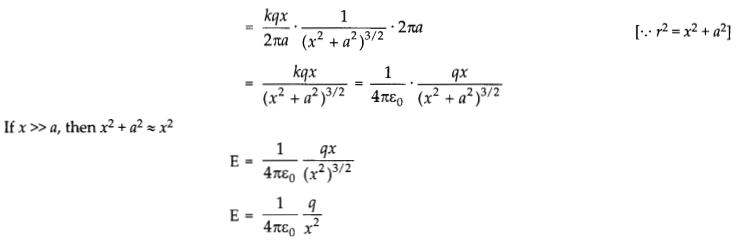
This expression is similar to electric field due to a point charge.
(b) The surface charge density for a spherical conductor of radius R₁ is given by :

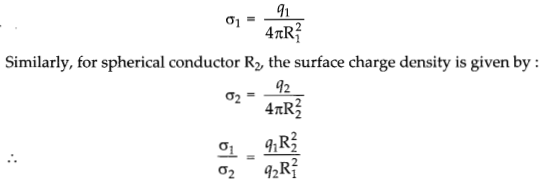
As the spheres are connected so the charges will flow between the spherical conductors till their potential become equal.

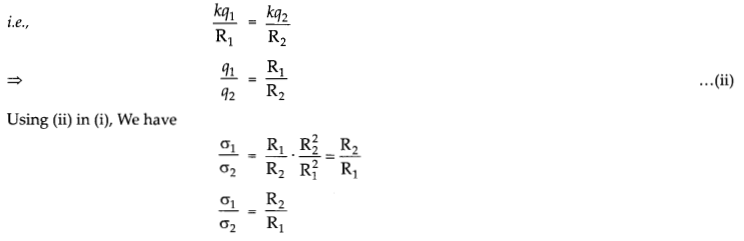
Question 32.
(a) Two point charges + Q₁ and – Q₂ are placed r distance apart. Obtain the expression for the amount of work done to place a third charge Q₃ at the midpoint of the line joining two charges.
(b) At what distance from charge + Q₁ on the line joining two charges (in terms of Q₁, Q₂ and r) will this work done by zero.
OR
Derive expression for electrostatic potential due to electric field of:
(a) Point charge
(b) Electric dipole
Answer:
According to the question,
(a) Work done :

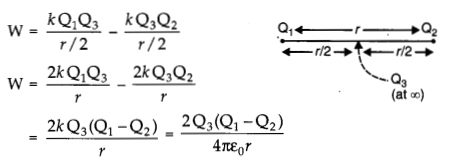
(b) For work done to be zero: Work done will be zero for the point where the electric potential is zero consider a point P to be lying in between the two charges, where electric potential is zero. Let the distance of the point P from the charge Q₁ be x.

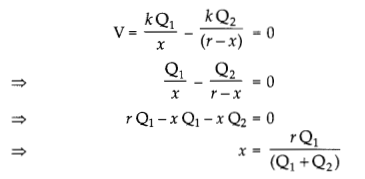
(a) The electric field at any point A having \(\vec{r}\) as its position-vector due to a point charge q placed at the origin of the coordinate system is given by,

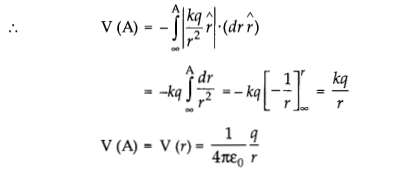
The electric potential is positive if q is positive and negative if q is negative. Hence, for negative charge negative sign should be used for q in the above equation.

(b) Electrostatic potential due to electric dipole: Let the two charges – q and + q be placed at A and B respectively with a distance 2a between them.
Let P be a unit at a distance r from the centre of this dipole and making an angle θ with its direction such that AP = r₁ and BP = r₂.

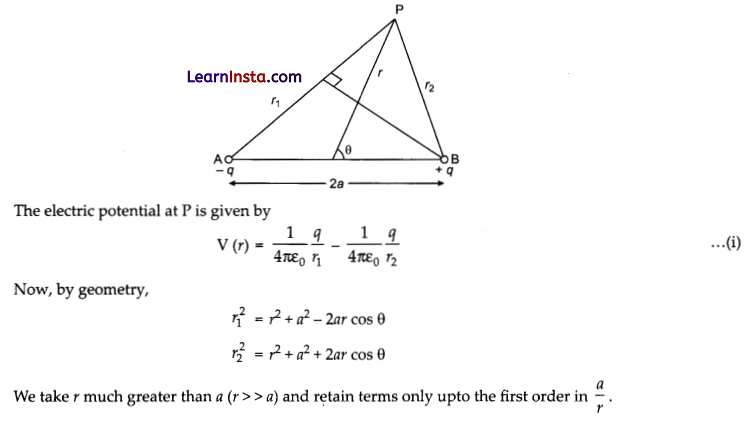
Question 33.
(a) When a convex lens of focal length 30 cm is in contact with a concave lens of focal length 20 cm, find out if the system is converging or diverging.
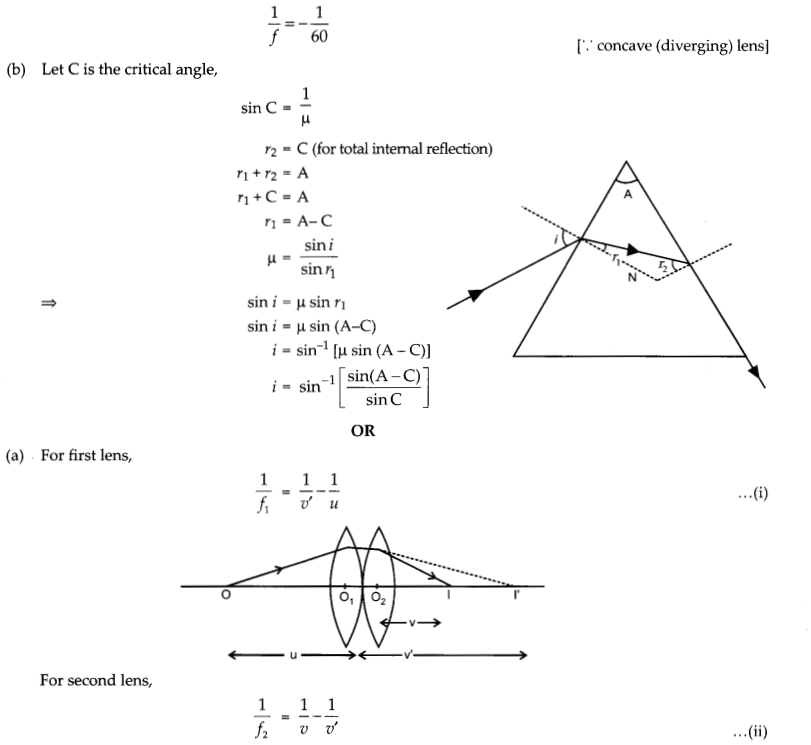
(b) Obtain the expression for the angle of incidence of a ray of light which is incident on the face of a prism of refracting angle A so that it suffers total internal reflection at the other face. (Given the refractive index of the glass of the prism is μ)
OR
(a) Draw a ray diagram to show the image formation by a combination of two thin convex lenses in contact. Obtain the expression for the power of this combination in terms of the focal lengths of the lenses.
(b) (i) Draw a ray diagram depicting the formation of the image by an astronomical telescope in normal adjustment.
(ii) You are given the following three lenses. Which two lenses will you use as an eyepiece and as an objective to construct an astronomical telescope? Give reason.

Lenses	Power (D)	Aperture (cm)
L1	3	8
L2	6	1
L3	10	1

Answer:

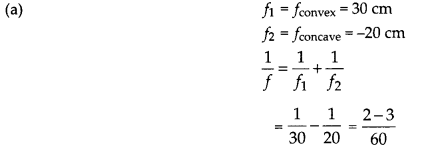
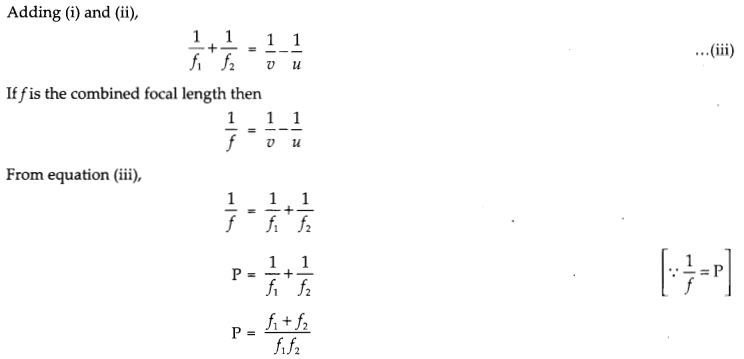
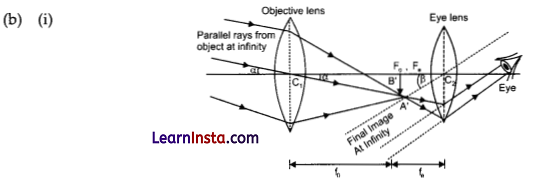
(ii) An astronomical telescope should have an objective of large aperture and longer focal length while an eyepiece of small aperture and small focal length. Therefore, we will use L₁ as an objective and L₃ as an eyepiece.