CBSE Sample Papers for Class 12 Maths Paper 4 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 4.
CBSE Sample Papers for Class 12 Maths Paper 4
| Board | CBSE |
| Class | XII |
| Subject | Maths |
| Sample Paper Set | Paper 4 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 4 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.
Time: 3 Hours
Maximum Marks: 100
General Instructions:
- All questions are compulsory.
- Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
- Questions 5-12 in section B are short answer type questions carrying 2 marks each.
- Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
- Questions 24-29 in section D are long answer II type questions carrying 6 marks each.
SECTION A
Question 1.
Find the principal value of \({ cos }^{ -1 }\left( cos\frac { 7\pi }{ 6 } \right)\)
Question 2.
A and B are square matrices of order 3 each |A| = 2 and |B| = 3, find |3AB|.
Question 3.
If \(\vec { a } =2\hat { i } -\hat { j } +3\hat { k }\) and \(\vec { b } =6\hat { i } +\lambda \hat { j } +9\hat { k }\) and \(\vec { a } ||\vec { b }\), find the value of X.
Question 4.
If f(x) = x + 7 and g (x) = x – 7, find fog (7).
SECTION B
Question 5.
Differentiate cos-1(ex) with respect to ex.
Question 6.
Find the sum of the order and the degree of the differential equation.
Question 7.
Question 8.
How many equivalence relations on the set {1, 2, 3} containing (1, 2) and (2, 1) are there in all?
Question 9.
Find the direction cosines of the normal to the plane 2x + 3y – z = 5 and also find the distance from the origin.
Question 10.
A shopkeeper sells only tables and chairs. He has only ₹ 6000 to invest and has space for atmost 20 items. A table costs him ₹ 400 and a chair ₹ 250. He can sell a table at a profit of ₹ 25 and a chair at a profit of ₹ 40. Supposing that he sell all his stock, formulate the problem as L.F.P.
Question 11.
The sides of an equilateral triangle are increasing at the rate of 2 cm/sec. Find the rate at which its area increases when side is 10 cm long.
Question 12.
A couple has 2 children. Find the probability that both are boys if it is known that
(i) atleast one of them is a boy
(ii) the older child is a boy.
SECTION C
Question 13.
Question 14.
Evaluate \(\int _{ 0 }^{ 3 }{ \left( { x }^{ 2 }-5 \right) } dx\)
Question 15.
Find the area of the region bounded by the curve \(y=\sqrt { 1-{ x }^{ 2 } }\) and the line y = x bounded with positive x-axis.
Question 16.
Determine for what values of x the function f(x) = x3 + \(\frac { 1 }{ { x }^{ 3 } }\), x ≠ 0 is strictly increasing or strictly decreasing.
OR
Find the point on the curve y = x3 – 11x + 5 at which the tangent is y = x – 11.
Question 17.
It is given that for the function f(x) = x3 – 6x2 + ax + b Rolle’s theorem verified in [1, 3] with c = 2 + \(\frac { 1 }{ \surd 3 }\). Find the value of a and b.
Question 18.
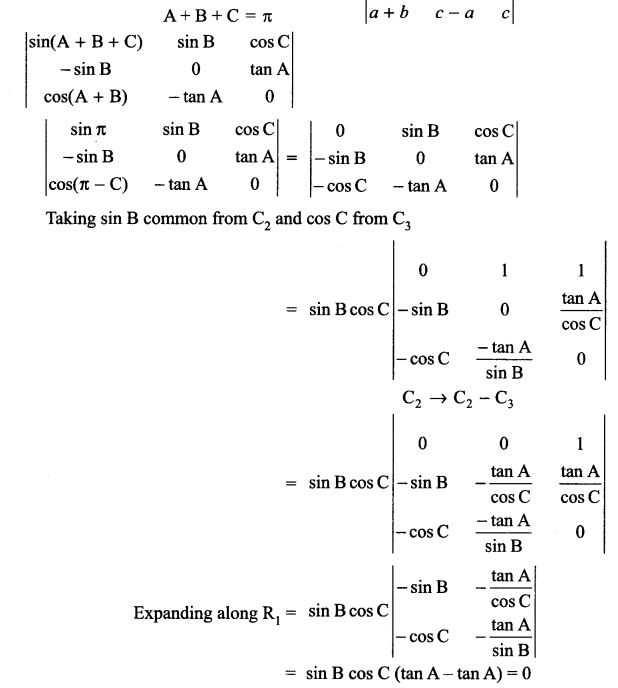
If A + B + C = π then find the value of
OR
Using properties of determinant prove that
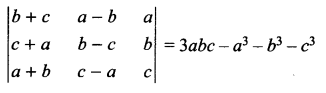
Question 19.
Find the Cartesian as well as the vector equation of the plane passing through the intersection of the planes \(\vec { r } \cdot \left( 2\hat { i } +6\hat { j } \right) +12=0\) and \(\vec { r } \cdot \left( 3\hat { i } -\hat { j } +4\hat { k } \right) =0\) which are at unit distance from the origin.
Question 20.
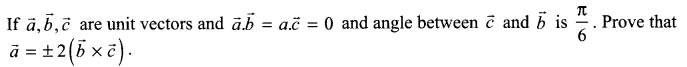
Question 21.
For three persons A, B, C the chances of being selected as manager of a firm are in the ratio 4 : 1 : 2 respectively. The respective probabilities for them to introduce new changes in market strategy are 0.3, 0.8 and 0.5 respectively. If the changes does take place find the probability that it was due to appointment of B or C. Write the qualities that makes a person successful manager.
Question 22.
Using graphical method solve the following L.P.P.
Z = 4x + 8y
Subject to constraints
2x + y ≤ 30
x + 2y ≤ 24
x ≥ 3, y ≤ 9, y ≥ 0
Question 23.
Suppose that 80% of the people are right handed. What is the probability that at most 6 of at random samples of 10 people are right-handed?
SECTION D
Question 24.
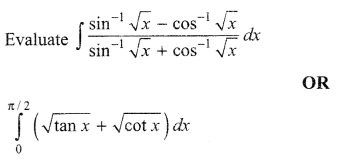
Question 25.
Does the following trigonometric equation have any solution? If yes, obtain the solutions \({ tan }^{ -1 }\left( \frac { x+1 }{ x-1 } \right) +{ tan }^{ -1 }\left( \frac { x-1 }{ x } \right) =-{ tan }^{ -1 }7\)
OR
Determine whether the operation * define on Q is binary operation or not. a * b = ab + 1. If yes, check the commutative and associative properties. Also check the existence of identity element and the inverse of all elements in Q.
Question 26.
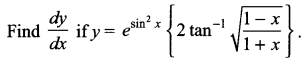
Question 27.
Find the shortest distance between the line x – y + 1 = 0 and the curve y2 = x.
Question 28.
Find the distance of the point (-2, 3, -4) from the line \(\frac { x+2 }{ 3 } =\frac { 2y+3 }{ 4 } =\frac { 3z+4 }{ 5 }\) measured parallel to the plane 4x + 12y – 3z + 1 = 0.
Question 29.
If \(A=\left( \begin{matrix} 2 & 3 & 7 \\ 3 & -2 & -1 \\ 1 & 1 & 2 \end{matrix} \right)\) , find A-1.
Using A-1 solve the following system of equations
2x + 3y + 7z = 12
3x – 2y – z = 0
x + y + 2z = 4

Solutions
Solution 1.
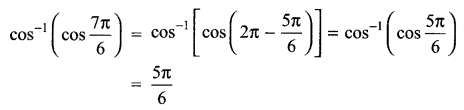
Solution 2.
|3AB| = 33 |A| |B| = 27 (2) (3) = 162
Solution 3.
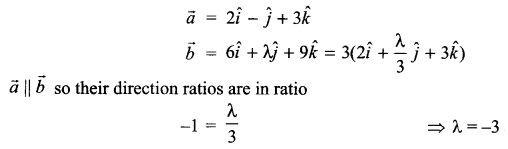
Solution 4.
f(x) = x + 7, g(x) = x – 7
(fog) (x) = f(g(x)) = f(x – 7) = x – 7 + 7 = x
(fog) (7) = 7.
Solution 5.
Let y = cos-1 (ex) and t = ex
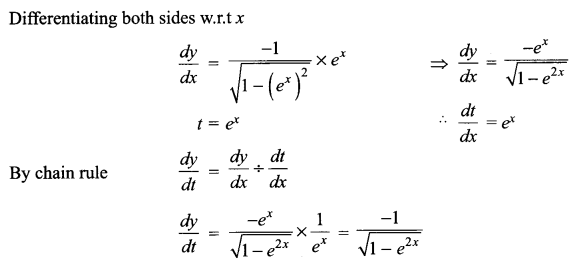
Solution 6.
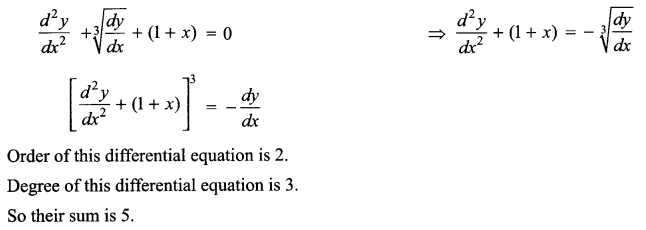
Solution 7.
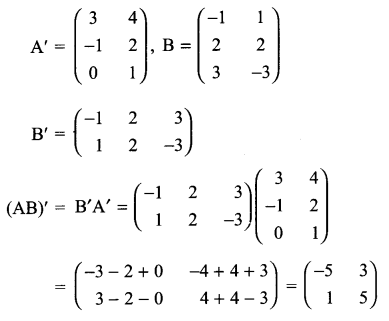
Solution 8.
Possible equivalence relations are {(1, 2), (2, 1), (1, 1), (2, 2), (3, 3)} and {(1, 1), (2, 2), (3, 3), (1, 2),(2, 1), (1, 3), (3, 1), (2, 3), (3, 2)}
There are two possible equivalence relation.
Solution 9.
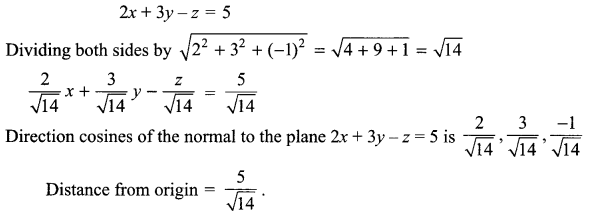
Solution 10.
Let shopkeeper sales x tables and y chairs.
Objective function is Maximize Profit Z = 25x + 40y
Subject to constraints are
400 x + 250 y ≤ 6000 (investment constraint)
x + y ≤ 20 (space constraint)
x, y ≥ 0 (Non-negative constraint)
Solution 11.
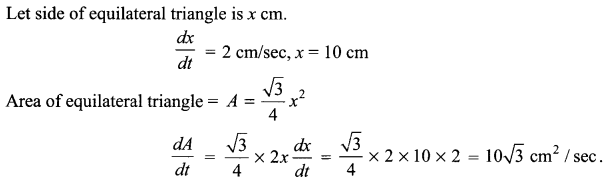
Solution 12.
As per order of birth two children may be (B1B2, G1G2, B1G2, G1B2}
Let E is the event both are boys ⇒ (B1B2)
E1 is the event atleast one of them is a boy ⇒ (B1B2, B1G2, G1B2)
E2 is the event the older child is a boy ⇒ (B1B2, B1G2)
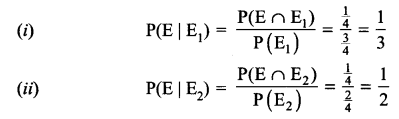
Solution 13.


Solution 14.
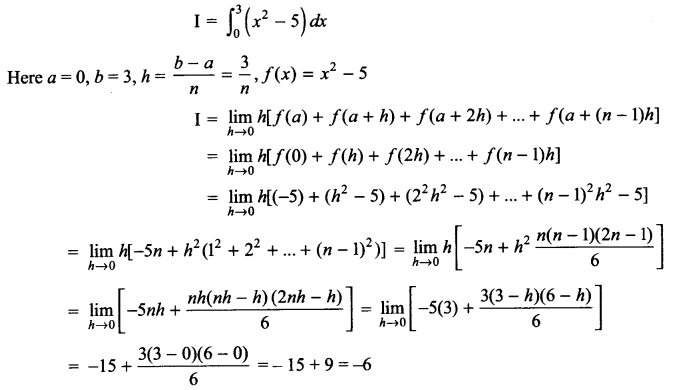
Solution 15.
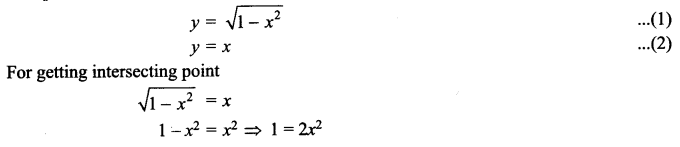
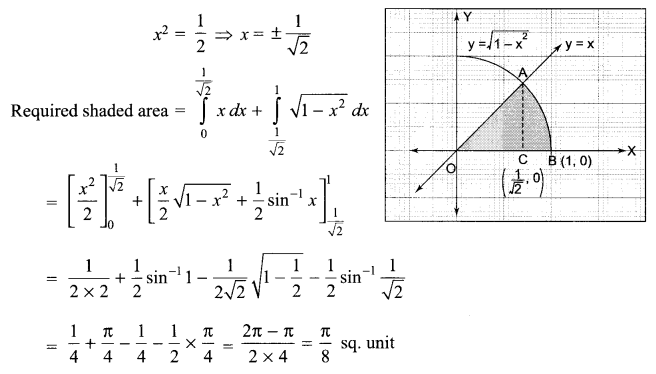
Solution 16.

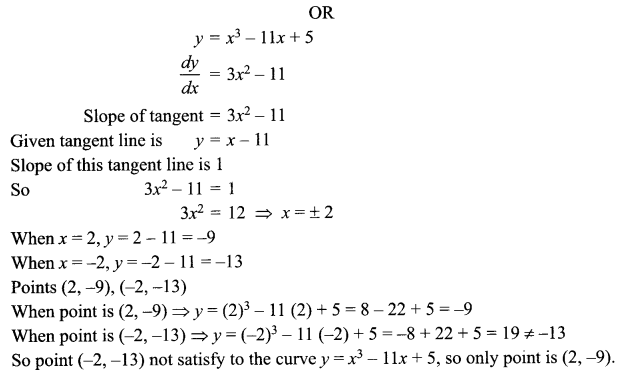
Solution 17.

Solution 18.
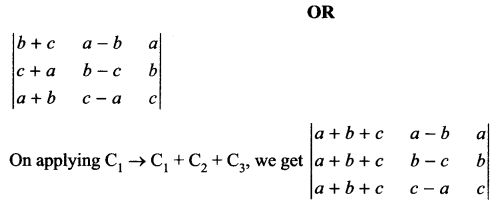

Solution 19.
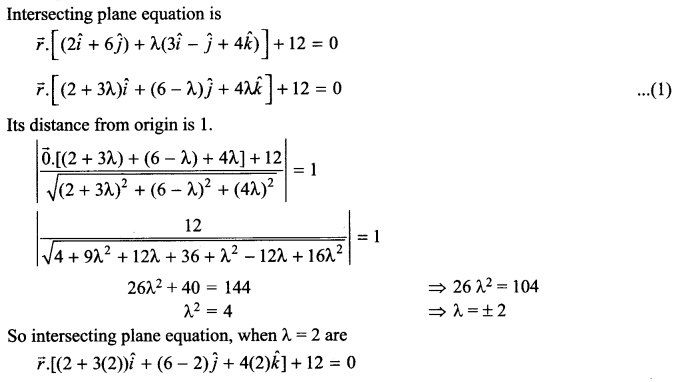
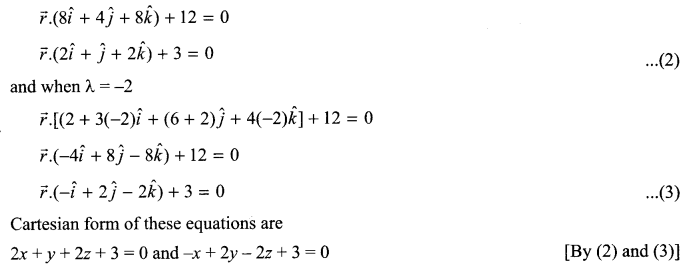
Solution 20.
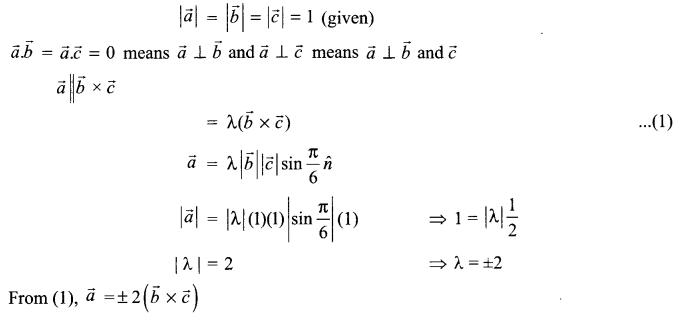
Solution 21.

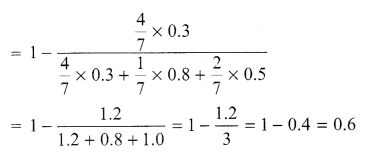
Solution 22.
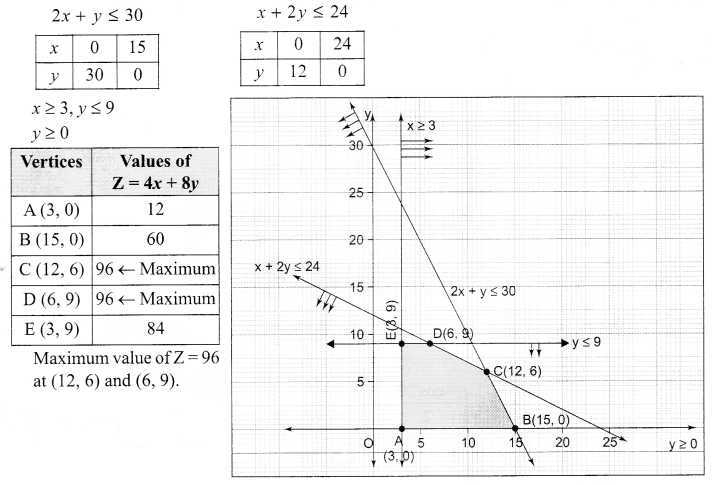
Solution 23.
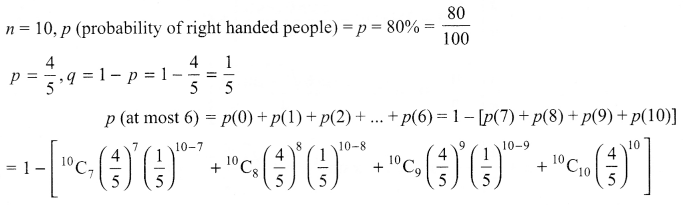
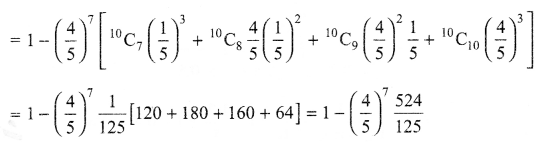
Solution 24.
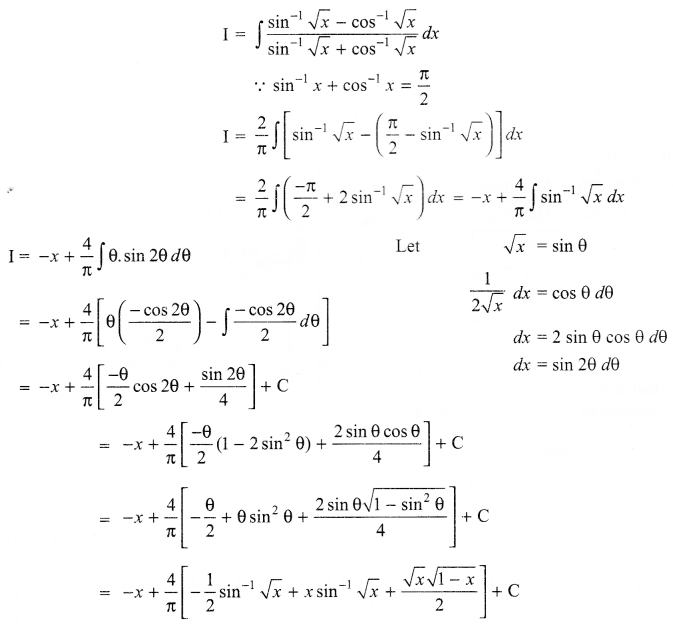
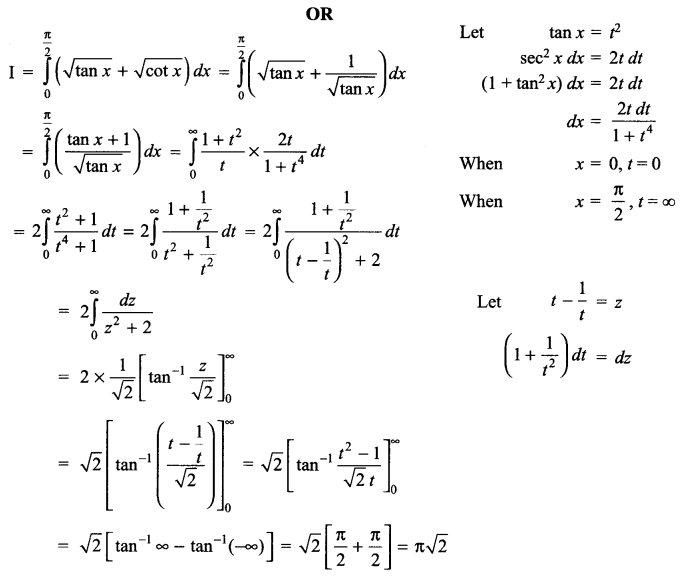
Solution 25.
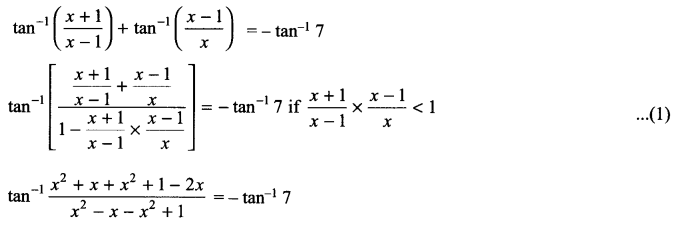
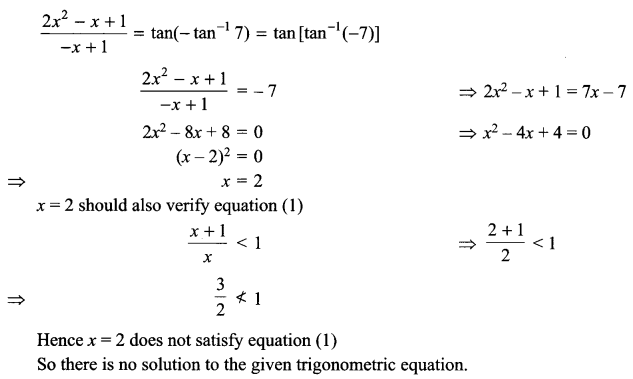

Solution 26.
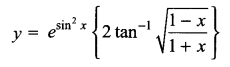
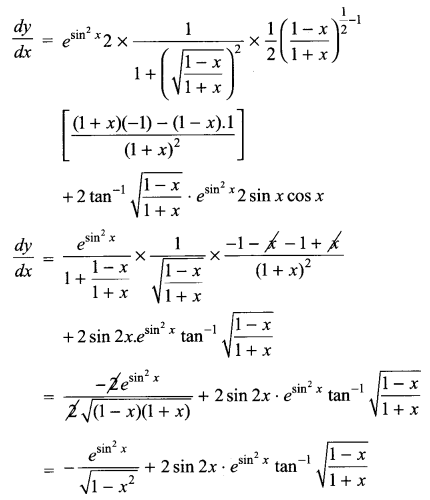
Solution 27.

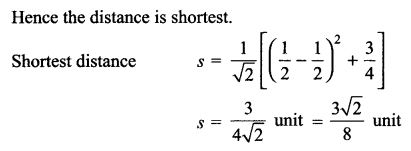
Solution 28.

Solution 29.
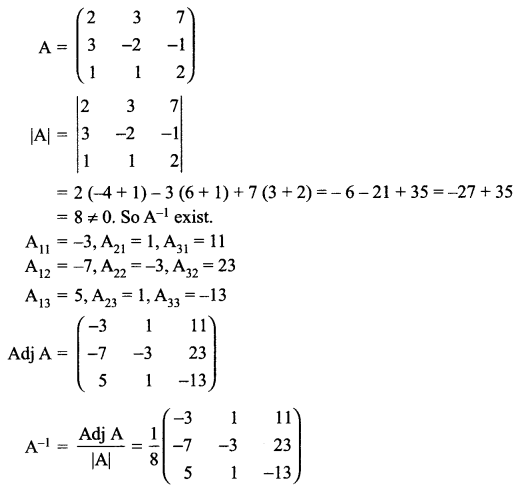
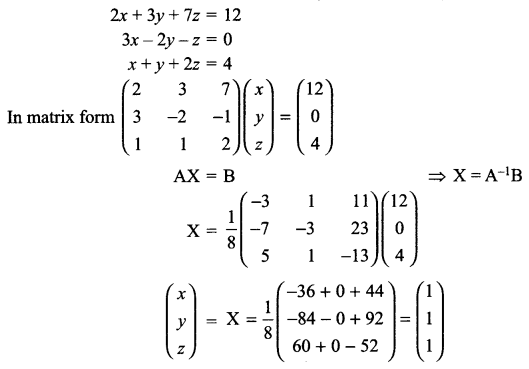
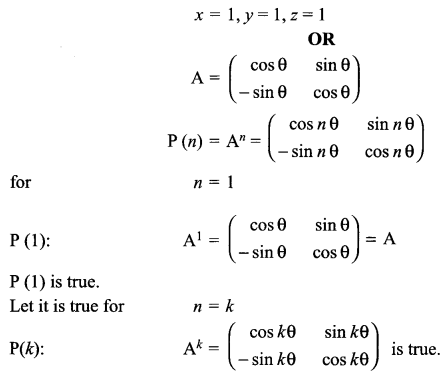
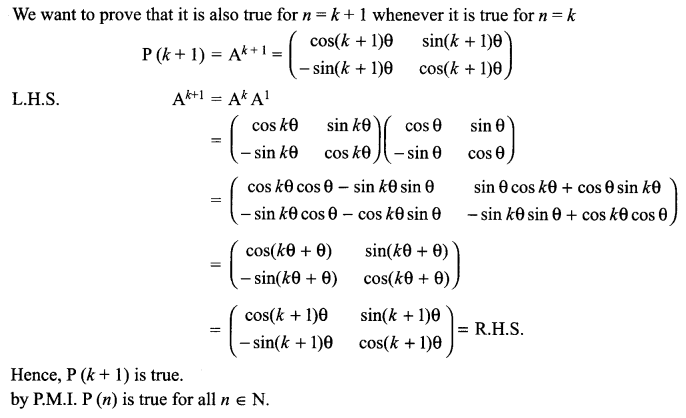
We hope the CBSE Sample Papers for Class 12 Maths Paper 4 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 4, drop a comment below and we will get back to you at the earliest.