CBSE Sample Papers for Class 12 Applied Maths Set 4 with Solutions

Students can access the CBSE Sample Papers for Class 12 Applied Maths with Solutions and marking scheme Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Maths Set 4 with Solutions

Time Allowed : 3 hours
Maximum Marks : 80

General Instructions:

1. This Question paper contains – five sections A,B,C,D and E. Each section is compulsory. However, there is some internal ‘ choice in some questions.
2. Section A has 18 MCQ’s and 02 Assertion Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) questions of 2 marks each.
4. Section C has 6 Short Answer (SA) questions of 3 marks each.
5. Section D has 4 Long Answer (LA) questions of 5 marks each.
6. Section E has 3 source based/case based/passage based/integrated units of assessment (04 marks each) with sub parts.
7. Internal Choice is provided in 2 questions in Section-B, 2 questions in Section-C, 2 Questions in Section-D. You have to attempt only one alternatives in all such questions.

Section – A
(All Questions are compulsory. No internal choice is provided in this section)

Question 1.
If the present time is 8:40 pm, then the time after 876\(\frac{1}{2}\) hours will be
(A) 8:40 am
(B) 9:10 am
(C) 6:10 pm
(D) 10:40 pm
Answer:
(B) 9:10 am

Explanation:
876 (mod 24) = 12
∴ 8 : 40 pm will change to 8:40 am after 12 hours, further after 30 minutes the time will be 9:10 am.

Question 2.
Let p > 0 and q < 0 and p, q ∈ Z, then choose the correct inequality from the given below options to complete the statements: p + q _______ p – q
(A) >
(B) ≤
(C) ≥
(D) <
Answer:
(D) <

Explanation:
Here, p + q is less than p – q as given q is negative.

Question 3.
Standard deviation of a sample from a population is called a
(A) Standard error
(B) Parameter
(C) Statistic
(D) Central limit
Answer:
(C) Statistic

Question 4.
A sample of 100 wall clocks is taken at random. Out of 100 we found 25 wall clocks are digital and 75 are analogue. The point estimate of population proportion of analogue is
(A) 0.25
(B) 0.50
(C) 0.75
(D) None of these
Answer:
(C) 0.75

Explanation:
Population proportion for analogue = \(\frac{75}{100}\) = 0.75

Question 5.
Two water supplying trucks – A and B supply water to remote areas. Truck A is carrying 100 litres of water to a village 1.5 km away and truck B is delivering 80 litres of water to another village, 1 km away. Due to bad road conditions, each truck loses 20 ml water while travelling each metre distance. Which truck is able to deliver more water and by how much more?
(A) Truck A, 20 litres
(B) Truck B, 20 litres
(C) Truck A, 10 litres
(D) Truck B, 10 litres
Answer:
(C) Truck A, 10 litres

Explanation:
Truck A cames water = 100 – \(\frac{20 \times 1500}{1000}\) = 70 l
Truck B carries water = 80 – \(\frac{20 \times 1000}{1000}\) = 60 l

Question 6.
Let X denotes the number of hours a student devotes to self-study during a randomly selected school day. The probability that X takes the value x, where k is some unknown constant is
P (X = x) = \(\left\{\begin{array}{ccc}
k & \text { if } & x=0 \\
k x & \text { if } & x=1 \text { or } 2 \\
k(5-x) & \text { if } & x=3 \text { or } 4 \\
0 & & \text { otherwise }
\end{array}\right.\)

The probability that a student studies at least 3 hours on a particular day is
(A) \(\frac{1}{7}\)
(B) \(\frac{2}{7}\)
(C) \(\frac{3}{7}\)
(D) \(\frac{1}{2}\)
Answer:
(C) \(\frac{3}{7}\)

Explanation:
Σp_i =1
⇒ 7k = 1
⇒ k = \(\frac{1}{7}\)
Now, P(x ≥ 3) = 3k
= 3 × \(\frac{1}{7}\)
= \(\frac{3}{7}\)

Question 7.
What is the least value of ‘x’ that satisfies x = 27(mod 4), when 27 < 1 ≤36?
(A) 27
(B) 30
(C) 31
(D) 35
Answer:
(C) 31

Explanation:
x = 27 (mod 4)
⇒ x – 27 = 4k, for some integer k
⇒ x = 31 as 27 < x ≤ 36

Question 8.
₹ 2,50,000 cash is equivalent to a perpetuity of ₹ 7,500 payable at the end of each quarter. The rate of interest convertible quarterly is
(A) 7% p.a.
(B) 9% p.a.
(C) 11.5% p.a.
(D) 12% p.a.
Answer:
(D) 12% p.a.

Explanation:
P = 250000,
R = 7500,
i = \(\frac{r}{400}\)
⇒ 250000 = \(\frac{7500 \times 400}{r}\)
⇒ r = 12% p.a.

Question 9.
In the given figure, the area bounded by the curve x = f(y), Y-axis and abscissa y = a and y = b is equal to

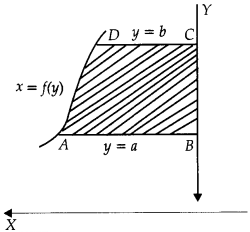
(A) \(\int_a^b\) f(y) dy
(B) \(\int_a^b\) |f(y)| dy
(C) \(\int_a^b\) f(x) dx
(D) \(\int_a^b\) |f(x)| dx
Answer:
(C) \(\int_a^b\) f(x) dx

Question 10.
For predicting the straight-line trend in the sales of scooters (in thousands) on the basis of 6 consecutive years data, the company makes use of 4-year moving averages method. If the sales of scooters for respective years are a, b, c, d, e and f respectively, then which of the following average will not be computed?
(A) \(\frac{a+b+c+d}{4}\)
(B) \(\frac{b+c+d+e}{4}\)
(C) \(\frac{a+c+d+e}{4}\)
(D) \(\frac{c+d+e+f}{4}\)
Answer:
(C) \(\frac{a+c+d+e}{4}\)

Question 11.
A washing machine costing ₹ 25,000 is expected to have a useful life of 7 years and a final scrap value of ₹ 2000. The annual depreciation charge using the straight line method is
(A) 3,000
(B) 3,500
(C) 3,826
(D) 3,906
Answer:
(C) 3,826

Explanation:
Annual depreciation = \(\frac{\text { Cost -Scrap Value }}{\text { Useful life }}\)
= \(\frac{25,000-2,000}{7}\)
= \(\frac{23,000}{7}\)
= ₹ 3,285.71 ~ ₹ 3,286.

Question 12.
An investment’s starting value is ₹ 15,000 and it grows to ₹ 75,000 in 5 years, then its compound annual growth rate is: [Given 5^{\(\frac{1}{5}\)} = 1.379 ]
(A) 37 %
(B) 38 %
(C) 39 %
(D) 40%
Answer:
(B) 38 %

Explanation:
CAGR = \(\left[\left(\frac{\text { Final investment value }}{\text { Initial investment value }}\right)^{\frac{1}{n}}-1\right]\) × 100
= \(\left[\left(\frac{75,000}{15,000}\right)^{\frac{1}{5}}-1\right]\) × 100
= [\((5)^{\frac{1}{5}}\) – 1] × 100
= (1.379 – 1) × 100
= 37.9 % ≈ 38 %

Question 13.
At 7% converted quarterly, the present value of a perpetuity of ₹ 700 payable at the end of each quarter is
(A) ₹ 30,000
(B) ₹ 45,000
(C) ₹ 40,000
(D) ₹ 50,000
Answer:
(C) ₹ 40,000

Explanation:
Given, R = 700,
i = \(\frac{0.07}{4}\) = 0.0175
The present value of a perpetuity,
P = \(\frac{R}{i}\)
= \(\frac{700}{0.0175}\)
= ₹ 40,000

Question 14.
The order and degree (if defined) of differential equation y dx + [x log (\(\frac{y}{x}\) ) – 2x] dy = 0 are
(A) 1, 1
(B) 1, 0
(C) 0, 1
(D) Not defined
Answer:
(A) 1, 1

Explanation:
Given differential equation,
y dx + [x log (\(\frac{y}{x}\)) – 2x] dy = 0
⇒ [2x – x log (\(\frac{y}{x}\))] dy = y dx
⇒ \(\frac{d y}{d x}=\frac{y}{2 x-x \log \left(\frac{y}{x}\right)}\)
The highest order derivative present is \(\frac{d y}{d x}\) and it is raised to power 1.
So, its order is 1 and degree is also 1.

Question 15.
For the constraint of a linear optimizing function z = x₁ + x₂, given by x₁ + x₂ < 1, 3x₁ + x₂ > 3 and x₁, x₂ ≥ 0
(A) There are two feasible regions
(B) There are infinite feasible regions
(C) There is no feasible region
(D) None of these
Answer:
(C) There is no feasible region

Explanation:
Clearly from graph there is no feasible region.

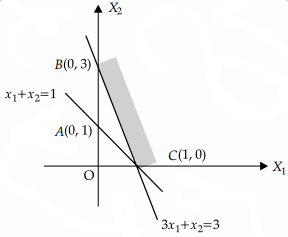
Question 16.
If a random variable X has the Poisson distribution with mean 2. Then, P(X > 1.5) is
(A) 2e^-2
(B) 3e^-2
(C) 1 – 2e^-2
(D) 1 – 3e^-2
Answer:
(D) 1 – 3e^-2

Explanation:
We know that,
P(X = x) = \(\frac{e^{-\lambda} \lambda^x}{x !}\)
Given that mean = 2 = λ
∴ P(X > 1.5) = P(X = 2) + P(X = 3) + ………..
⇒ P(X > 1.5) = 1 – [P(X = 0) + P(X = 1)]
= 1 – [e^-2 + 2e^-2]
= 1 – 3e^-2

Question 17.
An orderly set of data arranged in accordance with their time of occurrence is called
(A) Arithmetic Series
(B) Geometric Series
(C) Harmonic Series
(D) Time Series
Answer:
(D) Time Series

Explanation:
The organized series of data on the basis of any measure of time is called Time series.

Question 18.
For the purpose of t-test of significance, a random sample of size (n) 34 is drawn from a normal population, then the degree of freedom (v) is:
(A) \(\frac{1}{34}\)
(B) 33
(C) 34
(D) 35
Answer:
(B) 33

Explanation:
n = 34
⇒ v = 34 – 1 = 33

DIRECTION:
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.

Question 19.
Assertion (A) : 2 is least value of a function such that the function f given by f(x) = x² + ax + 1 is strictly increasing on (1, 2).
Reason (R) : – 2 is the least value of a function f given by f(x) = x² + ax + 1 is strictly increasing on (1, 2).
Answer:
(D) (A) is false but (R) is true.

Explanation:
f(x) = x² + ax + 1
∴ f(x) = 2x + a
Now, function fis strictly increasing in (1, 2).
i.e., f'(x) > 0
∴ 2x + a > 0
⇒ a > – 2x
∴ We have to find least value of a, such that
x ∈ (1, 2)
∴ a > – 2
a ∈ (- 2, ∞)
So, least value of a is – 2.

Question 20.
Assertion (A) : Kuhu and Beena are two equally capable badminton players. Probability that Beena will beat Kuhu in 3 games out of 4 is 25%.
Reason (R) : The probability of r successes in n trials, denoted by P(X = r) is given by P(X = r) = \(\) p^r q^n-r, r = 0, 1, ……, n where p denotes success and q denotes failure in each trial.
Answer:
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).

Explanation:
P(Win in one game) = P(lose in one game) = \(\frac{1}{2}\)
⇒ P(Beena to win in 3 out of 4 games)
= \({ }^4 C_3 \cdot\left(\frac{1}{2}\right)^3\left(\frac{1}{2}\right)^1\)
= 4 × \(\left(\frac{1}{2}\right)^4\)
= \(\frac{1}{4}\) = 25 %

Section – B
(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 21.
Mitul invested ₹ 3,50,000 in a fund. At the end of the year the value of the fund is ₹ 4,37,500. What is the nominal rate of interest, if the market price is same at the end of the year?
Answer:
V_f = 437500
V_i = 350000
nominal rate = \(\frac{V_f-V_i}{V_i}\) × 100
= \(\frac{437500-350000}{350000}\) × 100
= 25 %

OR

Question 22.
Find the value of 2a + 3b – c, if A = \(\left[\begin{array}{ccc}
0 & -1 & 28 \\
a-8 & 0 & 3 b \\
-c+2 & 2 & 0
\end{array}\right]\) is a skew-symmetric matrix.
Answer:
For skew symmetric matrix, A = – A’
i.e., \(\left[\begin{array}{ccc}
0 & -1 & 28 \\
a-8 & 0 & 3 b \\
-c+2 & 2 & 0
\end{array}\right]=-\left[\begin{array}{ccc}
0 & a-8 & -c+2 \\
-1 & 0 & 2 \\
28 & 3 b & 0
\end{array}\right]\)
Or, \(\left[\begin{array}{ccc}
0 & -1 & 28 \\
a-8 & 0 & 3 b \\
-c+2 & 2 & 0
\end{array}\right]=\left[\begin{array}{ccc}
0 & -a+8 & c-2 \\
1 & 0 & -2 \\
-28 & -3 b & 0
\end{array}\right]\)
On comparing matrices, we get
a – 8 = 1
⇒ a = 9
3b = – 2
⇒ b = – \(\frac{2}{3}\)
– c + 2 = – 28
⇒ c = 30
2a + 3b – c = – 14

OR

If A is a square matrix satisfying AA’ = I, write the value of | A |.
Answer:
Let the value of |A| =x
Since, |A| = |A’| and |I| = 1
Given, AA’ = 1
∴ |AA’| = |I|
⇒ |A| |A’| = |I|
[|AA’| = |A| |A’|]
⇒ x . x = 1
⇒ (x² – 1) = 0
⇒ (x – 1) (x + 1) = 0
⇒ x = ± 1
∴ Value of |A| = ± 1.

Question 23.
A manufacturer produces two types of steel trunks. He has two machines, A and B. The first type of trunk requires 3 hours on machine A and 3 hours on machine B. The second type requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of ₹ 30 per trunk on the first type of trunk and ₹ 25 per trunk on the second type. Formulate a Linear Programming Problem.
Answer:
Let x units of A type
and y units of B type be produced.
∴ Max Z = 30x + 25y
Under the following restrictions
3x + 3y ≤ 18
3x + 2y ≤ 15
x ≥ 0 . y ≥ 0

Question 24.
A boatman takes half as much time in rowing his boat for a certain distance downstream than upstream. What is the ratio between his speed of rowing the boat in still water and speed of current?
Answer:
Speed of boat in still waters = x km/h
Speed of stream = y km/h
Distance travelled = d km
Time taken to travel downstream = \(\frac{d}{x+y}\)
Time taken to travel upstream = \(\frac{d}{x-y}\)
Then,
\(\frac{2 d}{x+y}=\frac{d}{x-y}\)
x : y = 3 : 1

OR

Solve the linear inequality |x – 2| ≥ 6
Answer:
We know that if I x ≥ a then x ≤ – a or x ≥ a
Therefore, |x – 2| ≥ 6
⇒ x – 2 ≤ – 6 or x – 2 ≥ 6
⇒ x≤ – 4 or x ≥ 8
⇒ – 4 ≤ x < 8
⇒ x ∈ (- ∞, – 4] ∪ [8, ∞)
Hence, the solution set of the inequation is (- ∞, – 4] ∪ [8, ∞).

Question 25.
A sample of 1000 students whose mean weight is 119 lbs (pounds) from a school in Uttar Pradesh State was taken and their average weight was found to be 120 lbs with a standard deviation of 30 lbs. Calculate the standard error of the mean.
Answer:
Given, n = 1000,
mean = 119,
σ = 30
S.E = \(\frac{\sigma}{\sqrt{n}}\)
= \(\frac{30}{\sqrt{1000}}\)
= \(\frac{30}{31.623}\)
= 0.9487

Section – C
(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 26.
Evaluate: \(\int \frac{d x}{\left(1+e^x\right)\left(1+e^{-x}\right)}\)
Answer:
\(\int \frac{d x}{\left(1+e^x\right)\left(1+e^{-x}\right)}=\int \frac{e^x d x}{\left(1+e^x\right)^2}\)
= ∫ \(\frac{d t}{t^2}\)
where t = e^x + 1
ans dt = e^x dx
= \(\frac{-1}{t}\) + C
= \(\frac{-1}{1+e^x}\) + C

OR

Evaluate: \(\int_1^2 \frac{\sqrt{x}}{\sqrt{3-x}+\sqrt{x}}\) dx.
Answer:
Let I = \(\int_1^2 \frac{\sqrt{x}}{\sqrt{3-x}+\sqrt{x}}\) dx
Using properties,

Question 27.
For what values of a and b, the system of equations
2x + ay + 6z = 8
x + 2y + bz = 5
x + y + 3z = 4
has (i) unique solution
(ii) no solution?
Answer:
For the given system of equations, we have
D = \(\left|\begin{array}{lll}
2 & a & 6 \\
1 & 2 & b \\
1 & 1 & 3
\end{array}\right|\)
= 2(6 – b) – a (3 – b) + 6 (1 – 2)
= 12 – 2b – 3a + ab – 6
= 6 – 3a – 2b + ab
= (b – 3) (a – 2)

D_x = \(\left|\begin{array}{lll}
8 & a & 6 \\
5 & 2 & b \\
4 & 1 & 3
\end{array}\right|\)
= 8 (6 – b) – a (15 – 4b) + 6 (5 – 8)
= 48 – 8b – 15a + 4ab – 18
= 30- 15a – 8b + 4ab
= (a – 2) (4b – 15)

D_y = \(\left|\begin{array}{lll}
2 & 8 & 6 \\
1 & 5 & b \\
1 & 4 & 3
\end{array}\right|\)
= 2(15 – 4b) – 8 (3 – b) + 6 (4 – 5)
= 30 – 8b – 24+ 8b – 6
= 0

D_z = \(\left|\begin{array}{lll}
2 & a & 8 \\
1 & 2 & 5 \\
1 & 1 & 4
\end{array}\right|\)
= 2(8 – 5) – a (4 – 5) + 8 (1 – 2)
= 6 + a – 8
= a – 2

(i) For unique solution, we must have D ≠ 0
⇒ (a – 2) (b – 3) ≠ 0
⇒ a ≠ 2 or b ≠ 3.

(ii) For no solution, we must have D = 0
and at least one of D_x, D_y and D_z is non-zero.
Clearly, b = 3, we have
D=Oand D_z ≠ 0
Hence, the system has no solution for b = 3.

Question 28.
Find the interval (s) in which the function f(x) = \(\frac{x^4}{4}-2 x^3+\frac{11 x^2}{2}-6 x\), is strictly increasing and strictly decreasing.
Answer:
f(x) = \(\frac{x^4}{4}-2 x^3+\frac{11 x^2}{2}-6 x\)
f'(x) = x³ – 6x² + 11x – 6
= x² (x – 1) – 5x (x-1) + 6 (x-1)
= (x – 1) (x² – 5x + 6)
= (x – 1) (x – 2) (x – 3)

For increasing f'(x) > 0
(1, 2) ∪ (3, ∞)
For decreasing f'(x) < 0
(- ∞, 1) ∪ (2, 3).

Question 29.
The demand and supply function of an article are D(q) = 1000 – 0.4q² and S(q) = 42q. Find the producer’s surplus at equilibrium price.
Answer:
D(q) = 1000 – 0.4q² and S(q) = 42q
At equilibrium d(q) = S(q)
1000 – 0.4 q² = 42q
Or, 0.4q² + 42q – 1000 = 0
Or, 4q² + 420q – 10000 = 0
Or, q² + 105q – 2500 = 0
Or, (q + 125) (q – 20) = 0
q = – 125 or 20
The value of q cannot be negative, q = 20
When q = Q_e = 20
D(20) = 1000 – 0.4 (20)²
= 1000 – 0.4 × 400
= 1000 – 160
= 840 = P
Producer’s surplus is given by
PS = Q_e . P_e – \(\int_0^{Q_e}\) S(x) dx
= 20 × 84o – \(\int_0^{20}\)42 q dq
= 16800 – 42 \(\left[\frac{q^2}{2}\right]_0^{20}\)
= 16800 – 42 \(\left(\frac{20^2}{2}-0\right)\)
=16800 – 21 × 400
=16800 – 8400
= 8400 units
Hence, at equilibrium price, the producer’s surplus is 8400 units.

OR

Rakesh and Kartik are final year engineering students. Both are selected in their campus interviews and got placement in a reputed company. But both of them decide to start their own business. For this they are surveying the market. During their survey they find the demand curve for a certain item is
p = D(q) = \(\frac{20}{q+1}\)
and the supply curve is p = S(q) = q + 2
Find consumer’s surplus. [Given log_e 2 = 0.6932]
Answer:
At the equilibrium point, supply and demand curves meet.
So, D(q) = S(q)
\(\frac{20}{q+1}\) = q + 2
Clearing the denominator gives 20 = (q + 1) (q + 2),
which simplifies to q² + 3q – 18 = 0
The positive solution gives the equilibrium quantity q_e = 3.
Put q =3 in D(q) or S(q) to get equilibrium price (p_e)
S(3) = 3 + 2 = 5
Now, consumer’s surplus
CS = \(\int_0^{q_e}\) D(q) dq – p_eq_e
= \(\int_0^3 \frac{20}{q+1}\) dq – (5) (3)
= 20 ln (q + 1)\(\left.\right|_0 ^3\) – 15
= 20 ln 4 – 15
= 20 × 2 log 2 – 15
= 40 (0.6932) – 15
= ≈ 12.73.

Question 30.
Surjeet purchased a new house, costing ₹ 40,00,000 and made a certain amount of down payment so that he can pay the balance by taking a home loan from XYZ Bank. If his equated monthly instalment is ₹ 30,000, at 9 % interest compounded monthly (reducing balance method) and payable for 25 years, then what is the initial down payment made by him? [Use (1.0075)^{– 300} = 0.1062]
Answer:
Purchase = ₹ 40,00,000
Down payment = ₹ x
Balance, P = ( 40,00,000 – x)
i = \(\frac{9}{1200}\)
n = 25 × 12
EMI = ₹ 30,000
Since,
EMI = \(\frac{P \times i \times(1+i)^n}{(1+i)^n-1}\)
⇒ 30000 = \(\frac{(4000000-x) \times 0.0075}{1-(1.0075)^{-300}}\)
⇒ 30000 = \(\frac{(4000000-x) \times 0.0075}{1-0.1062}\)
⇒ x = 424800
Down payment = ₹ 4,24,800.

Question 31.
The cost of a TV depreciates by ₹ 800 during the second year and by ₹ 700 during the third year. Calculate the rate of depreciation per annum. Also, find the original cost of machine.
Answer:
Let the original cost of the TV be ₹ P and the rate of depreciation be r % p.a.
Then the value of TV (in ₹) after 1 year, 2 years and 3 years are P(1 – i), P(1 – i)² and P(1 – j)³, respectively,
where i = \(\frac{r}{100}\)
According to question,
P(1 – i) – P(1 – i)² = 800
and P(1 – i)² – P(1 – i)³ = 700
⇒ P(1 – i) [1 – (1 – i)] = 800
and P(1 – i)² [1 – (1 – i)] = 700
⇒ P (1 – i) i = 800 ………………(i)
and P(1 – i)² i = 700 ……………..(ii)
On dividing eq. (ii) by eq. (i), we get
1 – i = \(\frac{700}{800}\)
⇒ 1 – i = \(\frac{7}{8}\)
⇒ i = 1 – \(\frac{7}{8}\)
⇒ i = \(\frac{1}{8}\)
∴ \(\frac{r}{100}=\frac{1}{8}\)
⇒ r = \(\frac{100}{8}\) = 12.5 %
Hence, the rate of depreciation = 12.5% p.a.
Putting i = \(\frac{1}{8}\) in eq. (i), we get
P (1 – \(\frac{1}{8}\)) × \(\frac{1}{8}\) = 800
⇒ P × \(\frac{7}{8 \times 8}\) = 800
⇒ P = \(\frac{800 \times 8 \times 8}{7}\)
= ₹ 7314.28
Hence, the original cost of TV is ₹ 7314.

Section – D
(This section comprises of long answer type questions (LA) of 5 marks each)

Question 32.
An unbiased coin is tossed 4 times. Find the mean and variance of number of heads obtained.
Answer:
Given, n = 4
Getting p = \(\frac{1}{2}\)
and q = \(\frac{1}{2}\)

Mean = Σxp(x)
= \(\frac{32}{16}\) = 2
Variance = Σ x² p(x) – {Σ xp(x)}²
= \(\frac{80}{16}\) – (2)²
= 5 – 4 = 1

OR

It is known that 3% of plastic buckets manufactured in a factory are defective, using the Poisson distribution on a sample of 100 buckets, find the probability of:
(i) Zero defective buckets
(ii) At most one bucket is defective [Use e^-3 = 0.049]
Answer:
Probability of defective bucket = 0.03
n = 100
m = np
= 100 × 0.03 = 3
Let X = number of defective buckets in a sample of 100
P(X = r) = \(\frac{m^r e^{-m}}{r !}\)
r = 0, 1, 2, 3, ……………

(i) P(no defective bucket) = P(r = 0)
= \(\frac{3^0 e^{-3}}{0 !}\)
= 0.049

(ii) P (at most one defective bucket) = P (r = 0, 1)
= \(\frac{3^0 e^{-3}}{0 !}+\frac{3^1 e^{-3}}{1 !}\)
= 0.049 + 0.147
= 0.196.

Question 33.
A company manufactures two types of products A and B. Each unit of A requires 3 gram of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 gram of chromium. The firm can produce 9 gram of nickel and 8 grams of chromium. The profit is ₹ 40 on each unit of product of type A and ₹ 50 on each unit of type B. How many units of each type should the company manufactures so as to earn maximum profit? Use linear programming to find the solution.
Answer:

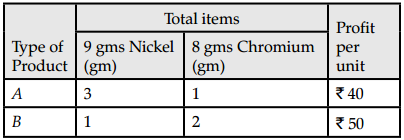
Let x = Number of units of type A
y = Number of units of type B
Maximize Z = 40x + 50y
Subject to the constraints,
3x + y ≤ 9
x + 2y ≤ 8
and x ≥ 0, y ≥ 0
Consider the equation,
3x + y = 9

x	0	3	2
y	9	0	3

and x + 2y = 8

x	0	8	2
y	4	0	3

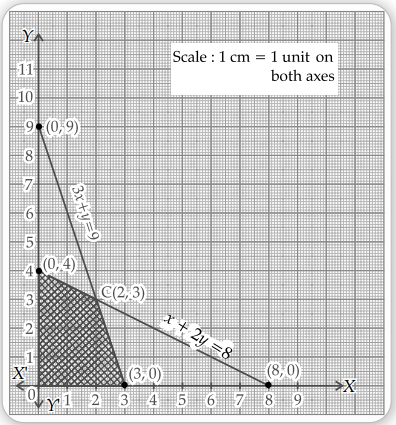
Shaded region in the diagram represents the feasible solution.
Now, we can determine the maximum value of Z by evaluating the value of Z at the four points (vertices) as shown below.

Vertices	Z = 40x + 50y
(0, 0)	Z = 40 × 0 + 50 × 0 = 0
(3, 0)	Z = 40 × 3 + 50 × 0 = ₹ 120
(0, 4)	Z = 40 × 0 + 50 × 4 = ₹ 200
(2, 3)	Z = 40 × 2 + 50 × 3 = ₹ 230

From graph,
Maximum profit, Z = 230
∴ Number of units of type A is 2 and number of units of type B is 3.

Question 34.
An event management company charges ₹ 4,800 per guest, for a bulk booking for 100 guests. In addition, it offers a discount of ₹ 200 for each group of 10 guests over and above 100 guest booking. What is the number of guests that will maximise the amount of money the company receives on a booking? What is the maximum profit on such booking?
Answer:
Let x be the number of guests for the booking
Clearly, x >100 to avail discount
∴ Profit, P = [4800 – \(\frac{20}{100}\) (x – 100)] x
= 6800x – 20x²
⇒ \(\frac{d P}{d x}\) = 6800 – 40x
⇒ x = 170
As \(\frac{d^2 P}{d x^2}\) = – 40 < 0, ∀ x
A booking for 170 guests will maximise the profit of the comapny and profit = ₹ 5,78,000

OR

A jet of enemy is flying along the curve y = x² + 2 and a soldier is placed at the point (3, 2). Find the minimum distance between the soldier and the jet.
Answer:
Let P(x, y) be the position of the jet and the soldier is placed at A (3, 2).
⇒ AP =\(\) ……………(i)
As given, y = x² + 2
⇒ y – 2 = x²
∴ AP² = (x – 3)² + x⁴ = z (say)
∴ \(\frac{d z}{d x}\) = 2 (x – 3) + 4x³
For maximum and minimum value,
\(\frac{d z}{d x}\) = 0
∴ 2x – 6 + 4x³ = 0
Putx = 1
2 – 6 + 4 = 0
∴ x – 1 is a factor
and \(\frac{d^2 z}{d x^2}\) = 12x² + 2
Now, \(\frac{d^2 z}{d x^2}\) (at x = 1) > 0
∴ z is minimum,when x = 1, y = 1 + 2 = 3 [from (ii)]
∴ Minimum distance = \(\left|\sqrt{(1-3)^2+(3-2)^2}\right|\)
= √5 units [from (ii)]

Question 25.
Use product \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
0 & 2 & -3 \\
3 & -2 & 4
\end{array}\right]\left[\begin{array}{ccc}
-2 & 0 & 1 \\
9 & 2 & -3 \\
6 & 1 & -2
\end{array}\right]\) to solve the system of equations x + 3z = 9, – x + 2y – 2z = 4, 2x – 3y + 4z = – 3.
Answer:
AB = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
0 & 2 & -3 \\
3 & -2 & 4
\end{array}\right]\left[\begin{array}{ccc}
-2 & 0 & 1 \\
9 & 2 & -3 \\
6 & 1 & -2
\end{array}\right]\)
= \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
AB = I
Or, A^-1 = B
= \(\left[\begin{array}{ccc}
-2 & 0 & 1 \\
9 & 2 & -3 \\
6 & 1 & -2
\end{array}\right]\)
Given equations in matrix form are:
\(\left[\begin{array}{ccc}
1 & -1 & 2 \\
0 & 2 & -3 \\
3 & -2 & 4
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{c}
9 \\
4 \\
-3
\end{array}\right]\)
AX = C
Or, X = (A)^-1C
= (A^-1)C
Or, \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{ccc}
-2 & 9 & 6 \\
0 & 2 & 1 \\
1 & -3 & -2
\end{array}\right]\left[\begin{array}{c}
9 \\
4 \\
-3
\end{array}\right]=\left[\begin{array}{l}
0 \\
5 \\
3
\end{array}\right]\)
Or, x = 0, y = 5, z = 3.

Section – E
(This section comprises of 3 source based questions (Case Studies) of 4 marks each)

CASE STUDY – 1

Question 36.
Read the following text and answer the following questions on the basis of the same:

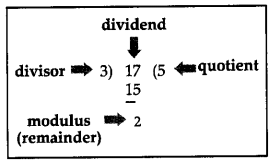
Modular arithmetic was introduced by Carl Friedrich Gauss on the very first page of his magnum opus Arithmetical Investigations, or Disquisitiones Arithmeticae. Modular arithmetic is a system of arithmetic for integers, which considers the remainder. The modulus is another name for the remainder after division. For example, 17 mod 3 = 2, since if we divide 17 by 3, we get 5 with remainder 2. Remainder is simply the remaining part after the arithmetic division between two integer number whereas Modulus is the sum of remainder and divisor when they are oppositely signed and remaining part after the arithmetic division when remainder and divisor both are of same sign.

(a) What is remainder when 220 + 330 + 440 + 550 + 117 is divided by 7?
Answer:
Consider, 2^7-1 ≡ 1(mod 7)
⇒ 2⁶ ≡ 1(mod 7)
⇒ (2⁶)³ ≡ 1(mod 7)
⇒ 2¹⁸ ≡ 1(mod 7)
Multiply throughout by 2², we get
⇒ 2¹⁸ . 2² ≡ 2²(mod 7)
⇒ 2²⁰ ≡ 4(mod 7) ……………(i)
Similarly, 3^7-1 ≡ 1(mod 7)
⇒ 3⁶ ≡ 1(mod 7)
⇒ (3⁶)⁵ ≡ 1(mod 7)
⇒ 3³⁰ ≡ 1 (mod 7) ………….(ii)
and 4^7-1 ≡ 1 (mod 7)
⇒ 4⁶ ≡ 1 (mod 7)
(4⁶)⁶ ≡ 1 (mod 7)
⇒ 4³⁶ ≡ 1 (mod 7)
Multiply throughout by 4⁴, we get
⇒ 4³⁶ 4⁴ 4⁴ (mod 7)
⇒ 4⁴⁰ 256 (mod 7)
⇒ 4⁴⁰ ≡ 4 (mod 7) …….(m) 1
Next consider, 5^7-1 ≡ 1 (mod 7)
⇒ 5⁶ ≡ 1(mod 7)
⇒ (5⁶)⁸ ≡ 1 (mod 7)
⇒ 5⁴⁸ ≡ 1 (mod 7)
Multiply throughout by 5², we get
⇒ 5⁴⁸ 5² ≡ 5² (mod 7)
⇒ 5⁵⁰ = 25 (mod 7)
⇒ 5⁵⁰ ≡ 4 (mod 7) …………..(iv)
Finally consider,
⇒ 11^7-1 ≡ 1 (mod 7)
⇒ 11⁶ ≡ 1 (mod 7)
Multiply throughout by 11, we get
⇒ 11⁶ . 11 ≡ 11(mod7)
⇒ 11⁷ ≡ 11 (mod 7)
⇒ 11⁷ ≡ 4 (mod 7)
Now adding (i), (ii), (iii), (iv) and (v), we get
2²⁰ + 3³⁰ + 4⁴⁰ + 5⁵⁰ + 11⁷ ≡ (4 + 1 + 4 + 4 + 4) (mod 7)
⇒ 2²⁰ + 3³⁰ + 4⁴⁰ + 5⁵⁰ + 11⁷ ≡ 17 (mod 7)
⇒ 2²⁰ + 3³⁰ + 4⁴⁰ + 5⁵⁰ + 11⁷ ≡ 3 (mod 7)

OR

(b) Mayank has 44 boxes of soda in his truck. The cans of soda in each box are packed oddly so that there are 113 cans of soda in each box. Mayank plans to pack the sodas into cases of 12 cans to sell. After making as many complete cases as possible, how many sodas will Mayank have leftover?
Answer:
Here, we have to find the remainder of product 44.
113 when divided by 12.
So, 44 = 3.12 + 8
113 = 9.12 + 5
Therefore, 44.113 = (3.12 + 8) (9.12 + 5)
= (3.9).12² + (3.5 + 8.9).12 + (8.5)
Here, each part of the product is a multiple of 12, except the product of the remainders when each 44 and 113 are divided by 12.
That part of the product is 8.5 = 40, which leaves a remainder of 4 when divided by 12.
So, Mayank has 4 sodas leftover after making as many cases of 12 as possible.

CASE STUDY – II

Question 37.
Read the following text and answer the following questions on the basis of the same:

In regards to product warranties, manufacturer defines the life span of a product to be the length of time that a product is in production and/or has parts in supply to support the repair or replacement of that product. The life span of certain kinds of electronic devices have mean of 300 hours and standard derivation of 25 hours. Assuming that the distribution of these life spans, which are measured to the nearest hour, can be approximated closely with a normal curve.

(i) Write the formula for Normal distribution.
Answer:
(i) The probability density function of Normal or Gaussian distribution is given by;
f(x, μ, σ) = \(\frac{1}{\sigma \sqrt{2 \pi}} e^{\frac{-(x-\mu)^2}{2 \sigma^2}}\)
where
x is the variable
μ is the mean
σ is the stndard deviation

(ii) Write the value of constant ‘e’ appearing in Normal Distribution.
Answer:
The value of constant ‘e’ appearing in Normal Distribution is 2.7183.
This is a standard constant.

(iii) Find the probability that any one of these electronic devices will have a life span of more than 350 hours. [Given P(0 ≤ Z ≤ 2) = 0.4772]
Answer:
Let X denotes the life spans of the given electronic devices.
Then X is normally distributed with mean, μ = 300 and standard deviation, σ = 25
Let Z be the standard normal variate.
Then
Z = \(\frac{X-\mu}{\sigma}\)
Z = \(\frac{X-300}{25}\)
when X = 350, we get
Z = \(\frac{350-300}{25}\)
= \(\frac{50}{25}\) = 2
∴ P(X > 350) = P(Z > 2)
= 0.5 – P(0 ≤ Z ≤ 2)
= 0.5 – 0.4772
= 0.0228

OR

What percentage will have life spans from 220 to 260 hours. [Given P(0 ≤ Z ≤ 3.2) = 0.4993 and P(0 ≤ Z ≤ 1.6) = 0.4452].
Answer:
When X = 220, we get
Z = \(\frac{220-300}{25}\) = 3.2
and when X = 260, we get
Z = \(\frac{260-300}{25}\) = – 1.6
∴ P(220 ≤ X ≤ 260) = P(- 3.2 ≤ Z ≤ – 1.6)
= P(1.6 ≤ Z ≤ 3.2)
= P (0 ≤ Z ≤ 3.2) – P(0 ≤ Z ≤ 1.6)
= 0.4993 – 0.4452
= 0.0541 1
Thus, 5.41% of the electronic devices will have life spans from 220 to 260.

CASE STUDY – III

Question 38.
Read the following text and answer the following questions on the basis of the same:

Today in class Mr. Agarwal is teaching the Method of Least Squares to measure the trend in time series. After explaining the method, he had taken an example which is as follows:

Given below are the data relating to the sales of a product in a district.
Fit a straight line trend by the method of least squares and tabulate the trend values.

To solve the given example, he constructed the following table:
Computation of trend values by the method of least squares.

Year (t)	Sales (y)	x=\(\frac{(t – 2018.5)}{0.5}\)	xy	x2
2015	6.7	– 7	– 46.9	49
2016	5.3	– 5	– 26.5	25
2017	4.3	– 3	– 12.9	9
2018	6.1	– 1	– 6.1	1
2019	5.6	1	5.6	1
2020	7.9	3	23.7	9
2021	5.8	5	29.0	25
2022	6.1	7	42.7	49

Here, n = 8 (even)
So, origin is mean of two middle years
i.e., \(\frac{2018+2019}{2}\) = 2018.5

(i) Write the general equation of straight line trend.
Answer:
Equation of the straight line trend is given by
Y = a + bX

(ii) Find trend equation for the given situation.
Answer:
Σy = 6.7 + 5.3 + 4.3 + 6.1 + 5.6 + 7.9 + 5.8 + 6.1
a = \(\frac{\Sigma y}{n}\)
Here, n = 8 and Σy = 47.8
So, a = \(\frac{47.8}{8}\)
= 5.975
Σxy = – 46.9 – 26.5 – 12.9 – 6.1 + 5.6 + 23.7 + 29.0 = 8.6
Here, n = 7 and Σxy = 8.6 and Σx² = 168
So, b = \(\frac{8.6}{168}\)
= 0.051
Thus, trend equation is given by y_t = 5.975 + 0.051 x

(iii) Find the trend value for year 2015.
Answer:
For year 2015,
x = – 7
∴ y_t = 5.975 + 0.051 (- 7)
= 5.618

OR

Find the trend value for year 2016.
Answer:
For year 2016,
x = – 5
∴ y_t = 5.975 + 0.051 (- 5)
= 5.975 – 0.255
= 5.720