CBSE Sample Papers for Class 11 Physics Set 4 with Solutions

Students can access the CBSE Sample Papers for Class 11 Physics with Solutions and marking scheme Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Physics Set 4 with Solutions

Time Allowed : 3 hours
Maximum Marks : 70

General Instructions:

1. There are 33 questions in all. All questions are compulsory.
2. This question paper has five sections: Section A, Section B, Section C, Section D and Section E.
3. All the sections are compulsory.
4. Section A contains sixteen questions, twelve MCQ and four Assertion Reasoning based of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study based questions of four marks each and Section E contains three long answer questions of five marks each.
5. There is no overall choice. However, an internal choice has been provided in one question in Section B, one question in Section C, one question in each CBQ in Section D and all three questions in Section E. You have to attempt only one of the choices in such questions
6. Use of calculators is not allowed.
7. You may use the following values of physical constants where ever necessary

• c = 3 × 10⁸ m/s
• me = 9.1 × 10^-31 kg
• µ₀ = 4π × 10^-7 TmA^-1
• ε₀ = 8.854 × 10^-12 × C² N^-1 m^-2
• Avogadro’s number = 6.023 × 10²³ per gram mole

Section – A

Question 1.
The pair of the quantities having same dimensions is
(A) Displacement, velocity
(B) Time, frequency
(C) Wavelength, focal length
(D) Force, acceleration
Answer:
(C) Wavelength, focal length

Explanation:
Both has the dimension of length.

Question 2.
Which of the following remains constant if a body travels with constant acceleration?
(A) Time
(B) Velodty
(C) Displacement
(D) None of these
Answer:
(D) None of these

Explanation:
Acceleration remains constant. So velocity, time and displacement change.

Question 3.
A stone of mass m is tied to a string of length l and rotated in a circle with a constant speed v . If the string is released, the stone flies
(A) radially outward
(B) radially inward
(C) tangentially outward
(D) in any arbitrary direction
Answer:
(C) tangentially outward

Explanation:
In circular motion, the direction of velocity at any point is tangent to the circle.

Question 4.
Angle between equal vectors is
(A) 0°
(B) 30°
(C) 90°
(D) 180°
Answer:
(A) 0°

Explanation:
The equal vectors lie on the same line, are directed in the same direction, and have the same length. So, the angle between them is 0.

Question 5.
The proper use of lubricants cannot reduce
(A) Static friction
(B) Inertia
(C) Sliding friction
(D) Rolling friction
Answer:
(B) Inertia

Explanation:
Lubricant can reduce friction. It cannot reduce the inertia. Inertia is related to mass.

Question 6.
What is the radius of gyration of a uniform rod whose length is L and passes through the centre of mass
(A) \(\frac{L}{\sqrt{3}}\)
(B) \(\frac{L}{\sqrt{2}}\)
(C) \(\frac{L}{2 \sqrt{3}}\)
(D) \(\frac{L}{3 \sqrt{2}}\)
Answer:
(C) \(\frac{L}{2 \sqrt{3}}\)

Explanation:
Moment of inertia of the rod = I = \(\frac{\mathrm{ML}^2}{12}\)
If the radius of gyration about the same axis be k, then
I = Mk²
∴ Mk² = \(\frac{M L^2}{12}\)
or, k² = \(\frac{L^2}{12}\)
∴ k = \(\frac{L}{2 \sqrt{3}}\)

Question 7.
In the following stress strain graph the yield point is 1000 ~

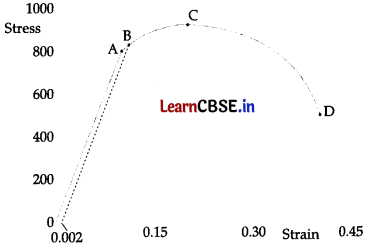
(A) A
(B) B
(C) C
(D) D
Answer:
(B) B

Question 8.
Water in a capillary tube rises to a height 6 cm. The area of cross section of the capillary is made one- fourth. Water will raise upto
(A) 6 cm
(B) 12 cm
(C) 3 cm
(D) 24 cm
Answer:
(B) 12 cm

Explanation:
Rise of liquid in capillary (h) ∝ \(\frac{1}{\sqrt{\text { Area of cross-section }}}\)
Or, \(\frac{h_1}{h_2}=\frac{\sqrt{A_2}}{\sqrt{A_1}}\)
Or, \(\frac{6}{h_2}=\frac{1}{\sqrt{4}}\)
Or, \(\frac{6}{h_2}=\frac{1}{2}\)
∴ h₂ = 12 cm

Question 9.
Two ends of a metal rod are maintained at temperatures 200°C and 210°C. The rate of heat flow was found to be 10 J/s. If the ends of the rod are maintained at 400°C and 410°C/ the rate of heat flow will be
(A) 10 J/s
(B) 20 J/s
(C) 80 J/s
(D) 30 J/s
Answer:
(A) 10 J/s

Explanation:
\(\frac{\Delta Q}{\Delta t}=k A \frac{\Delta T}{\Delta x}\)
As the length of the rod and temperature difference remain constant, the rate of heat flow remains constant.

Question 10.
Two pipes each 20 cm long – one is closed at one end and the other is open at both ends are excited by a frequency 425 Hz. Which one will be in resonance if the speed of sound in air is 340 ms^-1 ?
(A) One end closed pipe
(B) Both end open pipe
(C) Both of the pipes
(D) None of the pipes
Answer:
(A) One end closed pipe

Explanation:
For closed pipe, fundamental frequency,
υ = \(\frac{v}{4 l}\)
= \(\frac{340}{4 \times 0.2}\)
= 425 Hz.
So, there will be resonance.
For both end open pipe, fundamental frequency
υ = \(\frac{v}{2 l}\)
= \(\frac{340}{2 \times 0.2}\)
= 850 Hz
Then, there will be no resonance.

Question 11.
At what temperatures will the speed of sound in air be 3 times its value at 0° C?
(A) 2457°C
(B) 2184°C
(C) 2184 K
(D) None of the above
Answer:
(B) 2184°C

Explanation:
υ ∝ √T
or, \(\frac{3 v_0}{v_0}=\sqrt{\frac{T}{273+0}}\)
For given condition,
υ_t = 3υ₀
∴ \(\frac{3 v_0}{v_0}=\sqrt{\frac{T}{273+0}}\)
or, √T = 3 \(\sqrt{273}\)
T = 9 × 273 = 2457 K
T = (2457 – 273)° C
T = 2184°C

Question 12.
The displacement of a particle is represented by the equation y = sin3 cot. The motion is
(A) non – periodic.
(B) periodic but not simple harmonic.
(C) simple harmonic with period \(\frac{2 \pi}{\omega}\)
(D) simple harmonic with period \(\frac{\pi}{\omega}\)
Answer:
(B) periodic but not simple harmonic.

Explanation:
as \(\frac{d^2 y}{d t^2}\) is not ∝ (- y)
∴ It is not SI-1M but it is a periodic motion with period \(\frac{2 \pi}{\omega}\).

For Questions 13 to 16 two statements are given – one labelled Assertion (A) and other labelled Reason (R). Select the correct answer to these questions from the options as given below.
(A) If both Assertion and Reason are true and Reason is correct explanation of Assertion.
(B) If both Assertion and Reason are true and Reason is not the correct explanation of Assertion.
(C) If Assertion is true but Reason is false.
(D) If both Assertion and Reason are false.

Question 13.
Assertion (A) : In y = A sin (ωt – kx), (ωt – kx) is dimensionless.
Reason (R) : Because dimension of ω = [M⁰L⁰T⁰].
Answer:
(C) If Assertion is true but Reason is false.

Explanation:
Trigonometric functions are dimensionless. Hence, Sin θ is dimensionless.
So, ωt – kx is dimensionless. The assertion is true.
[ωt] = [M⁰L⁰T⁰]
Or, [ω][T] = [M⁰L⁰T⁰]
∴ [ω] = [M⁰L⁰T^-1]
So, the reason is false.

Question 14.
Assertion (A) : The dot product of one vector with another vector may be a scalar or a vector.
Reason (R) : If the product of two vectors is a vector quantity, then product is called a dot product.
Answer:
(D) If both Assertion and Reason are false.

Explanation:
The dot product of two vectors is always a scalar and the cross product of two vectors is always vector. So, both assertion and reason are false.

Question 15.
Assertion (A) : If momentum of a body increases by 50%, its kinetic energy will increase by 125%.
Reason (R) : Kinetic energy is proportional to square of velocity.
Answer:
(A) If both Assertion and Reason are true and Reason is correct explanation of Assertion.

Explanation:
Kinetic energy = E = \(\frac{p^2}{2 m}\)
Where p = momentum = mv
Momentum increases by 50%.
So, Increased momentum = P’ = 1.5P
Increased kinetic energy = E’ = \(\frac{1.5 P^2}{2 m}\) = 2.25E
Increase in kinetic energy = 2.25E – E = 1.25 E i.e. 125%
So, the assertion is true.
Kinetic energy = \(\frac{p^2}{2 m}\) = \(\frac{1}{2}\) mv²
∴ Kinetic energy ∝ v²
So, the reason is also true and it explains the assertion.

Question 16.
Assertion (A) : Any two objects in the universe attract each other by a force called gravitation force.
Reason (R) : The force of gravitation exerted by the earth is called gravity.
Answer:
(B) If both Assertion and Reason are true and Reason is not the correct explanation of Assertion.

Section – B

Question 17.
(i) What type of mechanical waves do you expect to exist in
(a) vacuum,
(b) air,
(c) inside the water,
(d) rock
(e) on the surface of water ?
Answer:
(a) No wave,
(b) longitudinal waves,
(c) longitudinal waves,
(d) transverse or longitudinal or both (separately),
(e) combined longitudinal and transverse (ripples).

(ii) What is the phase difference between the waves y = a cos (ωt + kx), and y = a sin(ωt – kx) ?
Answer:
Phase difference = \(\frac{\grave{A}}{2}\) = 90°.

Question 18.
(a)Where will a person hear maximum sound, at node or antinode ?
Answer:
Perception of sound is due to pressure variations which is maximum at nodes.

(b)What is the distance between a node and an adjoining antinode in a stationary wave ?
Answer:
It is one quarter of the wavelength (i.e., \(\frac{\lambda}{4}\)).

Question 19.
(a) How does the M.I. change with speed of rotation ?
Answer:
M.I. is not affected by speed of rotation of the body.

(b) The moment of inertia of two rotating bodies A and B are fA and JB (7A>/B) and their angular momenta are equal. Which one has greater Kinetic Energy ?
Answer:
∵ K = \(\frac{L^2}{2 I}\)
or K ∝ < \(\frac{1}{1}\)
∴ K_B > K_A

Question 20.
Under what conditions does the equality \(|\vec{A}+\vec{B}|=|\vec{A}-\vec{B}|\) hold good ?
Answer:
\(|\vec{A}+\vec{B}|=\sqrt{A^2+B^2+2 A B \cos \theta}\)
\(|\overline{\mathrm{A}}-\overline{\mathrm{B}}|=\sqrt{A^2+B^2-2 A B \cos \theta}\)
So, \(|\bar{A}+\bar{B}|\) will be equal to \(|\bar{A}-\bar{B}|\) only when
2AB cos θ = – 2AB cos θ
Or, 4 AB cos θ = 0
So, either AB = 0 or cos θ = 0
AB = 0 is not possible since both A and B are non zero.
So, cos θ = 0, i.e, θ = 90°
So, \(\vec{A}\) and \(\vec{B}\) are perpendicular to each other, then \(|\bar{A}+\bar{B}|\) = \(|\bar{A}-\bar{B}|\)

Question 21.
Mention four pair physical quantities having same dimensional formulae but different units.
Answer:
(a) (i) Linear momentum [MLT^-1] kg ms^-1
(ii) Impulse [MLT^-1] Ns

(b) (i) Work and energy [ML²T^-2] J
(ii) Torque [ML²T^-2] Nm

(c) (j) Surface tension [ML⁰T^-2] Nm^-1
(ii) Surface energy [ML⁰T^-2] Jm^-2

(d) (i) Angular velocity [M⁰L⁰T^-1] rad s^-1
(ii) Velocity gradient [M⁰L⁰T^-1] s^-1
(iii) Frequency [M⁰L⁰T^-1] Hz

OR

Suggest a physical situation for the following graph.

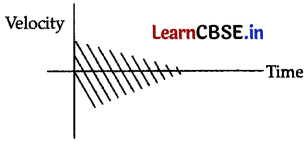
Answer:
Suitable physical situation:
A ball is thrown up with some initial velocity. It is rebounding from the floor with reduced speed after each hit.

Section – C

Question 22.
A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 s, what is the magnitude and direction of acceleration of the stone?
Answer:
Lengthofstring= r = 80 cm = 0.8 m
Number of revolutions = 14
Time taken = 25 s
Frequency = υ = \(\frac{14}{25}\) Hz
Angular frequency = ω = 2πυ
= 2 × \(\frac{22}{7}\) × \(\frac{14}{25}\)
= \(\frac{88}{25}\) rad s^-1
Centripetal acceleration = ω²r
= \(\left(\frac{88}{25}\right)^2\) × 0.8
= 9.91 m/s²
Direction is along the string, towards the centre.

Question 23.
(i) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?
Answer:
Gravitational force is a conservative force. Since the work done by a conservative force over a closed path is zero, the work done by the gravitational force over every complete orbit of a comet is zero.

(ii) An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Then why does its speed increase progressively as it comes closer and closer to the earth?
Answer:
When an artificial satellite, orbiting around earth, moves closer to earth, its potential energy decreases because of the reduction in the height. Since the total energy of the system remains constant, the reduction in PE. results in an increase in K.E. Hence, the velocity of the satellite increases. However, due to atmospheric friction, the total energy of the satellite decreases by a small amount.

Question 24.
A steel wire of length 4.7 m and cross-sectional area 3.0 × 10^-5 m² stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0 × 10^-5 m² under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
Answer:
Change in length = ∆L_copper = ∆L_steel = ∆L
Applied force = F
Young’s Modulus of steel wire = γ_steel
= \(\frac{F}{A_{\text {steel }}} \times \frac{L_{\text {steel }}}{\Delta L}\)
= \(\frac{F}{3 \times 10^{-5}} \times \frac{4.7}{\Delta L}\)
Young’s Modulus of copper wire = γ_copper
= \(\frac{F}{A_{\text {copper }}} \times \frac{L_{\text {copper }}}{\Delta L}\)
= \(\frac{F}{4 \times 10^{-5}} \times \frac{3.5}{\Delta L}\)
The required ratio = \(\frac{Y_{\text {steel }}}{Y_{\text {copper }}}\)
= \(\frac{4.7 \times 4 \times 10^{-5}}{3.5 \times 3 \times 10^{-5}}\)
= 1.79 : 1

Question 25.
A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0 cm of water in one arm and 12.5 cm of spirit in the other. What is the specific gravity of spirit?
Answer:

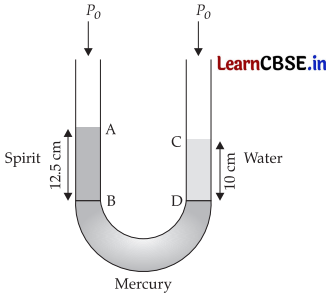
Height of spirit column = h₁ = 12.5 cm
Height of water column = h₂ = 10 cm
P₀ = Atmospheric pressure
ρ₁ = Density of spirit
ρ₂ = Density of water
Pressure at B = P₀ + h₁ρ₁g
Pressure at D = P₀ + h₂ρ₂g
Pressures at B and D are same.
So, P₀ + h₁ρ₁g = P₀ + h₂ρ₂g
Or, h₁ρ₁ = h₂ρ₂
Or, \(\frac{\rho_1}{\rho_2}=\frac{h_2}{h_1}\)
Or, \(\frac{\rho_1}{\rho_2}=\frac{10}{12.5}\)
Or, \(\frac{\rho}{\rho}\) = 0.8
∴ Specific gravity of spirit = 0.8.

Question 26.
A hole is drilled in a copper sheet. The diameter of the hole is 4.24 cm at 27.0 °C. What is the change in the diameter of the hole when the sheet is heated to 227 °C? Coefficient of linear expansion of copper = 1.70 × 10^-5K^-1.
Answer:
\(\frac{\text { Change in area }}{\text { Original area }}\) = Coefficient of area expansion × Change in temperature
Or, \(\frac{\frac{\pi d_2^2}{4}-\frac{\pi d_1^2}{4}}{\frac{\pi d_1^2}{4}}\) = 2 × Coefficient of linear expansion × (T₂ – T₂)
Or, \(\frac{d_2^2-d_1^2}{d_1^2}\) = 2 × 1.7 × 10^-5 × (227 – 27)
Or, \(\frac{d}{d}\) – 1 = 2 × 1.7 × 10^-5 × 200
Or, \(\frac{d_2^2}{(4.24)^2}\) = 1 + 2 × 1.7 × 10^-5 × 200
Or, d₂² = 18.1
∴ d₂ = 4.2544 cm
So, change in diameter = 4.2544 – 4.24 = 0.0144 cm

Question 27.
(a) Why two bodies at different temperatures T₁ and T₂ when brought in thermal contact do not necessarily settle to the mean temperature \(\frac{T_1+T_2}{2}\) ?
Answer:
When two bodies at different temperatures are brought in thermal contact heat flows from the body at the higher temperature to the body at the lower temperature till equilibrium is achieved, i.e., the temperatures of both the bodies become equal. If the thermal capacities of both the bodies are equal then only the equilibrium temperature is equal to the mean temperature \(\frac{T_1+T_2}{2}\).

(b) Why the coolant used in a chemical or a nuclear plant (i.e., the liquid used to prevent the different parts of a plant from getting too hot) should have high specific heat?
Answer:
The coolant in a chemical or nuclear plant should have a high specific heat. This is because higher the specific heat of the coolant, higher is its heat absorbing capacity and vice versa. Hence, a liquid having a high specific heat absorbs more heat and hence is better coolant.

Question 28.
Which of the following examples represent periodic motion? Explain.
(a) A swimmer completing one (return) trip from one bank of a river to the other and back.
(b) A freely suspended bar magnet displaced from its N-S direction and released.
(c) An arrow released from a bow.
Answer:
(a) The swimmer’s motion is not periodic. The motion of swimmer between the banks of a river is to and forth. It does not have a definite period since the time taken by the swimmer during his back and forth journey may not be equal.

(b) The motion of a freely suspended magnet when displaced from its N-S direction and released is periodic. This is because the magnet oscillates about its equilibrium position with a definite period.

(c) Arrow release from a bow moves only in forward direction. It does not come backward. Hence, this motion is not periodic.

OR

A steel rod 100 cm long, clamped at two ends, is plucked at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
Answer:
Length of the rod = l = 100 cm = 1 m
Fundamental frequency = υ = 2.53 kHz
= 2.53 × 10³ Hz
When the rod is plucked at the middle, the nodes are formed at the two ends.

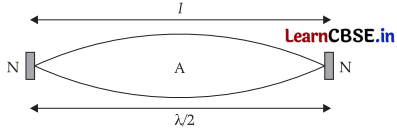
Distance between the two nodes = \(\frac{\lambda}{2}\)
In this case l = \(\frac{\lambda}{2}\)
∴ λ = 2l = 2 m
Speed of sound = υ = vλ
Or, υ = 2.53 × 10³ × 2
∴ υ = 5060 m/s

Section – D

Question 29.
Read the following text and answer the following questions on the basis of the same:

Clockwork refers to the inner workings of mechanical clock or watch (where it is known as “movement”) and different types of toys which work using a series of gears driven by a spring.

3

Clockwork device is completely mechanical and its essential parts are:

• A key (or crown) which you wind to add energy
• A spiral spring in which the energy is stored
• A set of gears through which the spring’s energy is released. The gears control how quickly (or slowly) a clockwork machine can do things. Such as in mechanical clock / watch the mechanism is the set of hands that sweep around the dial to tell the time. In a clockwork car toy, the gears drive the wheels.

Winding the clockwork with the key means tightening a sturdy metal spring, called the mainspring. It is the process of storing potential energy. Clockwork springs are usually twists of thick steel, so tightening them (forcing the spring to occupy a much smaller space) is actually quite hard work. With each turn of the key, fingers do work and potential energy is stored in the spring. The amount of energy stored depends on the size and tension of the spring. Harder a spring is to turn and longer it is wound, the more energy it stores.

While the spring uncoils, the potential energy is converted into kinetic energy through gears, cams, cranks and shafts which allow wheels to move faster or slower. In an ancient clock, gears transform the speed of a rotating , shaft so that it drives the second hand at one speed, the minute hand at 1/60 of that speed, and the hour hand at 1/3600 of that speed. Clockwork toy cars often use gears to make themselves race along at surprising speed.

(i) What is the meaning of “movement” of old age mechanical clocks?
(A) The gears which move the hands of the clock
(B) A spring and combination of gears which move the hands of the clock
(C) The hands of the clock
(D) The pendulum of the clock
Answer:
(B) A spring and combination of gears which move the hands of the clock

Explanation:
Movement refers to the inner workings of mechanical clock using a series of gears driven by a spring.

(ii) What type of energy is stored in the spring while winding it?
(A) Kinetic
(B) Potential
(C) Both (A) and (B)
(D) Heat
Answer:
(B) Potential

Explanation:
Winding the spring means tightening a sturdy metal spring. Ills the process of storing potential energy (forcing the spring to occupy a much smaller space) is actually quite hard work. With each turn of the key, fingers do work and potential energy is stored in the spring.

(iii) When the spring of a clockwork uncoils
(A) Kinetic energy is converted into potential energy
(B) Potential energy is converted into kinetic energy
(C) Potential energy is converted into heat, light and sound energy
(D) Kinetic energy is converted into heat, light and sound energy
Answer:
(B) Potential energy is converted into kinetic energy

Explanation:
When the spring uncoils, the potential energy is converted into kinetic energy through gears, cams, cranks and shafts which allow wheels to move faster or slower.

OR

In clockwork devices, ……………. transform the speed of a rotating ………………. to drive wheels slower or faster.
(A) Gear, shaft
(B) Shaft, gear
(C) Spring, gear
(D) Shaft, spring
Answer:
(A) Gear, shaft

Explanation:
In an ancient clock, gears transform the speed of a rotating shaft so that it drives the second hand at one speed, the minute hand at \(\frac{1}{60}\) of that speed, and the hour hand at \(\frac{1}{3660}\) of that speed. Clockwork toy cars often use gears to make themselves race along at surprising speed.

(iv) More energy is stored in a spring if the
(A) Spring is larger, harder and wound for a shorter time
(B) Spring is smaller, harder and wound for a shorter time
(C) Spring is larger, harder and wound for a longer time
(D) Spring is larger, softer and wound for a shorter time
Answer:
(C) Spring is larger, harder and wound for a longer time

Explanation:
With each turn of the key, fingers do work and potential energy is stored in the spring. The amount of energy stored depends on the size and tension of the spring. Harder a spring is to turn and longer it is wound, the more energy it stores.

Question 30.
Read the following text and answer any 4 of the following questions on the basis of the same:

Large distances such as the distance of a planet or a star from the earth cannot be measured directly with a metre scale. An important method in such cases is the parallax method.

When you hold a pencil in front of you against some specific point on the background (a wall) and look at the pencil first through your left eye A (closing the right eye) and then look at the pencil through your right eye B (closing the left eye), you would notice that the position of the pencil seems to change with respect to the point on the wall. This is called parallax. The distance between the two points of observation is called the basis. In this example, the basis is the distance between the eyes.

To measure the distance D of a far away planet S by the parallax method, we observe it from two different positions (observatories) A and B on the Earth, separated by distance AB = b at the same time as shown in Fig. We measure the angle between the two directions along which the planet is viewed at these two points. The ∠ASB in figure represented by symbol θ is called the parallax angle or parallactic angle.

As the planet is very far away, \(\frac{b}{D}\)< < 1 and therefore, θ is very small. Then we approximately take AB as an arc of length b of a circle with centre at S and the distance D as the radius AS = BS so that AB = b = Dθ where θ is in radians, then

(i) In parallax method the distance between two observation points is called
(A) Base
(B) Basis
(C) Distance
(D) Basic
Answer:
(B) Basis

Explanation:
The distance between the two observatories is the “basis”.

(ii) A star at a distance 8 × 10⁸ km is being observed from Vainu Bappu Observatory, Kavalur and ARIES Observatory, Nainital. The distance between the observatories is 2500 km. What is the “basis” of this measurement?
(A) 2500 km
(B) 1250 km
(C) 5000 km
(D) Data is insufficient to calculate
Answer:
(A) 2500 km

(iii) A star at a distance 2.5 × 10⁸ km is being observed from Vainu Bappu Observatory, Kavalur and ARIES Observatory, Nainital. The distance between the observatories is 2500 km. What is the value of parallax angle?
(A) 625 × 10⁸ radian
(B) 10^-5 radian
(C) 10⁵ radian
(D) 10^-5 degree
Answer:
(B) 10^-5 radian

Explanation:
b = D θ
b = 2500 km, D = 2.5 × 10⁸ = 10⁸ km
So, θ = \(\frac{b}{D}\)
= \(\frac{2500}{2.5}\) × 10⁸
= 10^-5 radian

(iv) Under which condition D = \(\frac{b}{\theta}\) relation is valid?
(D = Distance of star or planet from earth, θ = parallax angle, b = basis)
(A) \(\frac{b}{D}\) < < 1 (B) \(\frac{b}{D}\) > < 1
(C) \(\frac{D}{b}\) < < 1
(D) \(\frac{D}{b}\) = 1
Answer:
(A) \(\frac{b}{D}\) < < 1

Or

When you hold an ice-cream cone in front of you against some specific point on the background (a wall) and look at it first through your left eye (closing the right eye), it seems to be at position B. Now if you look at it through your right eye (closing the left eye), you will notice that now it is at position A.
What is the “basis” of this observation?
(A) AB
(B) LR
(C) (\frac{(L R+A B)}{2})
(D) LR + AB
Answer:
(B) LR

Section – E

Question 31.
(a) An artificial satellite is revolving around a planet of mass M and radius R, in a circular orbit of radius r. From Kepler’s third law about the period of a satellite around a common central body, square of the period of revolution T is proportional to the cube of the radius of the orbit r. Show using dimensional analysis, that T = \(\frac{K}{R} \sqrt{\frac{r^3}{g}}\) Where K is dimensionless constant and g is acceleration due to gravity.?
Answer:
Given From Kepler’s III law,
T ∝ r^3/2.
T is also function of g and R.
⇒ T ∝ r^3/2R_yg_x
= k^3/2R_yg_x
[k = dimension less constant of proportionality]
Substituting dimensionless in each term.
[L⁰M⁰T¹] = k [L^3/2 M⁰T⁰] [L¹M⁰T^-2] × [L]^y
K = [L^{x+y+\(\frac{3}{2}\)} T^{– 2x}]
For L, 0 = \(\frac{3}{2}\) + x + y
For T, 1 = 0 – 2x
⇒ x = – –
Therefore, 0 = \(\frac{3}{2}\) – \(\frac{1}{2}\) + y
y = – 1
Thus, T = kr^{\(\frac{3}{2}\)} g
R^-1 = \(\frac{k}{R} \sqrt{\frac{r^3}{g}}\)

(b) In the expression P = EL³ m^-5 G², Here, E, m, L and G denote energy, mass, angular momentum and gravitational constant, respectively, show that P is dimensionless qualntity.
Answer:
Since, E,L and G have dimensional formulas:
E = [ML²T^-2]
L = [ML²T^-1]
G = [L³M^-1-T^-2]
Hence, P = EL²m^-5G^-2 will have dimensions:
[P] = \(\frac{\left[M L^2 T^{-2}\right]\left[M^2 L^4 T^{-2}\right]}{\left[M^5\right]\left[L^0 M^{-2} T^{-4}\right]}\)
= M⁰L⁰T⁰
Thus, P is dimensionless quantity.

OR

(i) The velocity-displacement graph of a particle is shown in figure.

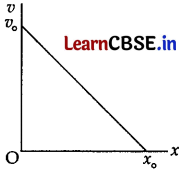
(a) Write the relation between v and x.
Answer:
Initial velocity = v₀
Let the distance travelled in time t = x₀
From graph,
tan θ = \(\frac{v_0}{x_0}=\frac{v_0-v}{x}\)

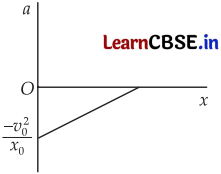
(b) Obtain the relation between acceleration and displacement and plot it.
Answer:

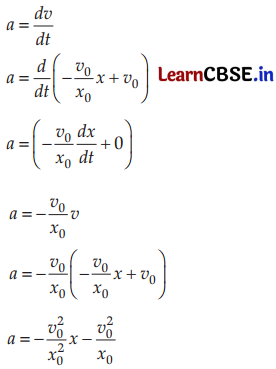
The variation of a with x is shown in the figure.
It is a straight line with a positive slope and a negative intercept.

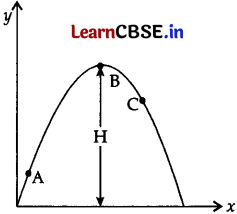
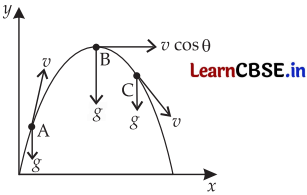
(ii) A particle is projected in air at some angle to the horizontal, moves along parabola as shown in Fig. where x and y indicate horizontal and vertical directions, respectively. As shown in the diagram, direction of velocity and acceleration at points A, B and C.

Answer:
Direction of the velocities at point A, B and C are along the tangent of the path at that point.
Acceleration at each point is the acceleration due to gravity vertically downwards.

Question 32.
(i) A body is being raised to a height h from the surface of Earth. What is work done (with sign) by
(a) applied force
(b) gravitational force?
Answer:
(a) Work done by applied force,
W_A = mgh cos 0° = mgh

(b) Work done by gravitational force
W_g = Force × displacement × cos θ
= mgh cos 180°
(∵ θ = 180°)
= – mgh

(ii) A bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in Fig. What will be the trajectory of the particle if the string is cut at

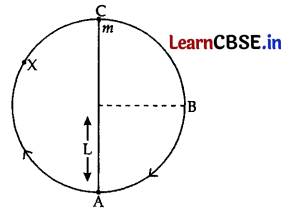
(a) point B?
(b) point C?
(c) point X?
Answer:
(a) If the string is cut at point B, the trajectory is straight line downward.
(b) At point C, parabolic path with vertex at C.
(c) At point X, it is parabolic path with vertex higher than X.

OR

Find the centre of mass of a uniform
(a) half-disc,
(b) quarter-disc.
Answer:
(a)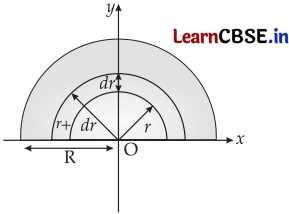

Let the mass of half disc be M.
Area of half disc = \(\frac{\pi R^2}{2}\)
Mass per unit area, m = \(\frac{2 M}{\pi R^2}\)

The half disc can be divided into a large number of semi-circular strips having mass dm, thickness dr, and radii varies from 0 → R
= \(\frac{\pi}{2}\) [(r + dr)² – r²]
= \(\frac{\pi}{2}\) [r² + dr² + 2rdr – r²]
Since, (dr²) is very small,
\(\frac{\pi}{2}\) (2r × dr) = πr dr
Mass of the strip, dm = πrdr × \(\frac{2 M}{\pi R^2}\)
= \(\frac{2 M}{R^2}\) . r dr
Let (x, y) be the coordinates of c. m. of this strip.
So, (x, y) = (0, \(\frac{2 r}{\pi}\))
Thus, x = 0, y = \(\frac{2 r}{\pi}\)
Let x cm and y cm be the co-ordinates of the centre of mass of semicircular strip.
Then

So, centre of mass of uniform half disc = (0, \(\frac{4 R}{3 \pi}\))

(b)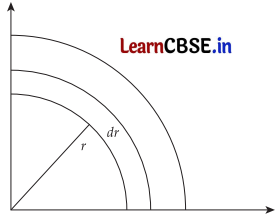

Mass per unit of quarter disc = \(\frac{M}{\frac{\pi R^2}{4}}\)
= \(\frac{4 M}{\pi R^2}\)
Using symmetry,
For half disc, y_cm = \(\frac{4 R}{3}\)
Similarly, for half disc, along x-axis centre of mass,
At x_cm = \(\frac{4 R}{3 \pi}\)
So, the centre of mass of quarter disc is \(\left(\frac{4 R}{3 \pi}, \frac{4 R}{3 \pi}\right)\).

Question 33.
(a) A steel rod (γ = 2.0 × 10¹¹ Nm^-2, and α = 10^{– 5} °C^-1) of length 1 m and area of cross-section 1 cm² is heated from 0° C to 200°C without being allowed to extend or bend. What is the tension produced in the rod?
Answer:
∆T = 200°C – 0°C = 200°C, α = 10^{– 5} °C^-1, l = 1 m
Area of cross-secfion, A = 1 cm² = 1 × 10^-4 m²
∴ \(\frac{\Delta l}{l}\) = α∆T
= 10^{– 5} × 200
= 2 × 10^{– 3}
Tension produced in steel rod = γA α∆T
= 2.0 × 10¹¹ × 1 × 10^-4 × 2 × 10^-3
= 4 × 10⁴ N

(b) If a drop of liquid breaks into smaller droplets, it results in lowering of temperature of the droplets. Let a drop of radius R, break into N small droplets each of radius r. Estimate the drop in temperature.
Answer:
When a big drop having radius R breaks into N droplets each of radius r, the volume remains constant.
∴ Volume of big drop = N × \(\frac{4}{3}\) πr³
Or, R³ = Nr³
or, N = \(\frac{R^3}{r^3}\)
Change in surface area = 4πR² – N⁴πr²
∆A = 4π (R² – Nr²)
Energy released = T × ∆A
= T × 4π (R² – Nr²)
Released energy lowers the temperature by ∆θ, then
Energy released = ms∆θ
T × 4π (R² – Nr²) = (\(\frac{4}{3}\) × R³ x ρ) s∆θ
[s = speccheat of liquid
ρ = density]
Or ∆θ = \(\frac{T \times 4 \pi\left(R^2-N r^2\right)}{\frac{4}{3} \pi R^3 \rho \times s}\)
= \(\frac{3 T}{\rho s}\left[\frac{R^2}{R^3}-\frac{N r^2}{R^3}\right]\)
∆θ = \(\frac{3 T}{\rho s}\left[\frac{1}{R}-\frac{1}{r}\right]\)
(∵ N = \(\frac{R^3}{r^3}\))

OR

(i) A rail track made of steel having length 10 m is clamped on a railway line at its two ends. On a summer day due to rise in temperature by 20° C, it is deformed as shown in figure. Find x (displacement of the centre) if α_steel = 1.2 × 10^-5/°C.

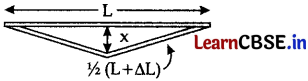
Answer:
Given α = 1.2 × 10^-5;°C^-1, L = 10 m, ∆T = 20°C
By Pythagoras theorem,
x² = [(\(\frac{L + ∆L}{2}\))² – (\(\frac{L}{2}\))²
= \(\frac{1}{4}\) [L² + ∆L² + 2L∆L] – \(\frac{L^2}{4}\)
x = – \(\sqrt{\Delta L+L \Delta L}\)
∆L² < < L, ∴ neglecting ∆L²
x = – × \(\sqrt{L \Delta L}\)
But ∆L = Lα∆t
∴ x = – \(\sqrt{L \times L \alpha \Delta t}\)
= – L \(\sqrt{\alpha \Delta t}\)
= \(\frac{10}{2} \times \sqrt{2 \times 1.2 \times 10^{-5} \times 20}\)
= 5 × \(\sqrt{4 \times 1.2 \times 10^{-4}}\)
= 5 × 2 × 1.1 × 10^-2
= 0.11 m
x = 11 cm

(ii) Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in Fig.

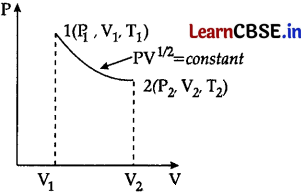
(a) Find the work done when the gas is taken from state 1 to state 2.
Answer:
Work done by the gas for process 1 to 2
∆W = \(\int_V^V\) PdV
= K \(\int_V^V \frac{d V}{\sqrt{V}}\)
= \(\left[\frac{\sqrt{V}}{-}\right]_V^V\)
= K (√V – √V)
= \(2 P_1 V_1^{\frac{1}{2}}\left[\sqrt{\mathrm{V}_2}-\sqrt{V_1}\right]\)

(b) What is the ratio of temperature T₁/T₂, if V₂ = 2V₁ ?
Answer:
From ideal gas equation-
PV = nRT

(c) Given the internal energy for one mole of gas at temperature T is (3/2) RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V₂ = 2V₁.
Answer:
Change in internal energy = U = \(\frac{3}{2}\) RT
∆U =U₂ – U₁
= \(\frac{3}{2}\) R (T₂ – T₁)
= \(\frac{3}{2}\) RT₁ (√2 – 1)
∆W = 2RT₁ (√2 – 1)
Such that,
∆Q = ∆U + ∆W
= \(\frac{3}{2}\) RT₁ (√2 – 1) + 2RT₁ (√2 – 1)
= (√2 – 1) RT₁ (\(\frac{3}{2}\) + 2)
Amount of heat supplied, ∆Q = \(\frac{7}{2}\) RT₁ (√2 – 1)