CBSE Sample Papers for Class 11 Applied Mathematics Set 5 with Solutions

Students can access the CBSE Sample Papers for Class 11 Applied Mathematics with Solutions and marking scheme Set 5 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Applied Mathematics Set 5 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

• This Question paper contains five sections A, B, C, D and E. Each section is compulsory. However, there is some internal choice in some questions.
• Section A has 18 MCQs and 2 Assertion Reason-based questions of 1 mark each.
• Section B has 5 Very Short Answer (VSA) questions of 2 marks each.
• Section C has 6 Short Answer (SA) questions of 3 marks each.
• Section D has 4 Long Answer (LA) questions of 5 marks each.
• Section E has 3 source-based/case-based/passage-based/integrated units of assessment (4 marks each) with subparts.
• Internal Choice is provided in 2 questions in Section B, 2 questions in Section C, 2 Questions in Section D. You have to attempt only one alternative in all such questions.

Section-A

(All Questions are compulsory. No internal choice is provided in this section)

Question 1.
\(\left\{\left(x^n\right)^{n-\frac{1}{n}}\right\}^{\frac{1}{n+1}}\) is equal to ________
(a) xⁿ
(b) x^n-1
(c) xⁿ⁺¹
(d) x²ⁿ
Answer:
Section-A
(b) x^n-1
Explanation:

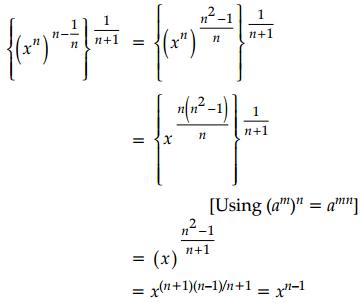
Question 2.
The value of log 0.0625 to the base 2 is
(a) 0
(b) 1
(c) -1
(d) -4
Answer:
(d) -4
Explanation:

Question 3.
If 8th Feb. 2005 was Tuesday, then the day of the week on 8th Feb 2004 was
(a) Tuesday
(b) Thursday
(c) Saturday
(d) Sunday
Answer:
(d) Sunday
Explanation:
The year 2004 is a leap year. It has 2 odd days.
∴ The day on 8th Feb, 2004 is 2 days before the day on 8th Feb, 2005.
Hence, this day is Sunday.

Question 4.
The radius of a circle is 3 times the radius of another circle, the circumference of the new circle will be how many times the circumference of the smaller circle?
(a) 3 times
(b) \(\frac{1}{3}\) times
(c) 6 times
(d) 9 times
Answer:
(a) 3 times
Explanation:
Let the radius of smaller circle be r.
Then, its circumference = 2πr
New radius = 3r
New circumference = 2π(3r)
= 6πr
= 3 × 2πr
= 3 × (smaller circumference)

Question 5.
On the real number line, if A = [0, 3] and B = [2, 6], then A ∪ B = ________
(a) [0, ∞]
(b) [0, 6]
(c) [3, 2]
(d) [-∞, ∞]
Answer:
(b) [0, 6]
Explanation:
A ∪ B = [0, 6], because A ∪ B = [0, 3] ∪ [2, 6] = [0, 6]

Question 6.
The domain of the relation, R = {(x, y): x, y ∈ Z, xy = 4} is
(a) {-4, -2, -1, 1, 2, 4}
(b) {-2, -1, 1, 2, 4}
(c) {-2, -1, 1, 2}
(d) {1, 2, 4}
Answer:
(a) {-4, -2, -1, 1, 2, 4}
Explanation:
Given, R = {(x, y) : x, y ∈ Z, xy = 4} = {(-4, -1), (-2, -2), (-1, -4), (1, 4), (2, 2), (4, 1)}
Therefore, domain of R = {-4, -2, -1, 1, 2, 4}

Question 7.
In an AP, the pth term is q and (p + q)^th term is 0. Then the qth term is
(a) -p
(b) p
(c) p + q
(d) p – q
Answer:
(b) p
Explanation:
Let a, d be the first term and common difference, respectively,
Therefore, q = a + (p – 1)d …….(i)
and 0 = a + (p + q – 1)d ………(ii)
Subtracting (i) from (ii), we get
qd = -q or d = -1
Substituting in (i), we get,
a = q – (p – 1)(-1)
a = q + p – 1
Now, Tq = a + (q – 1)d
= (q + p – 1) + (q – 1)(-1)
= q + p – 1 – q + 1
= p

Question 8.
Let S be the sum, P be the product and R be the sum of the reciprocals of 3 terms of a G.P. then P²R³ : S³ is equal to
(a) 1 : 1
(b) (common ratio)n : 1
(c) (first term)² : (common ratio)²
(d) none of these
Answer:
(a) 1 : 1
Explanation:
Let the three terms of G.P. be \(\frac{a}{r}\), a, ar.

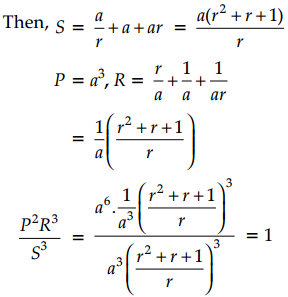
Therefore, the ratio is 1 : 1.

Question 9.
If in certain coding system ‘SHEEP’ is written as ‘GAXXR’ and ‘BLEAT’ as ‘HPXTN’, then code for ‘SLATE’ is
(a) GPTNX
(b) GTPNX
(c) GPTXN
(d) PGTNX
Answer:
(a) GPTNX
Explanation:
Using direct letter coding method, we have

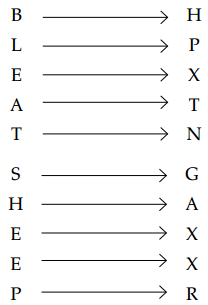
Similarly, using the direct codes

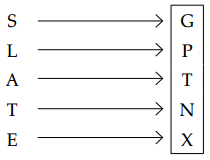
Question 10.
The range of function f(x) = 1 + 3 cos 2x is
(a) [2, 4]
(b) [-2, 4]
(c) [2, -4]
(d) [-2, -4]
Answer:
(b) [-2, 4]
Explanation:
Given, f(x) = 1 + 3 cos 2x
We know that, -1 ≤ cos 2x ≤ 1
⇒ -3 ≤ 3 cos 2x ≤ 3
⇒ 1 – 3 ≤ 1 + 3 cos 2x ≤ 1 + 3
⇒ -2 ≤ 1 + 3 cos 2x ≤ 4
∴ Range of f(x) = [-2, 4]

Question 11.
If x = t² and y = t³ then \(\frac{d^2 y}{d x^2}\) is
(a) \(\frac{3}{2}\)
(b) \(\frac{3}{4t}\)
(c) \(\frac{3}{2t}\)
(d) \(\frac{3}{4}\)
Answer:
(b) \(\frac{3}{4t}\)
Explanation:
Given that, x = t² and y = t³
Then, \(\frac{d x}{d t}\) = 2t and \(\frac{d y}{d t}\) = 3t²
Thus, \(\frac{d y}{d x}=\frac{3 t^2}{2 t}=\frac{3 t}{2}\)
\(\frac{d^2 y}{d x^2}=\frac{3}{2} \frac{d t}{d x}\)
= \(\frac{3}{2} \cdot \frac{1}{2 t}\)
= \(\frac{3}{4t}\)

Question 12.
One number is chosen at random from the number 1 to 21, then the probability that it is prime is
(a) \(\frac{8}{21}\)
(b) \(\frac{1}{21}\)
(c) \(\frac{9}{21}\)
(d) \(\frac{5}{21}\)
Answer:
(a) \(\frac{8}{21}\)
Explanation:
Sample space n(S) = 21
Prime numbers from 1 to 21 are 2, 3, 5, 7, 11, 13, 17, 19.
Let ‘E’ be the event of getting a prime number, then
n(E) = 8
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{8}{21}\)
∴ The probability that the number is prime = \(\frac{8}{21}\)

Question 13.
The following information relates to a sample of size 60, Σx² = 18000, Σx = 960. Then, the variance is
(a) 6.63
(b) 16
(c) 22
(d) 44
Answer:
(d) 44
Explanation:
We know that,
Variance, σ² = \(\frac{\Sigma x_i^2}{N}-\left(\frac{\Sigma x_i}{N}\right)^2\)
= \(\frac{18000}{60}-\left(\frac{960}{60}\right)^2\)
= 300 – 256
= 44

Question 14.
What percentile is 74 in the following group of data (must be in order)?
35, 65, 68, 100, 23, 69, 74, 61, 70, 98, 85, 55
(a) 60th
(b) 90th
(c) 75th
(d) 27th
Answer:
(c) 75th
Explanation:
Arrange the given data in ascending order, we get
23, 35, 55, 61, 65, 68, 69, 70, 74, 85, 95, 100
Here, total no. of observations, Y = 12
and score 74 is at the rank 9, so M = 9
Using formula,
PR = \(\frac{M}{Y}\) × 100
= \(\frac{9}{12}\) × 100
= 75th percentile

Question 15.
The tangent of angle between the lines whose intercepts on the axes are a, -b and b, -a, respectively, is
(a) \(\frac{a^2-b^2}{a b}\)
(b) \(\frac{b^2-a^2}{2}\)
(c) \(\frac{b^2-a^2}{2 a b}\)
(d) None of these
Answer:
(c) \(\frac{b^2-a^2}{2 a b}\)
Explanation:
Equation of line having intercepts a and -b is
\(\frac{x}{a}+\frac{y}{-b}\) = 1
⇒ bx – ay = ab ……(i)
Equation of line having intercepts b and -a is
\(\frac{x}{b}+\frac{y}{-a}\) = 1
⇒ ax – by = ab ……(ii)
Now, slope of equation (i), m1 = \(\frac{b}{a}\)
and slope of equation (ii), m2 = \(\frac{a}{b}\)
∴ tan θ = \(\left|\frac{m_1-m_2}{1+m_1 m_2}\right|=\left|\frac{\frac{b}{a}-\frac{a}{b}}{1+\frac{b}{a} \times \frac{a}{b}}\right|=\frac{b^2-a^2}{2 a b}\)

Question 16.
If the nominal rate of interest is 10% per annum and there is quarterly compounding, the effective rate of interest will be ________
(a) 10.38%
(b) 11.05%
(c) 11.25%
(d) none of these
Answer:
(a) 10.38%
Explanation:
We know that,
effective rate, E = (1 + i)ⁿ – 1
Here, i = 10% quarterly = \(\frac{10}{100} \times \frac{1}{4}\) = 0.025
n = 4
∴ E = (1 + 0.025)⁴ – 1
= (1.025)⁴ – 1
= 1.1038 – 1
= 0.1038
= 10.38%

Question 17.
Integrated Goods and Services Tax is applicable when
(a) Sold in Union territory
(b) Sold from one GST dealer to another GST dealer
(c) Sold within a state
(d) There is interstate supply
Answer:
(d) There is interstate supply
Explanation:
Integrated Goods and Services Tax is applicable when there is interstate supply.

Question 18.
Mr. Ram owns a house property. He lent it to Laxman at ₹ 10,000 p.m. Laxman sublet it to Mr. Maruti on monthly rent of ₹ 20,000 p.m. Rental income of Laxman is taxable under which income head.
(a) Income from salary
(b) Income from other sources
(c) Income from House Property
(d) Capital Gain
Answer:
(b) Income from other sources
Explanation:
Given, Mr. Ram owns a house property and lent it to Laxman at ₹ 10,000 p.m. Laxman sublet it to Mr. Maruti on monthly rent of ₹ 20,000 p.m. Thus, rental income of Laxman is taxable under the head Income from other sources.

Direction (Q.19 & Q.20): In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.

Question 19.
Assertion (A): Decimal equivalent of Binary Number (1011.011)2 is 11.375.
Reason (R): Decimal Value: 1 × 2³ 0 × 2² 1 × 2¹ 1 × 2⁰ . 0 × 2^-1 1 × 2^-2 1 × 2^-3
Answer:
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
Explanation:
Binary to Decimal conversion is obtained by multiplying 2 to the power of base index along with the value at that index position.

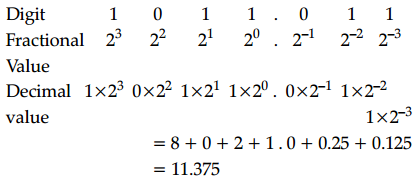
Hence, (1011.011)₂ = (11.375)₁₀

Question 20.
Assertion (A): The Quartile Deviation of the observations: 20, 25, 29, 30, 35, 39, 41, 48, 51, 60 and 70 is 11.
Reason (R): Quartile Deviation = \(\frac{1}{2}\)(Q₃ – Q₁).
Answer:
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
Explanation:
For Q.D., we need to calculate values of Q₃ and Q₁. Also, the given data is already arranged in ascending order.
i.e., 20, 25, 29, 30, 35, 39, 41, 48, 51, 60, 71

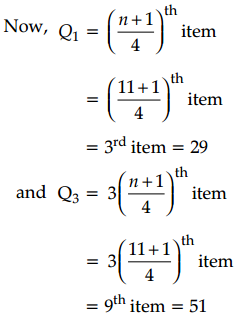
∴ Inter Quartile Range = Q₃ – Q₁ = 51 – 29 = 22
Thus, Quartile Deviation = \(\frac{1}{2}\) × (Q₃ – Q₁)
= \(\frac{1}{2}\) × 22
= 11

Section-B

(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 21.
Two statements followed by two conclusions are given below. You have to decide which of the given conclusions logically follows from the given two statements disregarding commonly known facts.
Statements:
(i) Some vegetables are fruits.
(ii) No fruit is black.
Conclusions:
(I) Some fruits are vegetables.
(II) No vegetable is black.
Answer:
Conclusion I is immediate inference and follows from statement (i). Conclusion II does not follow as vegetable is distributed in conclusion, but not in the statement, Hence, only conclusion I follows.

Question 22.
An unbiased die is thrown twice, let the event A be ‘odd number on first throw’ and B the event ‘odd number on the second throw’. Check independence of the events.
OR
In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random. Find the probability that
(i) The student opted for NCC or NSS.
(ii) The student has opted for neither NCC nor NSS.
Answer:
Sample space of random experiment is given by
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
∴ n(S) = 36
Event A = odd number on first throw
∴ n(A) = 18
Event B = odd number on second throw
∴ n(B) = 18
Therefore, P(A) = \(\frac{n(A)}{n(S)}=\frac{18}{36}=\frac{1}{2}\)
and P(B) = \(\frac{n(B)}{n(S)}=\frac{18}{36}=\frac{1}{2}\)
Also, P(odd number on both throws) = P(A ∩ B)
= \(\frac{n(A \cap B)}{n(S)}\)
= \(\frac{9}{36}\)
= \(\frac{1}{4}\)
Clearly, P(A ∩ B) = P(A) . P(B)
Thus, events A and B are independent.
OR
Let C and S denote the event that the student opted for NCC and NSS respectively.
Then, P(C) = \(\frac{30}{60}=\frac{1}{2}\)
P(S) = \(\frac{32}{60}=\frac{8}{15}\)
P(C ∩ S) = \(\frac{24}{60}=\frac{2}{5}\)
(i) We know that P(C ∪ S) = P(C) + P(S) – P(C ∩ S)

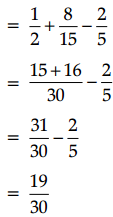
∴ The probability that the student opted for NCC or NSS is \(\frac{19}{30}\).
(ii) P(C’ ∩ S’) = P(C ∪ S)’
= 1 – P(C ∪ S)
= 1 – \(\frac{19}{30}\)
= \(\frac{11}{30}\)
∴ The probability that the student opted neither for NCC nor NSS is \(\frac{11}{30}\)

Question 23.
For a distribution Karl Person’s coefficient of skewness is 0.64, standard deviation is 13 and mean is 59.2. Find mode and median.
OR
Find the mean deviation about the median for the following data:

xi	5	7	9	10	12	15
fi	8	6	2	2	2	6

Answer:
Given, S_k = 0.64, σ = 13 and Mean (\(\bar{x}\)) = 59.2
We know that,
S_k = \(\frac{\text { Mean-Mode }}{\sigma}\)
⇒ 0.64 = \(\frac{59.20-\text { Mode }}{13}\)
⇒ Mode = 59.20 – 8.32 = 50.88
Now, Mode = 3 Median – 2 Mean
⇒ 50.88 = 3(Median) – 2(59.2)
⇒ Median = \(\frac{50.88+118.4}{3}\) = 56.42 (Approx.)
OR

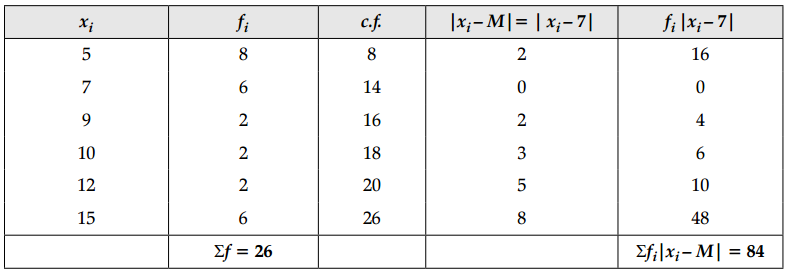
Here, N = 26, which is even.
Median observation are \(\left(\frac{26}{2}\right)^{\mathrm{th}}\) and \(\left(\frac{26}{2}+1\right)^{\mathrm{th}}\) observations
i.e., 13^th and 14^th Observations
i.e., 7 and 7.
Median = \(\frac{7+7}{2}\) = 7
∴ Mean deviation about median (M)
M.D. (M) = \(\frac{\Sigma f_i\left|x_i-M\right|}{\Sigma f_i}\)
= \(\frac{84}{26}\)
= 3.23 (Approx.)

Question 24.
Suppose an investor wants to have 1 lakh to retire 5 years from now. How much would he have to invest today with an annual rate of return equal to 15 percent?
Answer:
We know that,
Present Value, PV = \(\frac{A_n}{(1+i)^n}\)
Here, A_n = 1 lakh = 100000
i = 15% = \(\frac{15}{100}\) = 0.15
n = 5 years
∴ PV = \(\frac{100000}{(1+0.15)^5}=\frac{100000}{(1.15)^5}\)
= \(\frac{100000}{2.0113}\)
= ₹ 49,719.08
Thus, he would invest ₹ 49,719.08 today.

Question 25.
Five 100 W bulbs are used for 10 hours every day for 30 days. Find the cost of electricity if the rate is ₹ 4.00 per unit.
Answer:
Five bulbs consume the power of 100 W each.
The total power consumed by 5 bulbs = 5 × 100
= 500 W
= 0.5 kilowatt (1kW = 1000 W)
Electrical energy consumed daily is, E = P × t
= 0.5 kW × 10 hours
= 5 kWh.
Thus, total electrical energy consumed for 30 days = 5 kWh × 30 days = 150 kWh or 150 units.
The cost of 1 unit of electricity = ₹ 4
Thus, the total cost of electricity = ₹ 4 × 150 = ₹ 600

Section-C

(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 26.
How many different products can be obtained by multiplying two or more of the numbers 2, 5, 6, 7, 9?
Answer:
The given numbers are 2, 5, 6, 7, 9.
The numbers of different products when 2 or more is taking = the number of ways of taking product of 2 numbers + number of ways of taking product of 3 numbers + numbers of ways of taking product of 4 numbers + number of ways of taking 5 together
= ⁵C₂ + ⁵C₃ + ⁵C₄ + ⁵C₅
= \(\frac{5 !}{3 ! 2 !}+\frac{5 !}{2 ! 3 !}+\frac{5 !}{1 ! 4 !}+\frac{5 !}{0 ! 5 !}\)
= \(\frac{5.4}{2.1}+\frac{5.4}{2.1}+\frac{5}{1}+1\)
= 10 + 10 + 5 + 1
= 26

Question 27.
How many words, with or without meaning can be made from the letters of the word ‘MONDAY’, assuming that no letter is repeated, if
(i) 4 letters are used at a time
(ii) all letters are used at a time
(iii) all letters are used but first letter is a vowel.
Answer:
In the word MONDAY, all letters are different.
(i) Out of 6 different letters 4 letters can be selected in ⁶P₄ ways.
∴ Required number of words = ⁶P₄
= \(\frac{6 !}{(6-4) !}\)
= \(\frac{6 \times 5 \times 4 \times 3 \times 2 !}{2 !}\)
= 360

(ii) The word ‘MONDAY’ has 6 different letters.
Number of ways taking 6 letters at a time = ⁶P₆
∴ Required number of words = ⁶P₆
= \(\frac{6 !}{(6-6) !}\)
= \(\frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{0 !}\)
= 720

(iii) First, we will fix the vowel.
In the word MONDAY, there are two vowels O and A.
∴ First letter can be chosen 2 ways.
Number of ways taking 5 different letters from remaining 5 letters = ⁵P₅
∴ Required number of words = ⁵P₅
= \(\frac{5 !}{(5-5) !}=\frac{5 !}{0 !}\)
= 5 × 4 × 3 × 2 × 1
= 120
Hence, total number of ways = 2 × 120 = 240

Question 28.
In a family of seven members, three generations are living together. The family has two married couples with two children each. Dharmesh has two grandchildren. There are two housewives. Dharmesh who is Bhavesh’s father, is a Doctor and earns the most. Yuvraj is the son of Anuja. Anuja is married to an Engineer who is Kamla’s son. Sonal is the grand-daughter of one of the housewives eq. and she is a classical dancer. Sarika is the sister of an Engineer and herself is a Teacher.
(i) What is Bhavesh’s profession?
(ii) How many female members are there in the family?
(iii) Who are the childern’s of Kamla?
Answer:
We first draw family chart to understand the relationship with each other.

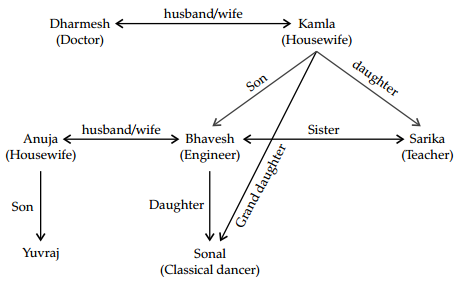
In the above chart, we can see that Dharmesh (Doctor) is the husband of Kamla (housewife). They have two children, one son and one daughter namely Bhavesh (Engineer) and Sarika (Teacher). Bhavesh is married to Anuja (Housewife) and they have two children namely Yuvraj and Sonal.
(i) Bhavesh’s profession in Engineer.
(ii) There are four females in the family.
(iii) Bhavesh and Sarika are the children of Kamla.

Question 29.
Find the value of k, f or which f(x) = \(\left\{\begin{array}{ccc}
\frac{\sqrt{1+k x}-\sqrt{1-k x}}{x}, & \text { if } & -1 \leq x<0 \\
\frac{2 x+1}{x-1}, & \text { if } & 0 \leq x<1
\end{array}\right.\) is continuous at x = 0.
OR
Differentiate f(x) = x5ex + x3 log x – 2x with respect to x.
Answer:

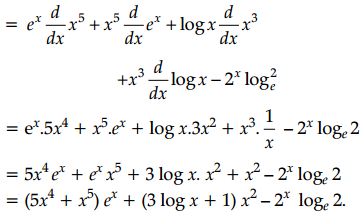
Question 30.
Compute the coefficient of rank correlation between sales and advertisement expressed in thousands of ₹ from the following table:

Sales:	90	85	68	75	82	80	95	70
Advertisement:	7	6	2	3	4	5	8	1

OR
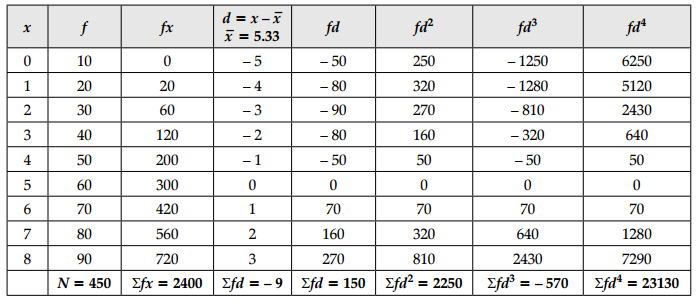
Calculate the first four central moments from the following data:

x	0	1	2	3	4	5	6	7	8
f	10	20	30	40	50	60	70	80	90

Answer:
Let the rank given to sales be denoted by x and rank of advertisement be denoted by y. We note that since the highest sales as in the given data, is 95, it is to be given rank 1, the second highest sales 90 is to be given rank 2 and finally rank 8 goes to the lower sales, namely 68. We have given rank to the other variable advertisement in a similar manner.

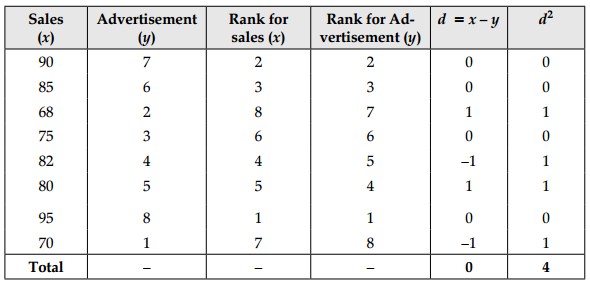
Since, n = 8 and Σd² = 4

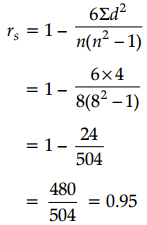
The high positive value of the rank correlation coefficient indicates that there is a very good amount of agreement between sales and advertisement.
OR

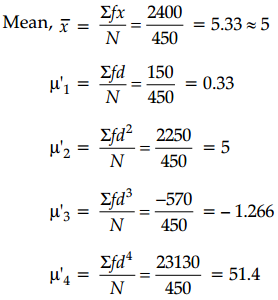
Question 31.
A mortgage of ₹ 1,90,000 is required to purchase a house. The mortgage will be repaid with equal monthly payments over 25 years at 8% compounded monthly.
(a) What is the monthly payment?
(b) What is the total interest paid over the 25 years?
[Given that, (1.006)300 = 7.3402]
Answer:
(a) Here, n = 25 × 12 = 300
i = 8% monthly = \(\frac{8}{100} \times \frac{1}{12}\) = 0.006
Present value, P.V. = ₹ 190,000
We know that, P.V. = \(\text { C.F. } \times \frac{\left[(1+i)^n-1\right]}{i(1+i)^n}\)

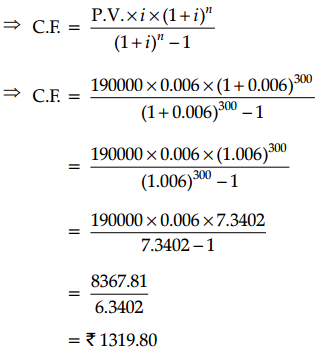
(b) Interest = 1319.80 × 300 – 190,000
= 395, 490 – 190,000
= ₹ 205,940

Section-D

(This section comprises long answer type questions (LA) of 5 marks each)

Question 32.
If p, q, r are in G.P. and the equations px² + 2qx + r = 0 and dx² + 2ex + f = 0 have a common root, then show that \(\frac{d}{p}, \frac{e}{q}, \frac{f}{r}\) are in A.P.
OR
Let the sum of n, 2n, 3n terms of an A.P. be S1, S2, and S3 respectively. Show that S₃ = 3(S₂ – S₁).
Answer:
It is given that p, q, r are in G.P.
∴ q² = pr
Now, px² + 2qx + r = 0
⇒ px² + 2x.√pr + r = 0
⇒ (x.√p + √r)2 = 0
⇒ √px + √r = 0
⇒ x = \(-\sqrt{\frac{r}{p}}\)
It is given that the equations px² + 2qx + r = 0 and dx² + 2ex + f = 0 have a common root and the equation px² + 2qx + r = 0 has equal roots equal to \(-\sqrt{\frac{r}{p}}\).
∴ \(-\sqrt{\frac{r}{p}}\) is a root of the equation dx² + 2ex + f = 0

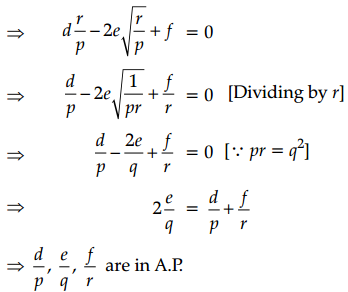
OR
Let a and d be the first term and common difference respectively of an A.P.
Given, S₁ = Sum of n terms = \(\frac{n}{2}\)[2a + (n – 1)d] ……(i)
S₂ = Sum of 2n terms = \(\frac{2n}{2}\)[2a + (2n – 1)d] ……(ii)
S₃ = Sum of 3n terms = \(\frac{3n}{2}\)[2a + (3n – 1)d] …….(iii)
Now, we have to prove S₃ = 3(S₂ – S₁)
Now, R.H.S. = 3(S₂ – S₁)
= 3[\(\frac{2n}{2}\)[2a + (2n – 1)d] – \(\frac{n}{2}\)[2a + (n – 1)d] [from Equations (i) and (ii)]
= \(\frac{3n}{2}\)[2{2a + (2n – 1)d} – {2a + (n – 1)d}
= \(\frac{3n}{2}\)[4a + 2(2n – 1)d – 2a – (n – 1)d]
= \(\frac{3n}{2}\)[(4a – 2a) + d(4n – 2 – n + 1)]
= \(\frac{3n}{2}\)[2a + (3n – 1)d]
= S₃ [from Equation (iii)]
= L.H.S.
∴ L.H.S. = R.H.S.

Question 33.
Find the domain and range of the following functions:
(i) f(x) = \(\frac{1}{\sqrt{x-5}}\)
(ii) f(x) = \(\left\{\left(\frac{x^2-1}{x-1}\right): x \in R, x \neq 1\right\}\)
Answer:
(i) Given, f(x) = \(\frac{1}{\sqrt{x-5}}\)
f(x) is defined, if x – 5 > 0
⇒ x > 5
∴ Domain of f = (5, ∞)
Let f(x) = y
∴ y = \(\frac{1}{\sqrt{x-5}}\)
⇒ \(\sqrt{x-5}=\frac{1}{y}\)
⇒ x – 5 = \(\frac{1}{y^2}\)
⇒ x = \(\frac{1}{y^2}\) + 5
∴ x ∈ (5, ∞) ∈ y ⇒ R⁺
Hence, range of f = R⁺ > 5.
(ii) Given, f(x) = \(\frac{x^2-1}{x-1}\), x ≠ 1,
clearly f(x) is defined for all real values of x except x = 1
i.e., Domain off(x) = R – {1}
Now, f(x) = \(\frac{x^2-1}{x-1}\)
⇒ f(x) = \(\frac{(x-1)(x+1)}{x-1}\)
⇒ f(x) = x + 1, x ≠ 1
Range of f(x) = R – {2}
[∴ At x = 1, f(x) = 1 + 1 = 2]

Question 34.
A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn at random and are found to be hearts. Find the probability of the missing card to be a heart.
OR
A factory has three machines A, B and C producing 1500, 2500 and 3000 bulbs per day, respectively. Machine A produces 1.5% defective bulbs, machine B produces 2% defective bulbs and machine C produces 2.5% defective bulbs. At the end of the day, a bulb is drawn at random and is found to be defective. What is the probability that the defective bulb has been produced by machine B?
Answer:
Let C₁, C₂, C₃ and C₄ be the events that the lost card is of heart, spade, diamond or club, respectively.
Clearly, P(C₁) = P(C₂) = P(C₃) = P(C₄) = \(\frac{13}{52}=\frac{1}{4}\)
Let S be the event of drawing two cards of heart from the remaining 51 cards. Here, we wish to find \(P\left(\frac{C_1}{S}\right)\)
Now, \(P\left(\frac{S}{C_1}\right)\) is the probability of drawing two heart cards from 51 cards given that one heart card is lost


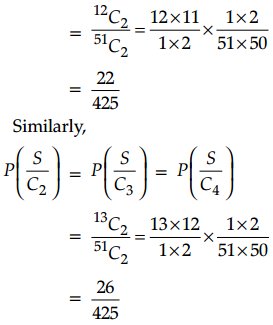
OR
Given that, total daily production of bulbs = 1500 + 2500 + 3000 = 7000 bulbs.
Let A, B and C be the event if drawing a bulb produced by machines A, B and C respectively.
P(A) = \(\frac{1500}{7000}=\frac{3}{14}\)
P(B) = \(\frac{2500}{7000}=\frac{5}{14}\)
P(C) = \(\frac{3000}{7000}=\frac{3}{7}\)
Let F be the event of producing a defective bulb

Question 35.
Compute the taxable value of the perquisite in respect of medical facilities availed of by X from his employer in the following situations:
(a) the employer reimburses the following medical expenses:
(i) Treatment of X by his family physician ₹ 8,400
(ii) Treatment of Mrs. X in a private nursing home ₹ 7,200
(iii) Treatment of X’s mother (dependent upon him) ₹ 2,400 by a private doctor
(iv) Treatment of X’s brother (not dependent upon him) ₹ 800
(v) Treatment of X’s grandfather (dependent upon him) ₹ 3,000
(b) The employer reimburses an insurance premium of ₹ 6,000 paid by X under a health insurance scheme on the life of X and his wife.
(c) The employer maintains a hospital for the employees where they and their family members are provided free treatment. The expenses on treatment of X and his family members during the previous year 2021-22 were as under:

Particulars	Amount (₹)
(i) treatment of X’s major son (dependent upon him)	4,400
(ii) treatment of X	10,400
(iii) treatment of X’s uncle	9,200
(iv) treatment of Mrs. X	16,000
(v) treatment of X’s widowed sister (dependent upon him)	8,200
(vi) treatment of X’s handicapped nephew	5,000

(d) Expenses on cancer treatment of married daughter of X at Tata Memorial Hospital, Mumbai paid by the employer ₹ 1,00,000 and reimbursement of expenses for medical treatment of himself amounting to ₹ 40,000.
Answer:
(a)

Particulars	Expenses
(i) Treatment of X	8,400
(ii) Treatment of Mrs. X	7,200
(iii) Treatment of X’s mother	2,400
(iv) Treatment of X’s brother	800
(v) Treatment of X’s grandfather Less. Exempt	3,000
Total	21,800

Hence ₹ 21,800 shall be taxable perquisite w.e.f. assessment year 2021-22, medical reimbursement shall be fully taxable.
(b) Reimbursement of insurance premium on the health of the employee and his family members is a tax-free perquisite. Hence nothing is taxable.
(c) The expenses of medical treatment of the employee and his family members in a hospital maintained by the employer are tax-free. Therefore, expenses on treatment of X, X’s major son, X’s widowed sister and Mrs. X are not taxable. Only the following expenses are taxable:

Particulars	Amount (₹)
(i) Treatment of X’s uncle	9,200
(ii) Treatment of X’s handicapped nephew	5,000
Taxable perquisite	14,200

(d) Expenses on medical treatment of the employee/family members in respect of prescribed diseases, in any hospital approved by the Chief Commissioner of Income-tax, are tax-free. In this case as cancer is a prescribed disease and Tata Memorial Hospital, Mumbai is approved by Chief Commissioner of Income-tax, there is no taxable perquisite. However, ₹ 40,000 reimbursement of medical expenses, shall be taxable perquisite in this case.

Section-E

(This section comprises 3 source-based questions (Case Studies) of 4 marks each)

Question 36.
Few students with their teacher went to an education trip. They saw few people working in the field. The teacher discussed a few concepts related to time and work, which are as follows:
Rule 1: If M1 persons can do W1 work in D1 days and M2 persons can do W2 work in D2 days, then we can say M1 × D1 × W2 = M2 × D2 × W2
If the persons work T1 and T2 hours per day, respectively, then the equation gets modified to
M₁ × D₁ × W₂ × T₁ = M₂ × D₂ × W₁ × T₂
If the person’s efficiency are E1 and E2 respectively, then
M₁ × D₁ × W₂ × T₁ × E₁ = M₂ × D₂ × W₁ × T₂ × E₂
Rule 2: If A can do a piece of work in n days, then the work done by A in one day = \(\frac{1}{n}^{\text {th }}\) part of whole work.
Rule 3: If A’s one day’s work = \(\frac{1}{n}^{\text {th }}\) part of the whole work, then A can finish the work in n days.
Rule 4: If A can do a work in D₁ days and B can do the same work in D₂ days, then A and B together can do the same work in \(\left(\frac{D_1 \times D_2}{D_1+D_2}\right)\) days.

On the basis of this information teacher ask students various questions as mentioned below:
(i) If 15 men working 9 hours a day, can reap a field in 16 days, in how many days will 18 men reap the field, working 8 hours a day?
OR
‘A’ can do a piece of work in 5 days and ‘B’ can do it in 6 days. How long will they take if both work together?
(ii) A man can do a piece of work in 5 days, but with the help of his son, he can do it in 3 days. In what time can the son do it alone?
(iii) A can do a piece of work in 80 days. He works at it for 10 days and then B alone finishes the remaining work in 42 days. In how much time will A and B, working together, finish the work?
Answer:
(i) Here, M₁ = 15, D₁ = 16, T₁ = 9 hours, M₂ = 18 and T₂ = 8 hours
Using formula,
M₁ × D₁ × T₁ = M₂ × D₂ × T₂
⇒ D₂ = \(\frac{M_1 \times D_1 \times T_1}{M_2 \times T_2}\)
⇒ D₂ = \(\frac{15 \times 16 \times 9}{18 \times 8}\) = 15 days
Hence, required number of days are 15.
OR
Suppose, A can do a piece of work in D₁ days and B can do the same work in D₂ days.
Here, given D₁ = 5 days and D₂ = 6 days
Thus, A and B can do this work in \(\frac{D_1 \times D_2}{D_1+D_2}\) days
= \(\frac{5 \times 6}{5+6}\)
= \(\frac{30}{11}\)
= 2\(\frac{8}{11}\) days
(ii) Son’s 1 day’s work = \(\left(\frac{1}{3}-\frac{1}{5}\right)=\frac{2}{15}\)
∴ The son alone can do the work in \(\frac{15}{2}=7 \frac{1}{2}\) days
(iii) Work done by A in 10 days = \(\frac{1}{8}\) × 10 = \(\frac{1}{8}\)
Remaining work = 1 – \(\frac{1}{8}\) = \(\frac{7}{8}\)
Now, \(\frac{7}{8}\) work is done by B in 42 days
Whole work will be done by B in (42 × \(\frac{8}{7}\)) = 48 days
∴ A’s 1 day’s work = \(\frac{1}{80}\) and B’s 1 days’ work = \(\frac{1}{48}\)
∴ (A + B)’s 1 days’ work = \(\frac{1}{80}+\frac{1}{48}=\frac{8}{240}=\frac{1}{30}\)
Hence, both will finish the work in 30 days.

Question 37.
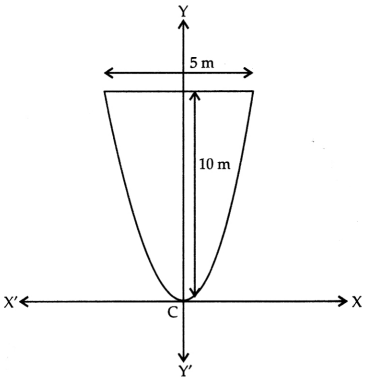
Rahul is playing with long string, he hang the ends of the string at two points on the wall. Now, it is in the form of parabola with its vertical axis and is 10 m high and 5 m wide at its base as shown in the following figure:

On the basis of the above information answer the following questions:
(i) What is the standard equation of parabola in this case?
(ii) Find the value of a in the standard equation.
(iii) How wide is it 2 m from the vertex of the parabola?
OR
Find the equation of the parabola whose focus is (6, 0) and the directrix is x = 0.
Answer:
(i) The equation of the parabola is of the form x² = 4ay (as it opening upwards).
(ii) It can be clearly seen that the parabola passes through point (\(\frac{5}{2}\), 10).
\(\left(\frac{5}{2}\right)^2\) = 4a(10)
⇒ a = \(\frac{25}{4 \times 4 \times 10}\)
⇒ a = \(\frac{5}{32}\)
(iii) The equation of parabola is x² = 4ay
⇒ x² = 4(\(\frac{5}{32}\))y
⇒ x² = (\(\frac{5}{8}\))y

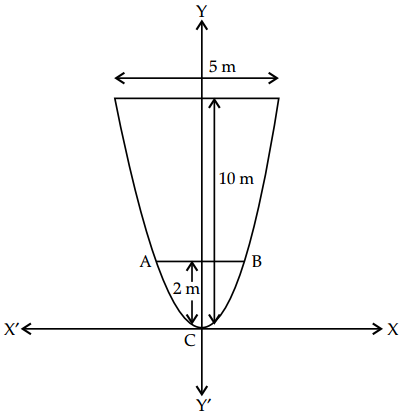
AB = 2 × \(\sqrt{\frac{5}{4}}\) m
= \(\sqrt{5}\) (approx.)
= 2.23 m (approx.)
OR
Let P(x, y) be any point on the parabola.
Join the point P to the focus S(6, 0) and draw PM perpendicular from P upon the directrix x = 0 (y-axis). Then by the definition of parabola, we have
SP = PM
⇒ \(\sqrt{(x-6)^2+(y-0)^2}\) = x
⇒ (x – 6)² + y² = x²
⇒ x² + 36 – 12x + y² = x²
⇒ y² = 12x – 36

Question 38.
In a class of Statistics, the teacher was discussing the concept of Measures of Correlation, in which he was discussing Karl Pearson’s Coefficient of Correlation. During his class, he discussed the following few points on this:
This is the best method for finding a correlation between two variables provided the relationship between the two variables is linear. This method is also known as product-moment correlation coefficient. Pearson’s correlation coefficient may be defined as the ratio of covariance between the two variables to the product of the standard deviations of the two variables.
If the two variables are denoted by x and y and of the corresponding bivariates data are (x_i, y_i) for i = 1, 2, 3,…., n, then the coefficient of correlation between x and y due to Karl Pearson is given by:


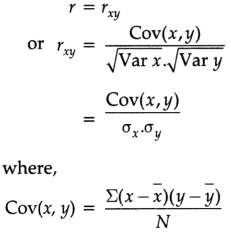
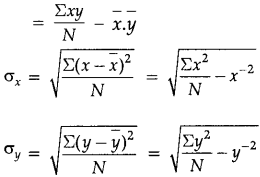
If x – \(\bar{x}\), y – \(\bar{y}\) are small fractions, we use
r = \(\frac{\Sigma(x-\bar{x})(y-\bar{y})}{\sqrt{\Sigma(x-\bar{x})^2} \sqrt{\Sigma(y-\bar{y})^2}}\)
If x, y are small numbers, we use
r = \(\frac{\Sigma x y-\frac{1}{N} \Sigma x \Sigma y}{\sqrt{\Sigma x^2-\frac{1}{N}(\Sigma x)^2} \sqrt{\Sigma y^2-\frac{1}{N}(\Sigma y)^2}}\)
If x, y are large numbers, we use assumed mean A and B and u = x – A, v = y – B
r = \(\frac{\Sigma u v-\frac{1}{N} \sum u \Sigma v}{\sqrt{\Sigma u^2-\frac{1}{N}(\Sigma u)^2} \sqrt{\Sigma v^2-\frac{1}{N}(\Sigma v)^2}}\)
On the basis of the above information, answer the following questions:
(i) Compute Cov(x, y) for the following pair of observations:
(15, 44), (20, 43), (25, 45), (30, 37), (40, 34), (50, 37)
(ii) Find Karl Pearson’s coefficient of correlation between X and Y for the following:

x	5	4	3	2	1
y	4	2	10	8	6

Answer:
(i) Here, \(\bar{x}=\frac{15+20+25+30+40+50}{6}=\frac{180}{6}\) = 30
and \(\bar{y}=\frac{44+43+45+37+34+37}{6}=\frac{240}{6}\) = 40
Now, construct the following table:

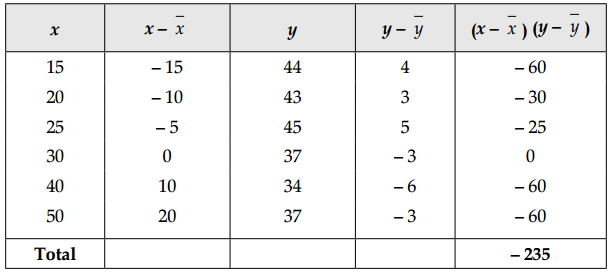
So, Cov(x, y) = \(\frac{1}{N} \Sigma(x-\bar{x})(y-\bar{y})\)
= \(\frac{1}{6}\)(-235)
= -39.17
OR
(ii)

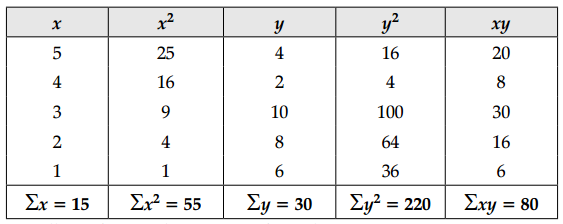
Here, N = 5 and x, y are small numbers, so here we use formula:

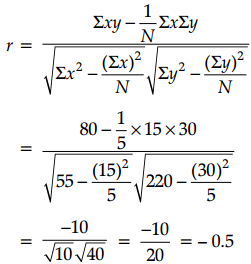
Read More:

How To Track Gift Nifty