CBSE Sample Papers for Class 11 Applied Mathematics Set 2 with Solutions

Students can access the CBSE Sample Papers for Class 11 Applied Mathematics with Solutions and marking scheme Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Applied Mathematics Set 2 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

• This Question paper contains five sections A, B, C, D and E. Each section is compulsory. However, there is some internal choice in some questions.
• Section A has 18 MCQs and 2 Assertion Reason-based questions of 1 mark each.
• Section B has 5 Very Short Answer (VSA) questions of 2 marks each.
• Section C has 6 Short Answer (SA) questions of 3 marks each.
• Section D has 4 Long Answer (LA) questions of 5 marks each.
• Section E has 3 source-based/case-based/passage-based/integrated units of assessment (4 marks each) with subparts.
• Internal Choice is provided in 2 questions in Section B, 2 questions in Section C, 2 Questions in Section D. You have to attempt only one alternative in all such questions.

Section-A

(All Questions are compulsory. No internal choice is provided in this section)

Question 1.
\(2^{1 / 2} \cdot 4^{3 / 4}\) is equal to
(a) a fraction
(b) a positive integer
(c) a negative integer
(d) none of these
Answer:
(b) a positive integer
Explanation:

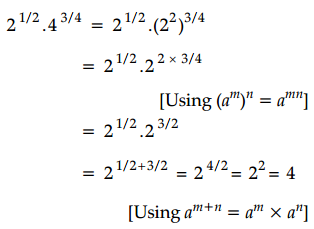
Question 2.
A batsman makes a score of 87 runs in the 17th inning and thus increases his average by 3. His average after the 17th inning is:
(a) 20
(b) 22
(c) 25
(d) 39
Answer:
(d) 39
Explanation:
Let the average after 17th inning = x
The, average after 16th inning = x – 3
∴ 16(x – 3) + 87 = 17x
⇒ x = 87 – 48 = 39

Question 3.
A clock is started at noon. By 10 minutes past 5, the hour hand has turned through
(a) 145°
(b) 150°
(c) 155°
(d) 160°
Answer:
(c) 155°
Explanation:
Angle traced by hour hand in 12 hours = 360°
Angle traced by hour hand in 5 hrs 10 min (\(\frac{31}{6}\) hours) = \(\left(\frac{360}{12} \times \frac{31}{6}\right)^{\circ}\) = 155°

Question 4.
‘A’ does a work in 10 days and ‘B’ does the same work in 15 days. In how many days they together will do the same work?
(a) 5 days
(b) 6 days
(c) 8 days
(d) 9 days
Answer:
(b) 6 days
Explanation:
A’s 1 day’s work = \(\frac{1}{10}\)
B’s 1 day’s work = \(\frac{1}{15}\)
∴ (A + B)’s 1 day’s work = \(\frac{1}{10}+\frac{1}{15}=\frac{1}{6}\)
So, both together will finish the work in 6 days.

Question 5.
If set A = {-2, 2} and B = {x : x ∈ I, x² – 4 = 0}, then relation between set A and set B is
(a) A = B
(b) A ≠ B
(c) Data is insufficient
(d) None of these
Answer:
(a) A = B
Explanation:
Given, A = {-2, 2} and B = {x : x ∈ I, x² – 4 = 0}
∴ x² – 4 = 0
⇒ (x – 2)(x + 2) = 0
⇒ x = -2, 2
or, B = {-2, 2}
Hence, A = B

Question 6.
A sequence may be defined as a
(a) relation, whose range ≤ N (natural number)
(b) function, whose range ≤ N
(c) function, whose domain ≤ N
(d) progression have real values
Answer:
(c) function, whose domain ≤ N
Explanation:
A sequence is a function f : N → X having domain ≤ N.

Question 7.
The 20th term of the sequence \(\frac{5}{2}, \frac{5}{4}, \frac{5}{8}, \ldots \ldots\)
(a) \(\frac{5}{2^{19}}\)
(b) \(\frac{5}{2^{20}}\)
(c) \(\frac{1}{2^{19}}\)
(d) \(\frac{1}{2^{20}}\)
Answer:
(b) \(\frac{5}{2^{20}}\)
Explanation:
The given sequence \(\frac{5}{2}, \frac{5}{4}, \frac{5}{8}, \ldots \ldots\) is a G.P. with first term, a = \(\frac{5}{2}\) and common ratio r = \(\frac{1}{2}\).
∵ T_n = a_n = ar^n-1
∴ a₂₀ = \(a r^{20-1}=\frac{5}{2} \times\left(\frac{1}{2}\right)^{19}=\frac{5}{2^{20}}\)

Question 8.
Danger leads to
(a) Enemy
(b) Attack
(c) Fear
(d) Help
Answer:
(c) Fear
Explanation:
Among the four options it looks as if all the four can be filled in the blank space. But we have to select one that is most appropriate and indispensable. We have experienced in our life that danger always leads fear. All the other options are remote but only fear is the most proximate option.

Question 9.
Let f and g be real functions where f(x) = \(\sqrt{x+4}\), x ≥ -4 and g(x) = \(\sqrt{x-4}\), x ≥ 4. Then function fg is
(a) \(\sqrt{x^2-16}\)
(b) \(\sqrt{x^2-4}\)
(c) \(\sqrt{x^2+1}\)
(d) \(\sqrt{x^2-1}\)
Answer:
(a) \(\sqrt{x^2-16}\)
Explanation:
fg = f(x) g(x)
= \(\sqrt{x+4} \sqrt{x-4}\)
= \(\sqrt{x^2-16}\)

Question 10.
\(\lim _{x \rightarrow 1} \frac{x^m-1}{x^n-1}\) is equal to
(a) \(\frac{m}{n}\)
(b) \(\frac{n}{m}\)
(c) \(\frac{1}{m}\)
(d) \(\frac{1}{n}\)
Answer:
(a) \(\frac{m}{n}\)
Explanation:

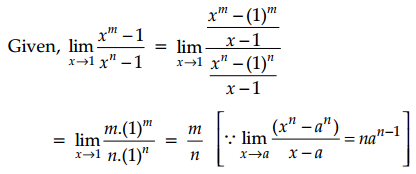
Question 11.
If f(x) = \(1+x+\frac{x^2}{2}+\ldots+\frac{x^{100}}{100}\), then f'(1) is equal to
(a) \(\frac{1}{100}\)
(b) 100
(c) 0
(d) Does not exist
Answer:
(b) 100
Explanation:
Given,

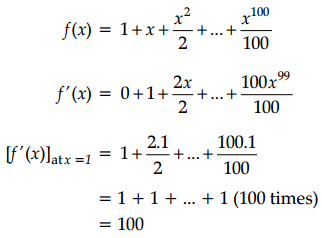
Question 12.
The probability that the home team will win an upcoming football game is 0.77, the probability that it will tie the game is 0.08 and the probability that it will lose the game is
(a) 0.77
(b) 0.88
(c) 0.85
(d) 0.15
Answer:
(d) 0.15
Explanation:
Given, P(loosing the game) = 1 – [P (winning football game) + P(the game will tie)]
= 1 – (0.77 + 0.08)
= 1 – 0.85
= 0.15

Question 13.
The mean derivation of the data 3,10,10,4,7,10,5 from the mean is
(a) 2
(b) 2.57
(c) 3
(d) 3.75
Answer:
(b) 2.57
Explanation:
Given observations are 3, 10, 10, 4, 7, 10, 5

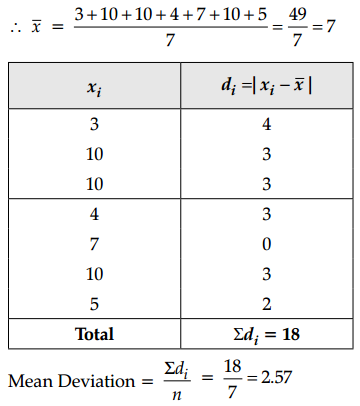
Question 14.
If x₁, x₂,……, x_n be n observations and \(\bar{x}\) be their arithmetic mean. Then, the formula for the standard deviation is given by
(a) \(\Sigma\left(x_i-\bar{x}\right)^2\)
(b) \(\frac{\Sigma\left(x_i-\bar{x}\right)^2}{n}\)
(c) \(\sqrt{\frac{\Sigma\left(x_i-\bar{x}\right)^2}{n}}\)
(d) \(\sqrt{\frac{\Sigma x_i^2}{n}+\bar{x}^2}\)
Answer:
(c) \(\sqrt{\frac{\Sigma\left(x_i-\bar{x}\right)^2}{n}}\)
Explanation:
The formula for S.D., σ = \(\sqrt{\frac{\Sigma\left(x_i-\bar{x}\right)^2}{n}}\)

Question 15.
The X- intercept of the line 3y + 2 = 0 is
(a) \(\frac{-2}{3}\)
(b) \(\frac{3}{2}\)
(c) \(\frac{2}{3}\)
(d) None of these
Answer:
(d) None of these
Explanation:
Given line 3y + 2 = 0
⇒ 3y = – 2
⇒ y = \(\frac{-2}{3}\)
⇒ \(\frac{\frac{y}{-2}}{3}\) = 1
Here, Y-intercept is \(\frac{-2}{3}\) and no intercept along X-axis.

Question 16.
The equation of the circle with centre (2, 2) and which passes through the point (4, 5) is
(a) x² + y² – 4x – 4y = 5
(b) x² + y² + 4x + 4y = 5
(c) x² + y² – 4x + 4y = 5
(d) x² + y² + 4x – 4y = 5
Answer:
(a) x² + y² – 4x – 4y = 5
Explanation:

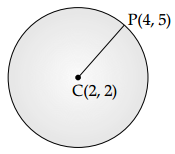
The centre of the circle is C(2, 2) and it passes through point P(4, 5).
∴ Radius of circle = CP
= \(\sqrt{(4-2)^2+(5-2)^2}\)
= \(\sqrt{13}\)
∴ The equation of the circle is (x – 2)² + (y – 2)² = (\(\sqrt{13}\))2
⇒ (x² – 4x + 4) + (y² – 4y + 4) = 13
⇒ x² + y² – 4x – 4y = 13 – 8
⇒ x² + y² – 4x – 4y = 5

Question 17.
Energy is equal to
(a) Power × Time
(b) Power
(c) Power/Time
(d) None of these
Answer:
(a) Power × Time
Explanation:
Energy = Power × Time

Question 18.
In India, the GST is based on the dual model GST adopted in:
(a) UK
(b) Canada
(c) USA
(d) Japan
Answer:
(b) Canada

Direction (Q.19 & Q.20): In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.

Question 19.
Assertion (A): If the capacity of a cylindrical tank is 1848 m³ and the diameter of its base is 14 m, then the depth of the tank is 12 m.
Reason (R): Capacity of tank = πr²h
Answer:
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
Explanation:
Let the depth of the tank be h metres.
Then, π × (7)² × h = 1848
⇒ h = 1848 × \(\frac{7}{22} \times \frac{1}{7 \times 7}\)
⇒ h = 12 m

Question 20.
Assertion (A): Simple interest on ₹ 2500 at the rate of 5% per annum for five years is ₹ 650.
Reason (R): Simple interest is given by SI = \(\frac{P \times R \times T}{100}\)
Answer:
(d) (A) is false but (R) is true.
Explanation:
Simple interest on ₹ 2500 at the rate of 5% per annum for 5 years is given by
S.I. = \(\frac{P \times R \times T}{100}\)
= \(\frac{2500 \times 5 \times 5}{100}\)
= ₹ 625
Therefore, Assertion is false but reason is true.

Section-B

(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 21.
In this question, below are two statements followed by two conclusions numbered I and II. You have to take the two given statements to be variance from commonly known facts and decide which of the given conclusions logically follows the two given statements disregarding commonly known facts.
Give answer:
(a) if only conclusion I follows
(b) if only conclusion II follows
(c) if either I or II follows
(d) if neither I nor II follows
(e) if both I and II follow
Statements:
(i) Some fools are intelligent.
(ii) Some intelligent are great.
Conclusions:
I. Some fools are great.
II. All great are intelligent.
Answer:
(i) Conclusion I is mediate inference and conclusion II is immediate inference. Since middle term is not distributed conclusion I does not follow. Conclusion II is not true as per the rule of immediate inference. Hence, neither I nor II follows.

Question 22.
A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that all the three balls are red.
OR
A young man visits a hospital for medical check up. The probability that he has lungs problem is 0.55, heart problem is 0.29 and either lungs or heart problem is 0.57. What is the probability that he has both type of problems: lungs as well as heart?
Answer:
∵ Number of red balls = 8
and number of white balls = 5
P(all the three balls are red)

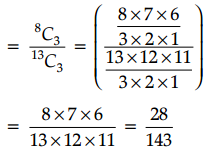
OR
Let ‘L’ and ‘H’ be the events that the young man has lungs problem and heart problem respectively.
∴ P(L) = 0.55, P(H) = 0.29, P(L ∪ H) = 0.57, P(L ∩ H) = ?
We know that,
P(L ∪ H) = P(L) + P(H) – P(L ∩ H)
⇒ P(L ∩ H) = P(L) + P(H) – P(L ∪ H)
= 0.55 + 0.29 – 0.57
= 0.27
∴ The probability that he has both problems is 0.27.

Question 23.
For a certain frequency distribution \(\mu_1^{\prime}\) = 2, \(\mu_2^{\prime}\) = 18 and \(\mu_3^{\prime}\) = 100, find S_k.
OR
The marks of 9 students in a test were 13, 17, 20, 5, 3, 3, 18, 15, and 20. Find the 6th decile and P₆₂.
Answer:
Given, \(\mu_1^{\prime}\) = 2, \(\mu_2^{\prime}\) = 18 and \(\mu_3^{\prime}\) = 100
Here, we need to calculate the central moments μ₂ and μ₃.
μ₂ = σ² = \(\mu_2^{\prime}-\left(\mu_1^{\prime}\right)^2\)
= 18 – (2)²
= 18 – 4
= 14
μ₃ = \(\mu_3^{\prime}-3 \mu_2^{\prime} \mu_1^{\prime}+2\left(\mu_1^{\prime}\right)^3\)
= 100 – 3(18)(2) + 2(2)³
= 100 – 108 + 16
= 8
Now, σ = \(\sqrt{\mu_2}\)
= \(\sqrt{14}\)
= 3.74 (Approx.)
S_k = \(\frac{\mu_3}{\sigma^3}\)
= \(\frac{8}{(3.74)^3}\)
= 0.1529 (Approx.)
OR
First we have to arrange the data in ascending order:
3, 3, 5, 13, 15, 17, 18, 20, 20
Here, n = 9
6th decile, D₆ = \(\frac{6(9+1)}{10}^{\text {th }}\) value
= 6th value
= 17
and P₆₂ = \(\frac{62(9+1)}{100}^{\text {th }}\) value
= 6.2th value
= 6th value + 0.2 (7th value – 6th value)
= 17 + 0.2(18 – 17)
= 17.2

Question 24.
What do you understand by water tariff and fixed water charge?
Answer:
A water tariff (often called water rate) is a price assigned to water supplied by a public utility through a piped network to its customers. The term is also often applied to wastewater tariffs. Water and wastewater tariffs are not charged for water itself, but to recover the costs of water treatment, water storage, transporting it to customers, collecting and treating wastewater, as well as billing and collection.

With a fixed water charge, the consumer pays a monthly water bill, which is the same independent of the volume consumed. In absence of a water metering system, a fixed water charge is the only possible tariff structure. Fixed water charges are commonly found in countries where water has historically been abundant and hence metering was not needed to give people an incentive to reduce water consumption. Fixed charges are still quite widely used in industrialised countries, such as Canada, Norway and United Kingdom. Despite a lot of water shortages, we find fixed charges also in many small and medium size cities in India, were they are still the most prevalent way to calculate the monthly water bill.

Question 25.
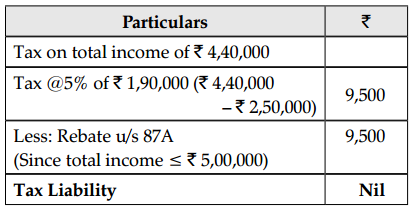
Mr. Raghav aged 26 years and a resident in India, has a total income of ₹ 4,40,000, comprising his salary income and interest on bank fixed deposit. Compute his tax liability for A.Y. 2021-22.
Answer:
Computation of tax liability of Mr. Raghav for A.Y. 2021-22

Section-C

(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 26.
The A.M. and G.M. between two positive numbers are 10 and 8 respectively find the numbers.
OR
If in an A.P. \(\frac{a_7}{a_{10}}=\frac{5}{7}\), find \(\frac{a_4}{a_7}\).
Answer:
Let the two positive numbers be a and b. Then
A.M. = \(\frac{a+b}{2}\) = 10 (given)
⇒ a + b = 20 …..(i)
and G.M. = \(\sqrt{ab}\) = 8 (given)
⇒ ab = 64
⇒ a(20 – a) = 64 [using (i)]
⇒ a2 – 20a + 64 = 0
⇒ (a – 4)(a – 16) = 0
⇒ a = 4, 16
Taking a = 4, we get b = 20 – 4 = 16
Taking a = 16, we get b = 20 – 16 = 4
Thus, the two numbers are 4, 16, or 16, 4
OR
Given, \(\frac{a_7}{a_{10}}=\frac{5}{7}\)
Let the first term and common difference of A.P be ‘A’ and ‘D’ respectively.
∴ \(\frac{A+6 D}{A+9 D}=\frac{5}{7}\)
⇒ 7A + 42D = 5A + 45D
⇒ 2A = 3D
⇒ A = \(\frac{3}{2}\)D …..(i)
Now, \(\frac{a_4}{a_7}=\frac{A+3 D}{A+6 D}\)
= \(\frac{\frac{3}{2} D+3 D}{\frac{3}{2} D+6 D}\)
= \(\frac{9 D}{15 D}\) [using (i)]
= \(\frac{3}{5}\)

Question 27.
If ‘men are very busy’ means, ‘1234’, ‘Busy person need encouragement’ means ‘4567’, ‘encouragement is very important’ means ‘3589’ and ‘Important persons are rare’ means, ‘2680’, then
(i) What is the code for ‘encouragement’?
(ii) According to given code, what is the code of ‘Men need encouragement’?
Answer:
Given statements and their codes are as follows:
(I) Men are very busy ⇒ 1 2 3 4
(II) Busy persons need encouragement ⇒ 4 5 6 7
(III) Encouragement is very important ⇒ 3 5 8 9
(IV) Important persons are rare ⇒ 2 6 8 0
(i) In second (II) and third (III) sentences, common word is ‘encouragement and common code no. is ‘5’. Hence, number 5 stands for encouragement. 1
(ii) In first (I) and fourth (IV) sentences, the common word is ‘are’, hence ‘are’ stands for ‘2’ from first (I) and third (III) sentences, ‘very’ stand for ‘3’ from first (I) and second (II) sentences, ‘busy’ stands for ‘4’. Hence, we get from first sentence ‘Men stand for ‘1’ similarly ‘needs’ stand for ‘7’. From this, we conclude that ‘Men need encouragement’ will be coded as ‘1 5 7’.

Question 28.
Find the domain and range of f(x) = |2x – 3| – 3.
Answer:
Given, f(x) = |2x – 3| – 3
The domain of the expression is all real number except where the expression is undefined. In this case, there is no real number that makes the expression undefined.
∴ Domain of f = (-∞, ∞) = R

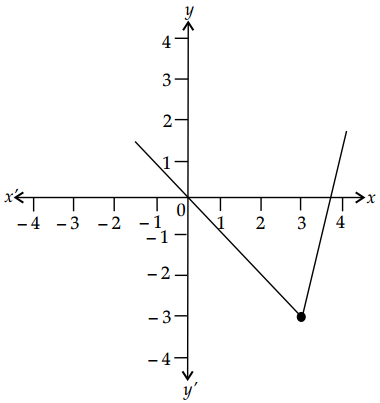
The absolute value of expression has a ‘V’ shape.
The range of a positive absolute value expression starts at its vertex and extends to infinity.
Range of f = [-3, ∞) or {y : y ≥ -3}

Question 29.
The mean and S.D. for a, b and 2 are 3 and 2√3, respectively. Find value of ab.
Answer:
Given, mean = 3
S.D. = 2√3
Given numbers are a, b, and 2
∴ mean = \(\frac{a+b+2}{3}\)
⇒ a + b + 2 = 9
⇒ a + b = 7 …….(i)
Standard Deviation = \(\sqrt{\frac{\Sigma(x-\text { mean })^2}{n}}\) [∵ n = 3]
2√3 = \(\sqrt{\frac{\Sigma(x-\text { mean })^2}{3}}\)
Squaring both sides, we get
12 = \(\frac{\Sigma(x-\text { mean })^2}{3}\)
⇒ 36 = Σ(x – mean)²
Now, Σ(x – mean)² = (a – 3)² + (b – 3)² + (2 – 3)²
⇒ 36 = (a² + 9 – 6a) + (b² + 9 – 6b) + 1
⇒ 36 = a² + b² – 6(a + b) + 19
Using (a + b)² = a² + b² + 2ab
⇒ 36 = (a + b)² – 2ab – 6(a + b) + 19
⇒ 36 = (7)² – 2ab – 6(7) + 19
⇒ 2ab = 49 – 42 + 19 – 36
⇒ 2ab = 68 – 78
⇒ ab = -5

Question 30.
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
OR
Find the equation of a circle having (1, -2) as its centre and passing through intersection of lines 3x + y = 14 and 2x + 5y = 18.
Answer:
Let the image of point P(3, 8) be Q(a, b) with respect to line AB which is given by
x + 3y – 7 = 0 ……(i)
The mid-point of P and Q is \(\left(\frac{3+a}{2}, \frac{8+b}{2}\right)\), which lies on line (i).
From (i), \(\frac{3+a}{2}+3 \cdot \frac{8+b}{2}-7\) = 0
⇒ 3 + a + 24 + 3b – 14 = 0
⇒ a + 3b + 13 = 0 ……(ii)
Now, slope of AB = \(-\frac{1}{3}\)
and slope of PQ = \(\frac{b-8}{a-3}\)
∴ \(-\frac{1}{3} \times \frac{b-8}{a-3}\) = -1
⇒ 3a – b – 1 = 0 ……(iii)
Solving (ii) and (iii), we arrive at a = -1, b = -4
∴ Image of (3, 8) is (-1, -4).
OR
Given lines are
3x + y = 14 ……(i)
and 2x + 5y = 18 …….(ii)
On solving equations (i) and (ii), we get
x = 4 and y = 2
Therefore, the point of intersection say P, of given lines is (4, 2)
Since, the centre of the circle is (1, -2) and it passes through the point (4, 2),
so its radius, CP = \(\sqrt{(4-1)^2+\{2-(-2)\}^2}\) = 5 units
Thus, required equation of circle is (x – 1)² + {y – (-2)}² = (5)²
⇒ (x² – 2x + 1) + (y² + 4y + 4) = 25
⇒ x²y² – 2x + 4y – 20 = 0

Question 31.
Let Amar, Ram and Rahim be three dealers belonging to different states. Dealer Amar sells some products/services to dealer Ram for ₹ 1000 dealer Rahim at a profit of ₹ 300. Calculate the tax liability of Ram, if the rate of GST is 12%.
Answer:
For dealer Amar,
Selling price = ₹ 1000 [Given]
∵ Since in case of inter-state, we get
IGST = ₹ \(\frac{12}{100}\) × 1000 = ₹ 120
For dealer Ram,
Cost price = ₹ 1000
∴ Selling price = ₹ (1000 + 300) = ₹ 1300
For dealer Rahim,
Cost price = ₹ 1000
Profit = ₹ 300
Input tax credit = ₹ 120
Output tax = ₹(\(\frac{12}{100}\) × 1300) = ₹ 156
∴ Tax liability on dealer Ram = ₹(156 – 120) = ₹ 36

Section-D

(This section comprises long answer type questions (LA) of 5 marks each)

Question 32.
In an A.P., if the p^th term is pth and q^th term is \(\frac{1}{p}\). Prove that the sum of first pq term is \(\frac{1}{2}\)(pq + 1).
Answer:
∵ T_n = a + (n – 1)d
Therefore, T_p = a + (p – 1)d = \(\frac{1}{q}\) [given] ……(i)
a + (q – 1) = \(\frac{1}{p}\) [given] ……(ii)
Subtracting Equation (i) from Equation (ii),
d(p – 1 – q + 1) = \(\frac{1}{q}-\frac{1}{p}\)
⇒ d(p – q) = \(\frac{p-q}{p q}\)
⇒ d = \(\frac{1}{pq}\)
Putting the value of d in Equation (i), we get

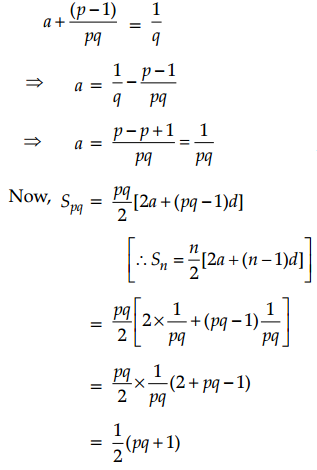
Question 33.
If x^y = e^x-y, prove that \(\frac{d y}{d x}=\frac{\log x}{(\log x e)^2}\).
Answer:
x^y = e^x-y
taking logarithms bothsides
⇒ log x^y = log e^x-y
⇒ y log x = (x – y) log e = x – y
⇒ y log x + y = x
⇒ y(1 + log x) = x


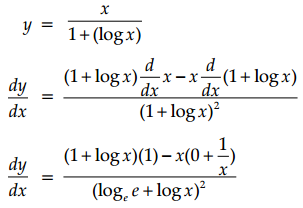
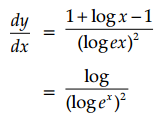
Hence Proved.

Question 34.
A girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1, 2, 3, or 4, she tosses a coin two times and notes the number of heads obtained. If she obtained exactly two heads, what is the probability that she threw 1, 2, 3, or 4 with the die?
OR
An insurance company insured 1500 scooter drivers, 2500 car drivers and 4500 truck drivers. The probability of a scooter, a car and a truck meeting with an accident is 0.01, 0.02 and 0.04 respectively. If one of the insured persons meets with an accident, find the probability that he is a scooter driver.
Answer:
When a die is thrown,
Sample space = {1, 2, 3, 4, 5, 6}
Let E₁: Girl get 5 or 6
E₂: Girl gets 1, 2, 3, or 4
Then, P(E₁) = \(\frac{2}{6}=\frac{1}{3}\)
and P(E₂) = \(\frac{4}{6}=\frac{2}{3}\)
When she gets 5 or 6, she throws a coin three times.
Sample Space = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Out of these 8 outcomes, exactly two heads are obtained in the 3 outcomes.
i.e., HHH, HHT, THH.
If A denotes the event of getting exactly two heads, then
∴ \(P\left(\frac{A}{E_1}\right)=\frac{3}{8}\)
Again, when she gets 1, 2, 3 or 4 she throws a coin two times.
Sample space = {HH, HT, TH, TT}
∴ \(P\left(\frac{A}{E_2}\right)=\frac{1}{4}\)
Thus, by Bayes’ theorem, we have probability that girl gets exactly two heads, when she threw 1, 2, 3 or 4 with the die

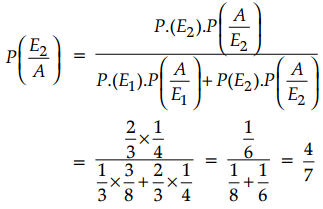
OR
Let E₁, E₂ and E₃ be event of insured driver of scooter, car and truck, respectively.
Then, P(E₁) = \(\frac{1500}{8500}=\frac{15}{85}=\frac{3}{17}\)
P(E₂) = \(\frac{2500}{8500}=\frac{5}{17}\)
and P(E₃) = \(\frac{4500}{8500}=\frac{9}{17}\)
Now, probability that scooter driver meets with an accident.
\(P\left(\frac{A}{E_1}\right)\) = 0.01
Probability that car driver meets with an accident
\(P\left(\frac{A}{E_2}\right)\) = 0.02
Probability that truck driver meets with an accident
\(P\left(\frac{A}{E_3}\right)\) = 0.04
The probability that scooter driver meets with an accident,

Question 35.
Find the quartile deviation and its coefficient for the marks obtained by 10 students:
56, 48, 65, 35, 42, 75, 82, 60, 55
OR
An analysis of monthly wages paid to workers in two firms A and B, belonging to the same industry, gives the following results:

Particulars	Firm A	Firm B
No. of Wage Earners	586	648
Mean of Monthly Wages	₹ 5253	₹ 5253
Variance of the Distribution of Wages	100	121

(i) Which firm A or B pays larger amounts as monthly wages?
(ii) Which firm A or B shows greater variability in individual wages?
Answer:
After arranging the marks in an ascending order:
35, 42, 48, 50, 55, 56, 60, 65, 75, 82
First quartile, Q₁ = \(\left(\frac{n+1}{4}\right)^{\mathrm{th}}\) observation
= \(\left(\frac{10+1}{4}\right)^{\mathrm{th}}\) observation
= 2.75th observation
= 2nd observation + 0.75 × (difference between the third and the 2nd observation)
= 42 + 0.75 × (48 – 42)
= 46.50
Third quartile, Q₃ = \(\frac{3(n+1)}{4}^{\text {th }}\) observation
= \(\frac{3(10+1)}{4}^{\text {th }}\) observation
= 8.25th observation
= 65 + 0.25 × (difference between 9th and 8th observations)
= 65 + 0.25 × 10
= 65 + 2.5
= 67.50
Quartile Deviation = \(\frac{Q_3-Q_1}{2}\)
= \(\frac{67.50-46.50}{2}\)
= 10.50
OR
For Firm A:
No. of wages earners = 586
Mean of monthly wages, \(\bar{x}\) = ₹ 5253
Amount paid by firm A = ₹(586 × 5253) = ₹ 3078258
Variance of distribution of wages, σ² = 100
Standard deviation, σ = \(\sqrt{100}\) = 10
Coefficient of Variation = \(\frac{\sigma}{\bar{x}} \times 100\)
= \(\frac{10}{5253}\) × 100
= 0.19
For Firm B:
No. of wage earners = 648
Mean of monthly wages, \(\bar{x}\) = ₹ 5253
Amount paid by firm B = ₹(648 × 5253) = ₹ 3403944
Standard deviation, σ = \(\sqrt{121}\) = 11
Coefficient of variation = \(\frac{\sigma}{\bar{x}} \times 100\)
= \(\frac{11}{5253}\) × 100
= 0.21
Monthly wages paid by firm A = ₹ 3078258
Monthly wages paid by firm B = ₹ 3403944
∴ Firm B pays larger amount as monthly wages.
Coefficient of variation of wages, of firm A = 0.19
Coefficient of variation of wages, of firm B = 0.21
∴ Firm B shows greater variability in individual wages.

Section-E

(This section comprises 3 source-based questions (Case Studies) of 4 marks each)

Question 36.
Two friends Saurabh and Manoj were playing cards. There were 52 cards in a deck.

On the basis of this information answer the following questions:
(i) In how many ways Saurabh can select all four cards from same suit?
(ii) In how many ways Manoj can select four cards from different suits?
OR
In how many ways Saurabh can select all face cards?
(iii) In how many Saurabh select two red and two black cards?
In how many ways Manoj can select two cards of same colour?
Answer:
(i) Saurabh can choose four cards from same suit in 4 × ¹³C₄ ways.
= 4 × \(\frac{13 !}{9 ! \times 4 !}\)
= 2860
(ii) Here one card to be selected from each suit therefore, he can select in ¹³C₁ × ¹³C₁ × ¹³C₁ × ¹³C₁ ways.
= (¹³C₁)⁴
= (13)⁴
OR
There are 12 face cards and 4 are to be selected out of these 12 cards.
This can be done in ¹²C4 ways = \(\frac{12 !}{8 ! 4 !}\) = 495
(iii) Two red and two black cards can be selected in ²⁶C₂ × ²⁶C₂ ways.
= \(\left(\frac{26 !}{24 ! 2 !}\right)^2\)
=105625
Manoj can select two cards of same colour in ²⁶C₂ + ²⁶C₂ ways.
= 325 + 325
= 650 ways

Question 37.
In XI standard, teacher was discussing the concept of Future Value of Annuity Regular. During his class, he discussed the following few points on this: ₹ 500 was invested in annuity (future value regular) for 10 years at the rate of 14% compounded annually.

On the basis of the above information, answer the following questions:
If C.F. be the periodic payments, (cash flow in each period), the future value F.V. (n, i) of the annuity is given by:
Future value (F.V.) of an Annuity = C.F. \(\left[\frac{(1+i)^n-1}{i}\right]\)
(i) What will be the future value of annuity at the end of two years? Given that (1.14)² = 1.2996.
OR
What will be the future value of the annuity after 3 years? Given that (1.14)³ = 1.4815.
(ii) Give four examples of regular annuity.
(iii) What is the approximate value of the annuity for five years? Given that (1.14)⁵ = 1.925.
Answer:
(i) By using the formula,
F.V of an Annuity = C.F. \(\left[\frac{(1+i)^n-1}{i}\right]\)
Here, C.F. = 500, i = 0.14, n = 2
By putting these values, we get:
F.V of an Annuity at the end of two years = \(500\left[\frac{(1+0.14)^2-1}{0.14}\right]\)
= \(\frac{0.2996}{0.14}\) × 500
= 500 × 2.14
= 1070
OR
After three years future value of an annuity

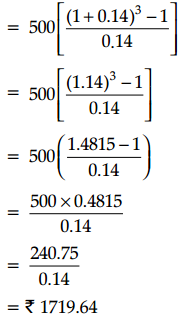
(ii) Examples of regular annuity are:
(a) Deposits to a saving account with regular period of time of a fixed payment.
(b) Monthly insurance payments
(c) Pension payments
(d) Monthly rent of a house
(iii) After five years future value of the annuity

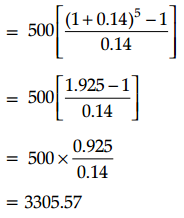
Question 38.
The binary number system, also referred to base 2, makes use of only two digits i.e., 1 and 0. ‘Bi’ in binary is analogous to bi bicycle (two wheels). Each digit of the binary system called a bit originating from binary digit.
Conversion of Binary to Decimal: Since, binary number system has base 2, the positional values are computed in terms of powers of 2.
Conversion of Decimal to Binary: To convert a decimal number into binary number, we divide decimal number repeatedly by 2 because the base value of binary system is 2. Record the remainder after each division and finally write the remainders in reverse order in which they computed.
(i) Convert the following binary numbers to their decimal representation.
(a) (101010)₂
(b) (111.10101)₂
OR
(ii) Convert (0.675)₁₀ to binary.
Answer:
(i) (a) Given, binary number is 101010

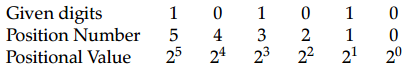
Decimal Number = 1 × 2⁵ + 0 × 2⁴ + 1 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰
= 32 + 0 + 8 + 0 + 2 + 0
= 42
Thus, (101010)₂ = (42)₁₀
(b) Given digits
1 1 1 . 1 0 1 0 1
Fractional Value
2² 2¹ 2⁰ . 2^-1 2^-2 2^-3 2^-4 2^-5
Decimal Value = 1 × 2² 1 × 2¹ 1 × 2⁰ . 1 × 2^-1 0 × 2^-2 1 × 2^-3 0 × 2^-4 1 × 2^-5
= 4 + 2 + 1 . 0.5 + 0 + 0.125 + 0 + 0.03125
= 7.65625
Thus, (111.10101)₂ = (7.65625)₁₀
OR
(ii)

Since the fraction part (0.400) is the repeating value in the calculation, the multiplication is stopped.
Now, we have to write the integral part from top to bottom to get binary number for the given fraction part.
Therefore, (0.675)₁₀ = (0.1010110)₂