Students can access the CBSE Sample Papers for Class 10 Maths Standard with Solutions and marking scheme Set 5 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Standard Set 5 with Solutions
Time: 3 Hours
Maximum Marks: 80
General Instructions:
- This Question Paper has 5 Sections A, B, C, D and E.
- Section A has 20 MCQs carrying 1 mark each
- Section B has 5 questions carrying 02 marks each.
- Section C has 6 questions carrying 03 marks each.
- Section D has 4 questions carrying 05 marks each.
- Section E has 3 case based integrated units of assessment (04 marks each) with sub parts of the values of 1, 1 and 2 marks each respectively.
- All Questions are compulsory. However, an internal choice in 2. Qs of 5 marks, 2.Qs of 3 marks and 2. Questions of 2 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
- Draw neat figures wherever required. Take n = 22/7 wherever required if not stated.
Section – A ( 20 Marks)
Section A Consists of Multiple Choice Type questions of 1 mark each
Question 1.
Let p and q be two natural numbers such that p > q. When p is divided by q, then remainder is r.
(i) r CANNOT be (p -q).
(ii) r CAN either be q or (p -q).
(iii) r is DEFINITELY less than q.
Which of the above statements is/are true?
(A) only (ii)
(B) only (iii)
(C) only (i) and (iii)
(D) cannot be determined without knowing the values of p, q and r
Solution:
(B) only (iii)
Explanation: q is divisor and r is remainder
∴ r is less than q.
![]()
Question 2.
The graph of a polynomial p(x) cuts the X-axis at 3 points and touches it at 2 other points. The number of zeroes of p(x) is
(A) 1
(B) 2
(C) 3
(D) 5
Solution:
(D) 5
Explanation: According to the property of the polynomials,
Number of zeroes = Number of points at which graph intersects the X-axis.
According to given condition, the graph intersects the X-axis at 5 different points.
Therefore, number of zeroes = 5.
Question 3.
If the discriminant of the equation 6x2 – bx + 2 = 0 is 1, then value of b is:
(A) 7
(B) -7
(C) ±7
(D) None of these
Solution:
(C) ±7
Explanation: Given equation, 6x2 – bx + 2 = 0
On comparing with Ax2 + Bx + C = 0, we get A = 6, B= -b and C = 2
Now, Discriminant = B2 – 4AC
⇒ 1 = (0) – 4 × 6 × 2
⇒ 1 = b2 – 48
⇒ b2 = 49
⇒ b = ±7
Question 4.
What is the value of q if \(\frac{p}{2}\) + 3q = 6 and 2p – 2q = 10?
(A) 1
(B) 4
(C) 6
(D) 16
Solution:
(A) 1
Explanation: Given,
\(\frac{p}{2}\) + 3q = 6
⇒ p + 6q = 12 … (i)
and 2p – 2q = 10
or, p – q = 5 … (ii)
Subtracting eq.(ii) from eq.(i), we get
7q = 7 ⇒ q = 1
Question 5.
If 7 times the 7th term of an A.P. is equal to 11 times its 11th term, then its 18th term will be:
(A) 7
(B) 11
(C) 18
(D) 0
Solution:
(D) 0
Explanation: According to question,
7t7 = 11t11
= 7(a + 6d) = 11(a + 10d)
⇒ 4a + 68d = 0
⇒ 4(a + 17d) = 0
⇒ (a + 17d) = 0
⇒ t18 = 0
Question 6.
The distance of the point (20, 15) from origin is:
(A) 15 units
(B) 20 units
(C) 25 units
(D) 30 units
Solution:
(C) 25 units
Explanation: Given points are P(20, 15) and origin 0(0,0)
∴ Distance between two points, OP
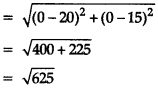
= 25 units
![]()
Question 7.
In what ratio, does the point (-4, 6) divide the line segment joining the points A(-6, 10) and B(3, -8)?
(A) 2:7
(B) 7:2
(C) 1:2
(D) 2:1
Solution:
(A) 2:7
Explanation:

∴ Required ratio is 2:7.
Question 8.
The area of the circle that can be inscribed in a square of side 3 cm is:
(A) \(\frac{3 \pi}{2}\) cm2
(B) \(\frac{5 \pi}{2}\) cm2
(C) \(\frac{7 \pi}{2}\) cm2
(D) \(\frac{9 \pi}{2}\) cm2
Solution:
(D) \(\frac{9 \pi}{2}\) cm2
Explanation:
Given, Side of square = 3 cm
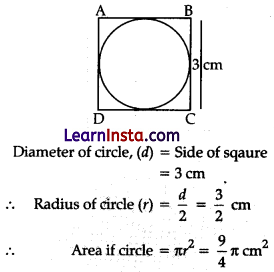
Question 9.
In the given figure, if TP and TQ are the two tangents to a circle with centre O such that ∠POQ = 110°, then ∠PTQ is equal to:
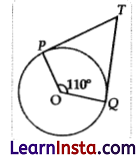
(A) 60°
(B) 70°
(C) 80°
(D) 90°
Solution:
(B) 70°
Explanation: Given that, TP and TQ are tangents.
Since, the radius drawn to the tangents will be perpendicular on it.
∴ OP ⊥ TP and OQ ⊥ TQ

∠OPT = 90° and ∠OQT = 90°
In quadrilateral POQT,
Sum of all interior angles = 360°
∠OPT + ∠POQ + ∠OQT + ∠PTQ =360°
90° + 110° + 90° + ∠PTQ = 360°
∠PTQ = 70°
![]()
Question 10.
If the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then:
(A) R1 + R2 = R
(B) R1 + R2 > R
(C) R1 + R2 < R
(D) Nothing definite can be said about the relation among R1, R2 and R.
Solution:
(A) R1 + R2 = R
Explanation: According to question,
Circumference of circle = circumference of first circle + circumference of second circle
2πR = 2πR1 + 2πR2
R = R1 + R2
Question 11.
sec θ when expressed in terms of cot θ, is equal to:
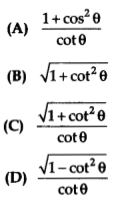
Solution:
(C) \(\frac{\sqrt{1+\cot ^2 \theta}}{\cot \theta}\)
Explanation:

[∵ cosec2 θ ∵ = 1 + cot2 θ]
Question 12.
If tan(6x + 30°) = 1, then x is
(A) 15°
(B) 5°
(C) 3°
(D) None of these
Solution:
(C) 3°
Explanation: Given,
tan(5x + 30°) = 1
or, tan(5x + 30°) = tan 45°
or, 5x + 30° = 45°
or, 5x = 15°
or, x = 3°
Question 13.
If sin A = \(\frac{12}{13}\), the value of cos A is :
(A) \(\frac{13}{4}\)
(B) \(\frac{13}{5}\)
(C) \(\frac{5}{13}\)
(D) \(\frac{4}{13}\)
Solution:
(C) \(\frac{5}{13}\)
Explanation:

![]()
Question 14.
“If k + 2, 4k – 6 and 3k – 2 are three consecutive terms of A.P. then the value of k is:
(A) 3
(B) -3
(C) 4
(D) 4
Solution:
(A) 3
Explanation: Since, 1 + 2, 41 – 6 and 3k – 2 are
consective terms of A.P.
∴ (4k – 6) – (k + 2) = (3k – 2) – (4k – 6)
3k – 8 = -k + 4
4k = 12
k = 3
Question 15.
If the sum of the first n terms of an A.P. be 3n2 + n and its common difference is 6, then its first term is:
(A) 2
(B) 3
(C) 1
(D) 4
Solution:
(D) 4
Explanation: Sn = 3n2 + n
According to formula,
Sn = \(\frac{n}{2}\)[2a + (n – 1)d]
3n2 + n = \(\frac{n}{2}\)[2a + 6n – 6]
6n2 + 2n = 2an + 6n2 – 6n
\(\frac{8n}{2n}\) = a
∴ a = 4
Thus, first term = 4
Question 16.
For an event E, P(E) + P(Ē) = x, then the value of x3 – 3 is:
(A) -2
(B) 2
(C) 1
(D) -1
Solution:
(A) -2
Explanation: Given
P(E) + P(Ē) = x …(i)
Also, according to the law of probability,
P(E) + P(Ē) = 1 … (ii)
From (i) and (ii), we get
x = 1
Put value of x in x3 – 3, we get
x3 – 3 = (1)3 – 3 = 1 – 3 = -2
Question 17.
Look at the numbers shown below:
(i) -0.5
(ii) 0.00001
(iii) \(\frac{1}{2}\)
(iv) 1
(v) 1.00001
(vi) 99%
Which of the above numbers represent probabilities of events?
(A) only (i) and (iii)
(B) only (i), (ii), (iii) and (iv)
(C) only (ii), (ii), (iv) and (v)
(D) only (ii), (ii), (iv) and (vi)
Solution:
(D) only (ii), (ii), (iv) and (vi)
Explanation: Since, we know that the probability can neither be negative nor be greater than one.
So, -0.5 arid 1.00001 can not represent probabilities of events.
Hence, only (ii), (iii), (iv) and (vi) represent probabilities of events.
![]()
Question 18.
The empirical relation between the mode, median and mean of a distribution is:
(A) Mode = 3 Median – 2 Mean
(B) Mode = 3 Mean – 2 Median
(C) Mode = 2 Median – 3 Mean
(D) Mode = 2 Mean – 3 Median
Solution:
(A) Mode = 3 Median – 2 Mean
Explanation: Empirical formula
Mode = 3 Median – 2 Mean
DIRECTIONS: Two statements are given below – one labelled Assertion (A) and the other labelled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).
(A) Both (A) and (R) are true and (R) is the correct explanation of the (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation of the (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Question 19.
Assertion (A): The area of a quadrant of a circle whose circumference is 22 cm is \(\frac{77}{8}\) cm2
Reason (R): Area of a quadrant of a circle with radius, r is = \(\frac{\pi r^2}{4}\).
Solution:
(A) Both (A) and (R) are true and (R) is the correct explanation of the (A).
Explanation: Given circumference of a circle = 22 cm
2πr = 22

Question 20.
Assertion (A): If the sum of first n terms of an AP is given by Sn = 6n + 7n2, then its nth term is 7n2 – 8n + 1.
Reason (R): nth term can use obtained using formula an = Sn – Sn-1.
Solution:
(D) (A) is false but (R) is true.
Explanation: We have,
Sn = 6n + 7n2
Sn-1 = 6(n – 1) + 7(n – 1)2
= 6n – 6 + 7(n2 – 2n + 1)
= 6n – 6 + 7n2 – 14n + 7
= 7n2 – 8n + 1
an = Sn – Sn-1
an = (7n2 + 6n) (7n2 – 8n + 1)
= 7n2 + 6n – 7n2 + 8n – 1
= 14n – 1
So assertion is false and reason is true.
Section – B (10 Marks)
Section B consists of 5 questions of 2 marks each
Question 21.
Given that √2 is irrational, prove that (5+3√2) is an irrational number.
Solution:
Given that √2 is irrational number.
Let, 5 + 3√2 be rational.
So 5 + 3√2 = \(\frac{p}{q}\),
where′a′and′b′are integers and q ≠ 0
3√2 = \(\frac{p}{q}\) – 5
√2 = \(\frac{p-5q}{3q}\)
Since ‘a’ and ‘b’ are integers p – 5q is also an integer \(\frac{p-5q}{3q}\) is rational. So RHS is rational.
√2 is irrational number.
So, our supposition is wrong.
So 5 + 3√2 is an irrational number.
Question 22.
In the given figure, if ∠A = 90, ∠B = 90, OB = 45cm, OA = 6 cm and AP = 4 cm, then find QB.
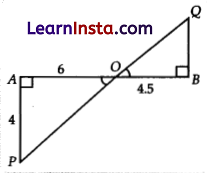
Solution:
In APAO and AQBO,
∠A = ∠B = 90° (Given)
∠POA = ∠QOB (vertically opposite angles)
Since, ΔPAO ∼ ΔQBO, (by AA)

∴ QB = 3 cm
![]()
Question 23.
Find the number of natural numbers between 102 and 998 which are divisible 45 by 2 and 5 both.
Solution:
The number which ends with 0 is divisible by 2 and 5 both.
∴ Such numbers between 102 and 998 are:
110, 120,130, ……., 990.
Last term, an = 990
a + (n – 1)d =990
110 + (n – 1) × 10 = 990
110 + 10n -10 = 990
10n + 100 = 990
10n = 990 – 100
10n = 890
n = \(\frac{890}{10}\) = 89
n = 89
Question 24.
If tan θ = \(\frac{1}{\sqrt{5}}\)
(A) Evaluate: \(\frac{{cosec}^2 \theta-\sec ^2 \theta}{{cosec}^2 \theta+\sec ^2 \theta}\)
Solution:

OR
(B) Verify the identity: sin2 θ + cos2 θ = 1.
Solution:

Question 25.
(A) Show below are two overlapping sectors of a circle. The radii of the sectors are 6 cm and 8 cm. The figure is divided into three regions -I, II and III
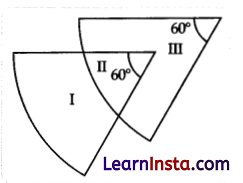
(Note: The figure is not to scale)
Find the difference in the areas of regions I and III. Show your work.
(Note: Take π = \(\frac{22}{7}\))
Solution:
Let radius of sector (I + II) = 8 cm
And radius of setor (II + III) = 6 cm

![]()
OR
(B) The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
Solution:
We know that, in 60 minutes, the tip of minute hand moves 360°
In 1 minute, it will move = \(\frac{360°}{60}\) = 60°
∴ From 7: 05 p.m. to 7: 40 p.m. i.e., 35 min, it will move through = 35 × 6° = 210°
∴ Area swept by the minute hand in 35 min = Area of sector with sectorial
angle 210° and radius of 6 cm
= \(\frac{210°}{360°}\) × π × 62
= \(\frac{7}{12}\) × \(\frac{22}{7}\) × 36
= 66 cm2
Section – C (18 Marks)
Section C Consists of 6 questions of 3 marks each
Question 26.
Find the greatest number of six digits exactly divisible by 18, 24 and 36.
Solution:
LCM of 18, 24 and 36
18 = 2 × 32
24 = 23 × 3
36 = 22 × 32
LCM (18, 24, 36) = 23 × 32
= 72
The largest 6 digit number is 999999

∴ The required number = 999999 – 63 = 999936.
Question 27.
f(x) = x3 – ax2 + (a – 3)x + 6, where a is a non-zero real number. When f(x) is divided by (x + 1), there is no remainder.
If f(x) is completely factorable, find the zeroes of f(x). Show your steps.
Solution:
Since,f(x) is divisible by (x + 1)
∴ f(-1) = 0
Thus f(-1) = (-1)3 – a(-1)2 + (a – 3) – 1 + 6 = 0
– 1 – a – a + 3 + 6 = 0
8 – 2a = 0
8 = 2a
a = 4
After substituting value of ‘a’ we get
f(x) = x3 – 4x2 + x + 6

On factorising x2 – 5x + 6, we get
= x2 – 3x – 2x + 6
= x(x – 3) -2 (x – 3)
= (x – 3)(x – 2)
x = 3 and x = 2
Thus, zeroes of f(x) are (-1), 2 and 3.
Question 28.
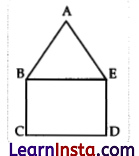
(A) In the figure, ABCDE is a pentagon with BE||CD and BC||DE. BC is perpendicular to CD.
AE = AB = 5m, BE = 7 cm, BC = x – y and CD = x + y. If the perimeter of ABCDE is 27 cm. find the value of x and y, given x, y # 0.
Solution:
Here, BCDE is a rectangle
∴ x + y = 7 … (i)
Perimeter of ABCDE = 27 cm (given)
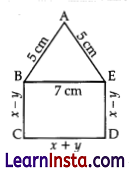
∴ AB + BC + CD + DE + EA = 27
⇒ 3x – y = 27 – 10
⇒ 3x – y = 17 … (ii)
Adding eq. (i) and (ii), we get
4x = 24
x = 6
Substituting the value of x in e.q. (i), we get
6 + y = 7
y = 7 – 6 = 1
Hence, x = 6 and y = 1.
![]()
OR
(B) Determine graphically the co-ordinates of the vertices of triangle, the equations of whose sides are given by 2y – x = 8, 5y – x = 14 and y – 2x = 1.
Solution:
Given, 2y – x = 8
⇒ x = 2y – 8
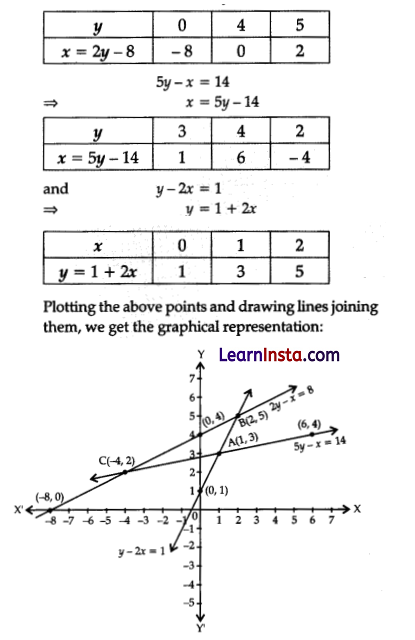
Hence, the co-ordinates of the vertices of the triangle ABC are A(1, 3), B(2, 5) and C(-4, 2).
Question 29.
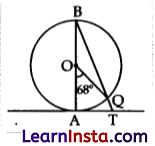
(A) In given figure, AB is the diameter of a circle with centre O and AT is a tangent ∠AOQ = 68°, find ∠ATQ.
Solution:
∠AOQ = 68° (Given)
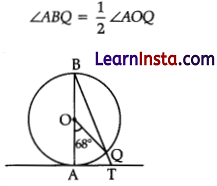
[Angle on the circumference of the circle by the same arc]
= \(\frac{1}{2}\) × 68°
= 34°
∠BAT = 90° [∵ OA ⊥ AT]
∠ATQ = 90° – 34°
= 56°
OR
(B) Ifacircle touches the side BC of a triangle ABC at P and extended sides AB and AC at Q and R, respectively.
prove that AQ = \(\frac{1}{2}\)(BC + CA + AB)
Solution:
BC + CA + AB
= (BP + PQ + (AR – CR) + (AQ – BQ)
= AQ + AR – BQ + BP + PC – CR
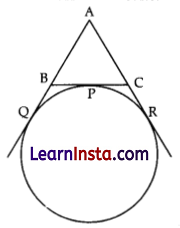
From the same external point, the tangent segments drawn to a circle are equal.
From the point B, BQ = BP
From the point A, AQ = AR
From the point C, CP = CR
Perimeter of AABC,
AB + BC + CA = 2AQ – BQ + BQ + CR – CR
⇒ = 2AQ
⇒ AQ = \(\frac{1}{2}\)(BC + CA + AB)
![]()
Question 30.
If tan (A + B) = 1 and tan (A – B) = \(\frac{1}{\sqrt{3}}\), 0° < A + B < 90°, A > B, then find the values of A and B.
Solution:
tan (A + B) = 1
⇒ tan(A + B) = tan 45°
⇒ A + B = 45° ……….(1)
tan(A – B) = \(\frac{1}{\sqrt{3}}\)
⇒ tan (A – B) = tan 30°
⇒ A – B = 30 ……(2)
On adding (1) and (2), we obtain
2A = 75°
⇒ A = 37.5°
Putting the value of A in (1) we get
37.5° + B = 45°
⇒ B = 7.5°
Therefore,∠A = 37.5° and ∠B = 7.5°
Question 31.
The frequency distribution of daily rainfall in a town during a certain period is shown below.
| Rainfall (in mm) | Number of days |
| 0 – 20 | 10 |
| 20 – 40 | x |
| 40 – 60 | 12 |
| 60 – 80 | 8 |
Unfortunately, due to manual errors, the information on the 20-40 mm range got deleted from the data.
If the mean daily rainfall for the period was 32 mm, find the number of days when the rainfall ranged between 20-40 mm. Show your work.
Solution:
| Rainfall (in mm) | Number of days frequency (fi) | Class Marks(xi) | (fixi) |
| 0 – 20 | 10 | 10 | 100 |
| 20 – 40 | x | 30 | 30x |
| 40 – 60 | 12 | 50 | 600 |
| 60 – 80 | 8 | 70 | 560 |
| Total | 30 + x | 1260 + 30x |
Mean = 32 mm (Given)
And, Mean = \(\frac{1260+30 x}{30+x}\)
32 = \(\frac{1260+30 x}{30+x}\)
960 + 32x = 1260 + 30x
2x = 300
x = 150
Hence, number of days are 23.
Section – D (20 Marks)
Section D consists of 4 questions of 5 marks each
Question 32.
(A) Seven times a two digit number is equal to four times the number obtained by reversing the order of its digits. If the difference of the digits is 3, determine the number.
Solution:
Let the ten’s and unit digit be y and x respectively.
So, the number is 10y + x.
The number, when its digits are reversed, becomes 10x + y
So, 7(10y + x) = 4(10x + y)
70y + 7x = 40x + 4y
70y – 4y = 40x – 7x
2y = x … (i)
and x – y = 3 … (ii)
From (i) and (ii), we get
y = 3 and x = 6
Hence, the number is 36.
OR
(B) One says, ‘Give me a hundred, friend! I shall then became twice as rich as you’. The other replies, ‘If you give me ten, I shall be six times as rich a you’. Tell me what is the amount of their (respective) capital?
Solution:
Let the amount of their respective capital be ₹x an ₹y.
According to question,
x + 100 = 2(y – 100)
⇒ x – 2y = -300 … (i)
and 6(x – 10) = y + 10
⇒ 6x – y = 70 … (ii)
On multiplying eqn. (ii) by 2 and than subtracting from eqn. (i) we get
x – 12x = -300 -1 40
⇒ -11x = -440
On substituting the value of* in eqn. (i), we get
40 – 2y = -300
⇒ -2y = -340
⇒ y = 170
Hence, the amount of there respective caitals are ₹40 and ₹170.
![]()
Question 33.
In the given figure, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD × AD.
Solution:
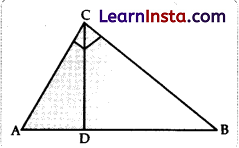
In ΔACB and ΔADC
∠C = ∠D (both 90°)
∠A = ∠A (common)
∴ ΔACB ~ ΔADC (AA similarity)

Question 34.

(A) A right cylindrical container of radius 6 cm and height 15 cm is full of
ice-cream, which has to be distributed to 10 children in equal cones having hemispherical shape on the top. If the height of the conical portion is four times its base radius, find the radius of the ice-cream cone.
Solution:
Volume of ice-cream in the cylinder = π(6)2 × 15 cm3
Volume of ice-cream in one cone = \(\frac{1}{3}\)πr2 × 4r + \(\frac{2}{3}\)πr3 (Given, h = 4r)
= 2πr3 cm3
⇒ 10(2πr3) = π(6)2 × 15
⇒ r3 = 33
⇒ r = 3 cm
So the radius of ice-cream cone is 3 cm.
Detailed Answer:
Given, radius of right cylinder (r) = 6 cm
height of right cylinder (h) = 15 cm
Volume of ice-cream in the cylinder (V1) = πr2h1
= π(6)2 × 15
= 540π cm3
Also given, height of the conical portion is four times its base radius i.e., height of cone, h = 4r
∴ Volume of ice-cream in one cone = Volume of cone + volume of hemispherical shape on the top
= \(\frac{1}{3}\)πr2h + \(\frac{2}{3}\)πr3
= \(\frac{1}{3}\)πr2 × 4r + \(\frac{2}{3}\)πr3
= 2πr3 cm3 [∵ h = 4r]
Now, volume of ice-cream in the cylinder= 10 × (volume of ice-cream in one cone)
i.e., 540π = 10 × 2πr3
⇒ r3 = \(\frac{540}{10 \times 2}\)
⇒ r3 = 27
⇒ r3 = 27 cm
⇒ r = 3 cm
Therefore, radius of ice cream cone is 3 cm.
OR
(B) A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of hemisphere is 12 cm and the total height of vessel is 10 cm. Find the inner surface area of the vessel.
Solution:
Here, vessel is a combination of a hollow hemi sphere and a hollow cylinder for cylindrical portion,
Diameter = AB = DC = 12 cm
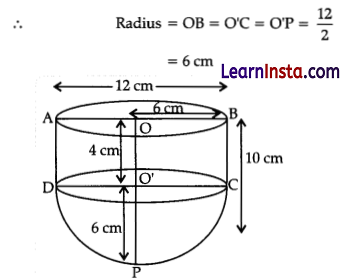
Total length of vessel, PO = 10 cm
∴ Length of cylinder, OO’ = PO – O’P
= 10 – 6 = 4 cm
For hemi spherical portion,
Radius of hemisphere = Height of hemisphere = 6 cm
Now, the inner surface area of vessel = Curved surface are of cylinder + curved surface area of hemisphere
= 2πrh + 2πr2
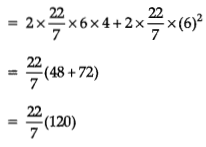
= 377.14
= 377 cm2
![]()
Question 35.
Find the unknown values in the following table:
| Class | Frequency (f) | Cumulative frequency |
| 0 – 10 | 5 | 5 |
| 10 – 20 | 7 | x1 |
| 20 – 30 | x2 | 18 |
| 30 – 40 | 5 | x3 |
| 40 – 50 | x4 | 30 |
Solution:
x1 = 5 + 7 = 12
x2 = 18 – x1 = 18 – 12 = 6
x3 = 18 + 5 = 23
and x4 = 30 – x3 = 30 – 23 = 7
Section – E (12 Marks)
Case study based questions are compulsory.
Question 36.
Read the passage below and answer the questions that follows:
Varun has been selected by his School to design logo for Sports Day T-shirts for students and staff. The logo is designed in different geometrical shapes and different colours according to the theme. In given figure, a circle with centre O is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. The lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively.
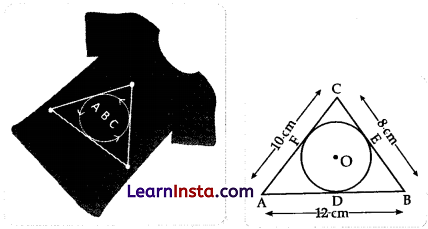
(i) Find the length of AD and BE.
OR
If the radius of the circle is 4 cm, find the area of ΔOAB.
Solution:
Let AD be x cm, then DB = (12 – x) cm
∵ AD = AF, CF = CE, DB = BE [Tangents to a circle from external points]
∴ AF = x cm,
then CF = (10 – x) cm
BE = (12 – x) cm,
then CE = 8 – (12 – x) = (x – 4) cm
Now CF = CE
10 – x = x – 4
2x = 14
⇒ x = 7. … (i)
Hence, AD = 7cm
Since, BE = (12 – x) cm
= (12 – 7) cm [From (i)]
= 5 cm
OR
Radius, OD = 4 cm
and AB = 12 cm
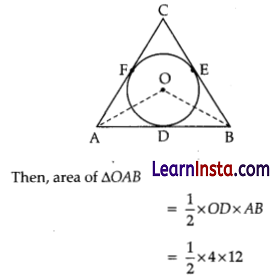
= 24 cm2
(ii) Find the perimeter of ΔABC.
Solution:
Perimeter of ΔABC = AB + BC + CA
= (12 + 8 + 10) cm
= 30 cm
(iii) Find the length of CE
Solution:
From question (i),
CF = (10 – x cm)
= (10 – 7) cm
= 3 cm
![]()
Question 37.
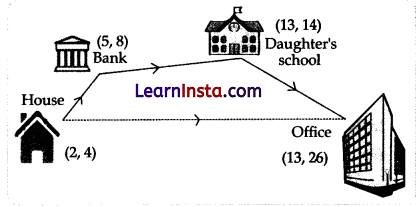
Read the following text and answer the following questions:
Aayush starts walking from his house to office. Instead of going to the office directly, he goes to a bank first, from there to his daughter’s school and then reaches the office.
(Assume that all distances covered are in straight lines). If the house is situated at (2, 4), bank at (5,8), school at (13, 14) and office at (13, 26) and co-ordinates are in km.
(i) What is the distance between house and bank?
OR
What is the distance between the bank and daughter’s school?
Solution:
Since,
Distance between two points (x1, y1) and (x2, y2).

(ii) What is the distance daughter’s school and office?
Solution:
Distance between daughter’s school and office,

(iii) What is the extra distance travelled by Aayush?
Solution:
Distance between two points (x1, y1) and (x2, y2).

= 24.59
= 24.6 km
Total distance = (House + Bank + School + Office travelled)
= (5 + 10 + 12) km
= 27 km
Extra distance travelled by Aayush in reaching his office = 27 – 24.6 = 2.4 km
Question 38.
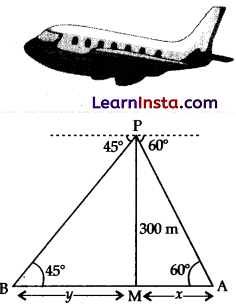
Read the following text and answer the questions that follow:
An aeroplane is a vehicle with wings and one or more engines that enable it to fly through the air. Most people think about inventors of aeroplane was Wrights brothers. We have discussed about an aeroplane as following:
An aeroplane at an altitude of 300 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°.
[Use √3 = 1.732]
(i) Find the value of y.
(ii) Find the value of x.
OR
Find the distance PB.
(iii) Find the width AB of the river.
Solution:

![]()
OR
In ΔPMB,
PM = 300 m,
BM = y = 300 m (proved in Q.(i)
and ΔPMB = 90°
∴ (PB)2 = (PM)2 + (BM)2 [Using Pythogoras Theorem]
= (300)2 + (300)2
= 90000 + 90000
= 180000
∴ PB = \(\sqrt{18 \times 10000}\)
= 100 x 3√2
= 300√2 m
(iii) We have proved that
x = 173.2 m and y = 300 m
∴ AB = x + y
= (173.2 + 300) m
= 473.2 m