ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test
Question 1.
Write the first four terms of the A.P. when its first term is – 5 and the common difference is – 3.
Solution:
First 4 term of A.P. whose first term (a) = -5
and common difference (d) = -3
= -5, -8, -11, -14
Question 2.
Verify that each of the following lists of numbers is an A.P., and the write its next three terms :
(i) \(0,\frac { 1 }{ 4 } ,\frac { 1 }{ 2 } ,\frac { 3 }{ 4 } ,… \)
(ii) \(5,\frac { 14 }{ 3 } ,\frac { 13 }{ 3 } ,4,… \)
Solution:
(i) \(0,\frac { 1 }{ 4 } ,\frac { 1 }{ 2 } ,\frac { 3 }{ 4 } ,… \)
Here a = 0, d = \(\\ \frac { 1 }{ 4 } \)
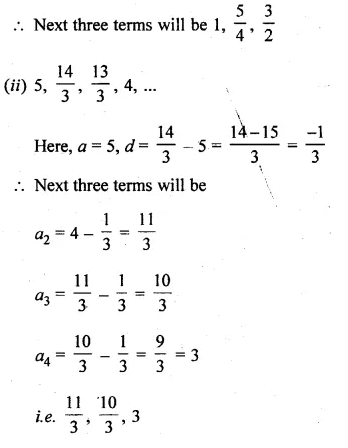
Question 3.
The nth term of an A.P. is 6n + 2. Find the common difference.
Solution:
Tn of an A.P. = 6n + 2 .
T1 = 6 x 1 + 2 = 6 + 2 = 8
T2 = 6 x 2 + 2 = 12 + 2 = 14
T3 = 6 x 3 + 2 = 18 + 2 = 20
d = 14 – 8 = 6
Question 4.
Show that the list of numbers 9, 12, 15, 18, … form an A.P. Find its 16th term and the nth.
Solution:
9, 12, 15, 18, …
Here, a = 9, d = 12 – 9 = 3
or 15 – 12 = 3
or 18 – 15 = 3
Yes, it form an A.P.
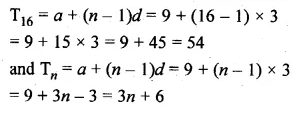
Question 5.
Find the 6th term from the end of the A.P. 17, 14, 11, …, – 40.
Solution:
6th term from the end of
A.P. = 17, 14, 11, …… 40
Here, a = 17, d = -3, l = -40
l = a + (n – 1 )d
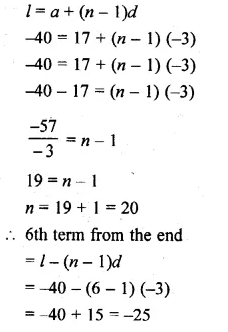
Question 6.
If the 8th term of an A.P. is 31 and the 15th term is 16 more than its 11th term, then find the A.P.
Solution:
In an A.P.
a8 = 31, a15 = a11 + 16
Let a be the first term and d be a common difference, then
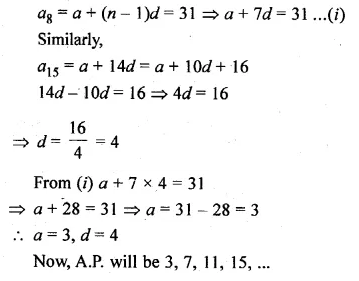
Question 7.
The 17th term of anA.P. is 5 more than twice its 8th term. If the 11th term of the A.P. is 43, then find the wth term.
Solution:
In an A.P.
a17 = 2 x a8 + 5
a11 = 43, find an
Let a be the first term and d be the common
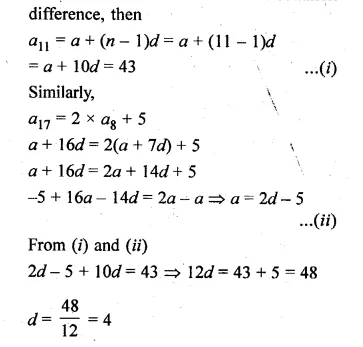
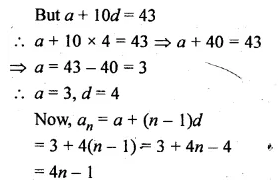
Question 8.
The 19th term of an A.P. is equal to three times its 6th term. If its 9th term is 19, find the A.P.
Solution:
In an A.P.
a19 = 3 x a6 and a9 = 19
Let a be the first term and d be the common
difference, then
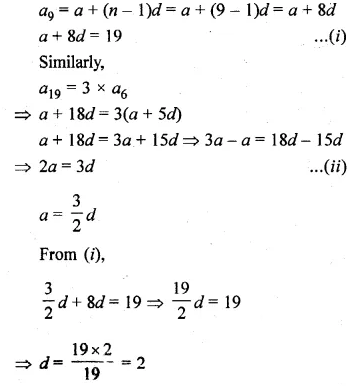
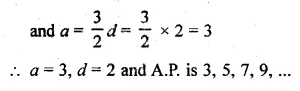
Question 9.
If the 3rd and the 9th terms of an A.P. are 4 and – 8 respectively, then which term of this A.P. is zero?
Solution:
In an A.P.
a3 = 4, a9 = -8, which term of A.P. will be zero
Let a be the first term and d be a common difference, then
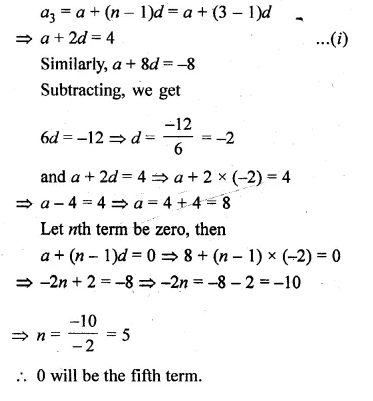
Question 10.
Which term of the list of numbers 5, 2, – 1, – 4, … is – 55?
Solution:
A.P. is 5, 2, -1, – 4, …
Which term of A.P. is -55
Let it be nth term
Here, a = 5, d = 2 – 5 = -3
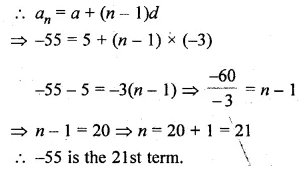
Question 11.
The 24th term of an A.P. is twice its 10th term. Show that its 72nd term is four times its 15th term.
Solution:
In an A.P.
24th term = 2 x 10th term
To show that 72nd term = 4 x 15th term
Let a be the first term and d be a common difference, then

Question 12.
Which term of the list of numbers \(20,19\frac { 1 }{ 4 } ,18\frac { 1 }{ 2 } ,17\frac { 3 }{ 4 } ,..\) is the first negative term?
Solution:
In A.P., which is the first negative term
\(20,19\frac { 1 }{ 4 } ,18\frac { 1 }{ 2 } ,17\frac { 3 }{ 4 } ,..\)
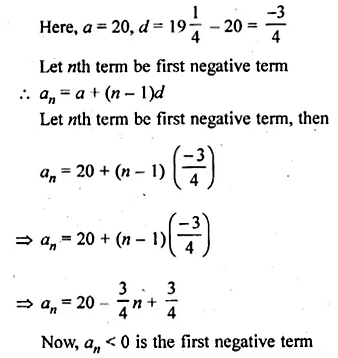
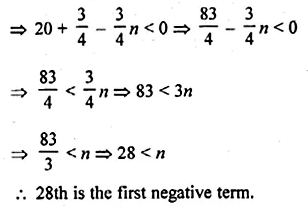
Question 13.
If the pth term of an A.P. is q and the qth term is p, show that its nth term is (p + q – n)
Solution:
In an A.P.
pth term = q
qth term = p
Show that (p + q – n) is nth term
Let a be the first term and d be the common

Question 14.
How many three digit numbers are divisible by 9?
Solution:
3-digit numbers which are divisible by 9 are 108, 117, 126, 135, …, 999
Here, a = 108, d = 9 and l = 999
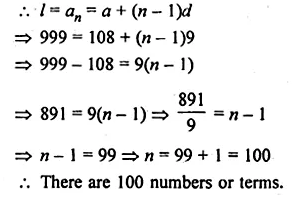
Question 15.
The sum of three numbers in A.P. is – 3 and the product is 8. Find the numbers.
Solution:
Sum of three numbers of an A.P. = -3
and their product = 8
Let the numbers be
a – d, a, a + d, then
a – d + a + a + d = -3
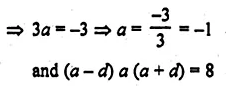
Question 16.
The angles of a quadrilateral are in A.P. If the greatest angle is double of the smallest angle, find all the four angles.
Solution:
Angles of a quadrilateral are in A.P.
Greatest angle is double of the smallest
Let the smallest angle of the quadrilateral is
a + 3d…..(i)

Question 17.
The nth term of an A.P. cannot be n² + n + 1. Justify your answer.
Solution:
nth term of an A.P. can’t be n² + n + 1
Giving some different values to n such as 1, 2, 3, 4, …
we find then

Question 18.
Find the sum of first 20 terms of an A.P. whose nth term is 15 – 4n.
Solution:
Giving some different values such as 1 to 20
We get,
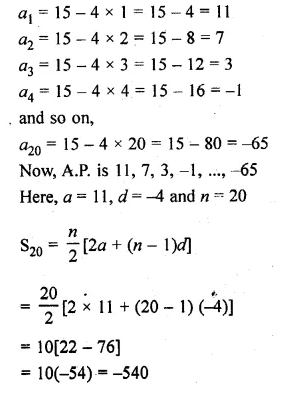
Question 19.
Find the sum :
\(18+15\frac { 1 }{ 2 } +13+…+\left( -49\frac { 1 }{ 2 } \right) \)
Solution:
Find the sum
\(18+15\frac { 1 }{ 2 } +13+…+\left( -49\frac { 1 }{ 2 } \right) \)
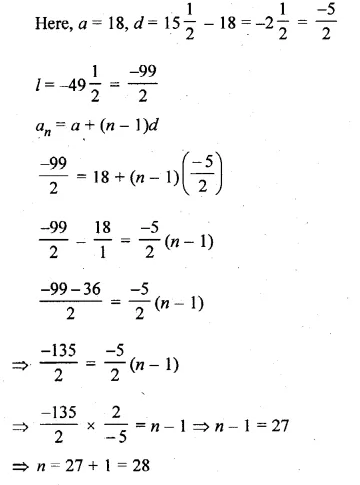
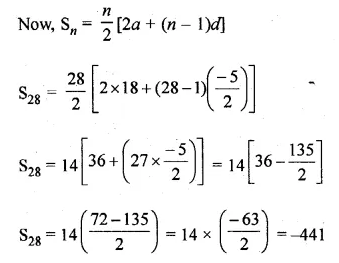
Question 20.
(i) How many terms of the A.P. – 6,\(– \frac { 11 }{ 2 } \) – 5,… make the sum – 25?
(ii) Solve the equation 2 + 5 + 8 + … + x = 155.
Solution:
(i) Sum = -25
A.P. = -6, \(– \frac { 11 }{ 2 } \) -5,…
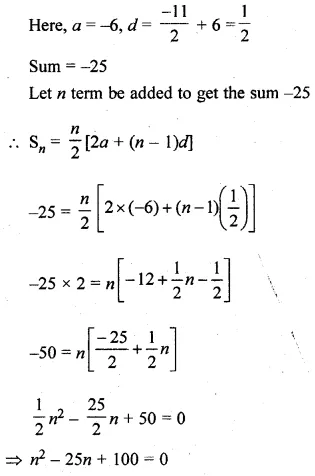
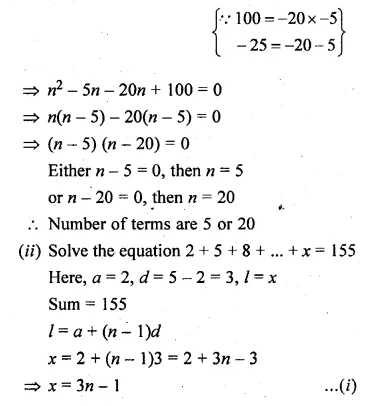
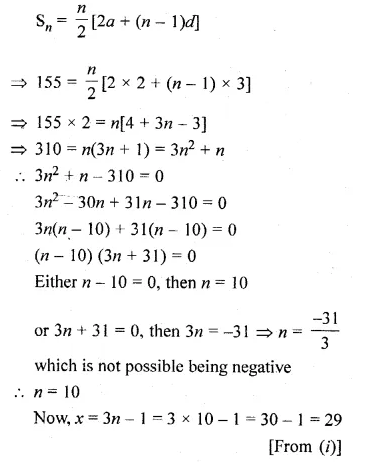
Question 21.
If the third term of an A.P. is 5 and the ratio of its 6th term to the 10th term is 7 : 13, then find the sum of first 20 terms of this A.P.
Solution:
3rd term of an A.P. = 5
Ratio in 6th term and 10th term = 7 : 13
Find S20
Let a be the first term and d be the common difference
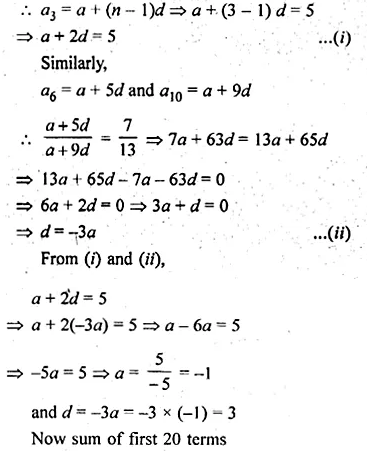
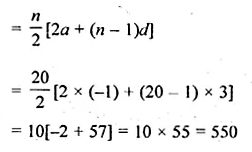
Question 22.
In an A.P., the first term is 2 and the last term is 29. If the sum of the terms is 155, then find the common difference of the A.P.
Solution:
In an A.P.
First term (a) = 2
Last term (l) = 29
Sum of terms = 155
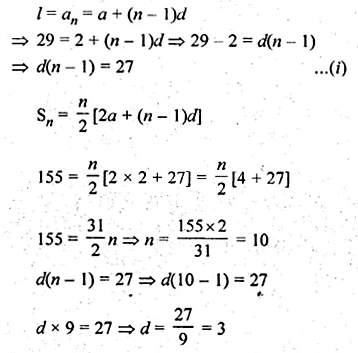
Question 23.
The sum of first 14 terms of an A.P. is 1505 and its first term is 10. Find its 25th term.
Solution:
Sum of first 14 terms = 1505
First term (a) = 10
Find 25th term
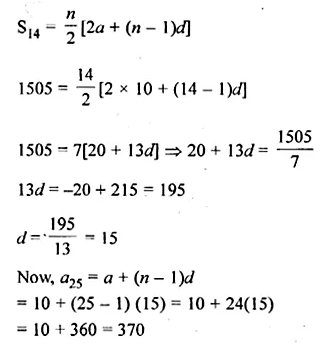
Question 24.
Find the number of terms of the A.P. – 12, – 9, – 6, …, 21. If 1 is added to each term of this A.P., then find the sum of all terms of the A.P. thus obtained.
Solution:
A.P. -12, -9, -6,…, 21
If 1 is added to each term, find the sum of there terms
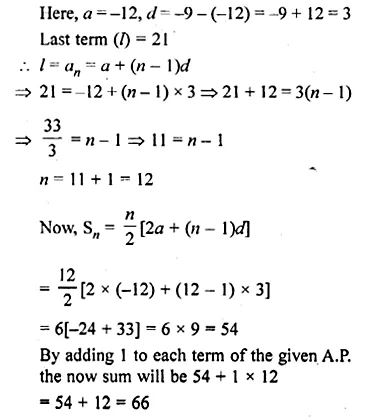
Question 25.
The sum of first n term of an A.P. is 3n² + 4n. Find the 25th term of this A.P.
Solution:
Sn = 3n² + 4n
Sn – 1 = 3(n – 1)² + 4(n – 1)
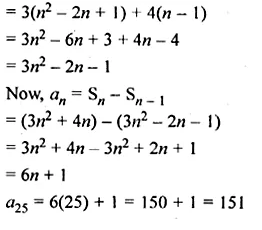
Question 26.
In an A.P., the sum of first 10 terms is – 150 and the sum of next 10 terms is – 550. Find the A.P.
Solution:
In an A.P.
Sum of first 10 terms = -150
Sum of next 10 terms = -550, A.P. = ?
Sum of first 10 terms = -150
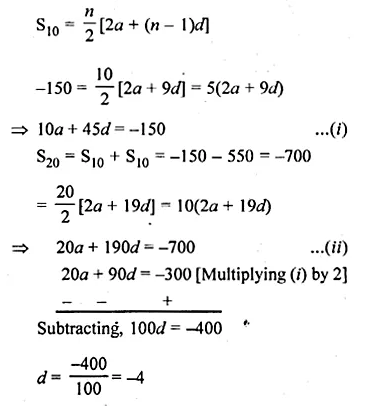
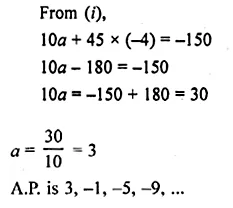
Question 27.
The sum of first m terms of an A.P. is 4m² – m. If its nth term is 107, find the value of n. Also find the 21 st term of this A.P.
Solution:
Sm = 4m² – m
Sn = 4n² – n
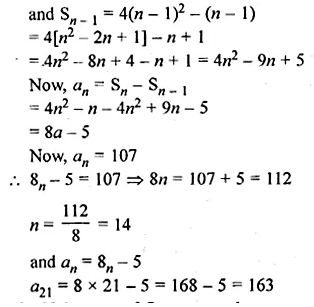
Question 28.
If the sum of first p, q and r terms of an A.P. are a, b and c respectively, prove that
\(\frac { a }{ p } (q-r)+\frac { b }{ q } (r-p)+\frac { c }{ r } (p-q)=0 \)
Solution:
Let the first term of A.P. be A and common difference be d.
Sum of the first p terms is
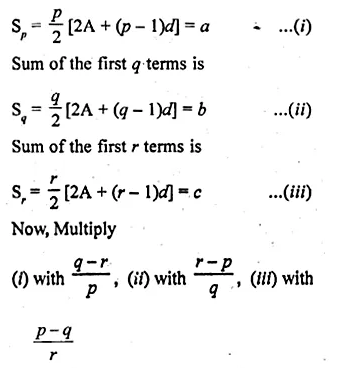
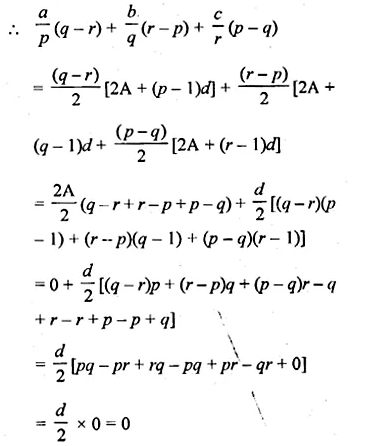
![]()
Question 29.
A sum of Rs 700 is to be used to give 7 cash prizes to students of a school for their overall academic performance. If each prize is Rs 20 less than its preceding prize, find the value of each of the prizes.
What is the importance of an academic prise in students life? (Value Based)
Solution:
Total sum = Rs 700
Cash prizes to 7 students = 7 prize
Each prize is Rs 20 less than its preceding prize
d = -20, d = -20, n = 7
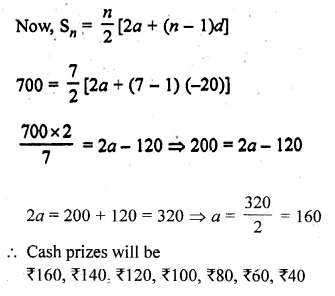
Question 30.
Find the geometric progression whose 4th term is 54 and 7th term is 1458.
Solution:
In a G.P.
a4 = 54
a7 = 1458
Let a be the first term and r be the common difference
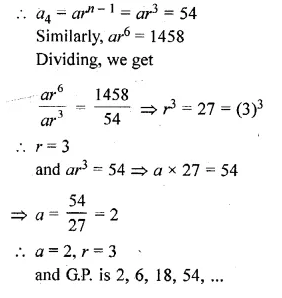
Question 31.
The fourth term of a G.P. is the square of its second term and the first term is – 3. Find its 7th term.
Solution:
In G.P.
a4 = (a2)², a1 = -3
Let a be the first term and r be the common ratio
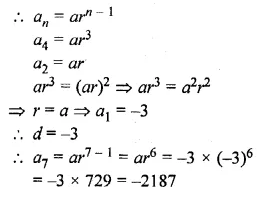
Question 32.
If the 4th, 10th and 16th terms of a G.P. are x, y and z respectively, prove that x, y and z are in G.P.
Solution:
In a G.P.
a4 = x, a10 = y, a16 = z
Show that x, y, z are in G.P.
Let a be the first term and r be the common ratio, then
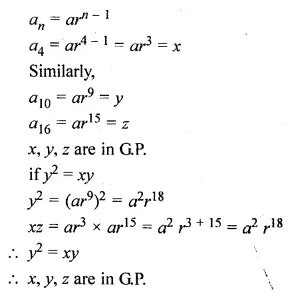
Question 33.
The original cost of a machine is Rs 10000. If the annual depreciation is 10%, after how many years will it be valued at Rs 6561 ?
Solution:
Original cost of machine = Rs 10000
Since, machine depreciates at the rate of 10%
on reducing the balance,
Value of machine after one year

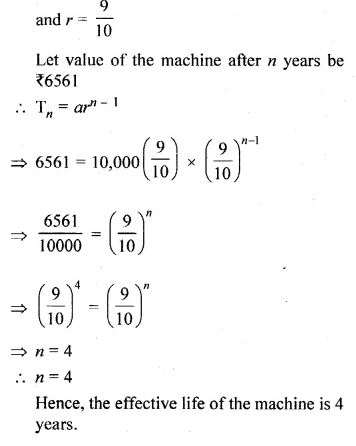
Question 34.
How many terms of the G.P. \(3,\frac { 3 }{ 2 } ,\frac { 3 }{ 4 } \),are needed to give the sum \(\\ \frac { 3069 }{ 512 } \) ?
Solution:
G.P. \(3,\frac { 3 }{ 2 } ,\frac { 3 }{ 4 } \)
Sn = \(\\ \frac { 3069 }{ 512 } \)
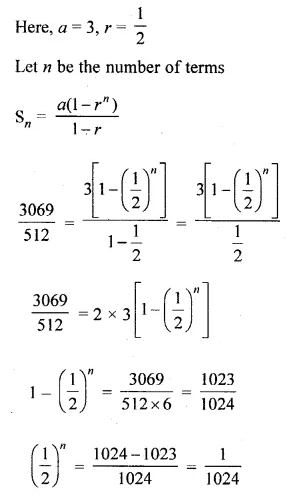
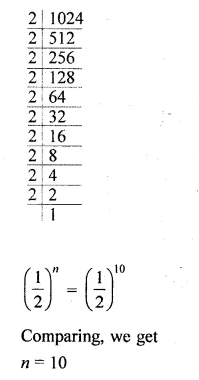
Question 35.
Find the sum of first n terms of the series : 3 + 33 + 333 + …
Solution:
Series is
3 + 33 + 333 + … n terms
= 3[1 + 11 + 111 +…n terms]
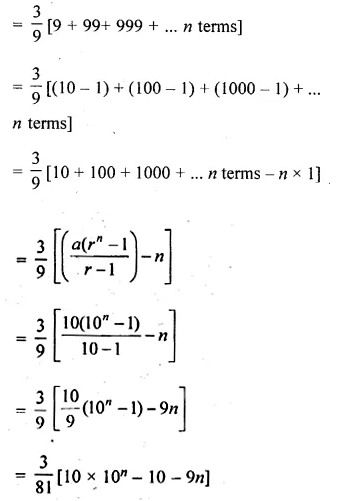
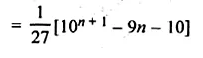
Question 36.
Find the sum of the series 7 + 7.7 + 7.77 + 7.777 + … to 50 terms.
Solution:
The given sequence is 7, 7.7, 7.77, 7.777,…
Required sum = S50
= 7 + 7.7 + 7.77 + … 50 terms
= 7(1 + 1.1 + 1. 11 + … 50 terms)

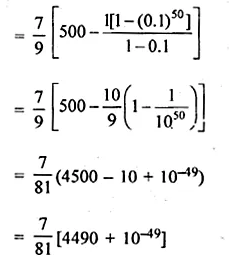
Question 37.
The inventor of chessboard was a very clever man. He asked the king, h reward of one grain of wheat for the first square, 2 grains for the second, 4 grains for the third, and so on, doubling the number of the grains for each subsequent square. How many grains would have to be given?
Solution:
In a chessboard, there are 8 x 8 = 64 squares
If a man put 1 grain in first square,
2 grains in second square,
4 grains in third square
and goes on upto the last square, i.e. 64th square
Therefore, 1 + 2 + 4 + 8 + 16 + … 64 terms
Here, a = 1, r = 2 and n = 64
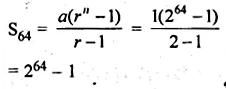
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.