ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Ex 6
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Ex 6
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization EX 6
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Chapter Test
Question 1.
Find the remainder (without divisions) on dividing f(x) by x – 2, where
(i) f(x) = 5x2 – 1x + 4
(ii) f (x) = 2x3 – 7x2 + 3
Solution:
Let x – 2 = 0, then x = 2
(i) Substituting value of x in f(x)
f(x) = 5x2 – 7x + 4
⇒ f(2) = 5(2)2 – 7(2) + 4
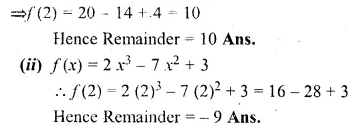
Question 2.
Using remainder theorem, find the remainder on dividing f(x) by (x + 3) where
(i) f(x) = 2x2 – 5x + 1
(ii) f(x) = 3x3 + 7x2 – 5x + 1
Solution:
Let x + 3 = 0
⇒ x = -3
Substituting the value of x in f(x),
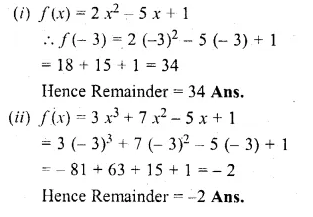
Question 3.
Find the remainder (without division) on dividing f(x) by (2x + 1) where
(i) f(x) = 4x2 + 5x + 3
(ii) f(x) = 3x3 – 7x2 + 4x + 11
Solution:
Let 2x + 1 = 0, then x = \(– \frac { 1 }{ 2 } \)
Substituting the value of x in f(x):
(i) f(x) = 4x2 + 5x + 3
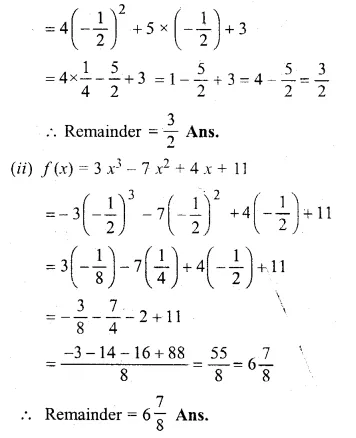
Question 4.
(i) Find the remainder (without division) when 2x3 – 3x2 + 7x – 8 is divided by x – 1 (2000)
(ii) Find the remainder (without division) on dividing 3x2 + 5x – 9 by (3x + 2)
Solution:
(i) Let x – 1 = 0, then x = 1
Substituting value of x in f(x)
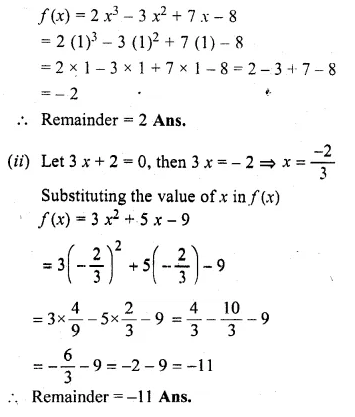
Question 5.
Using remainder theorem, find the value of k if on dividing 2x3 + 3x2 – kx + 5 by x – 2, leaves a remainder 7. (2016)
Solution:
f(x) = 2x2 + 3x2 – kx + 5
g(x) = x – 2, if x – 2 = 0, then x = 2
Dividing f(x) by g(x) the remainder will be
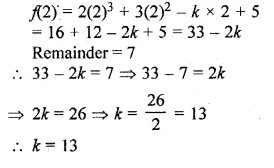
Question 6.
Using remainder theorem, find the value of a if the division of x3 + 5x2 – ax + 6 by (x – 1) leaves the remainder 2a.
Solution:
Let x – 1 = 0, then x = 1
Substituting the value of x in f(x)
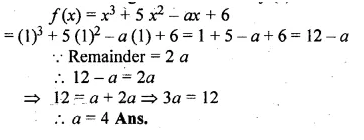
Question 7.
(i) What number must be subtracted from 2x2 – 5x so that the resulting polynomial leaves the remainder 2, when divided by 2x + 1 ?
(ii) What number must be added to 2x3 – 7x2 + 2x so that the resulting polynomial leaves the remainder – 2 when divided by 2x – 3?
Solution:
(i) Let a be subtracted from 2x2 – 5x,
Dividing 2x2 – 5x by 2x + 1,
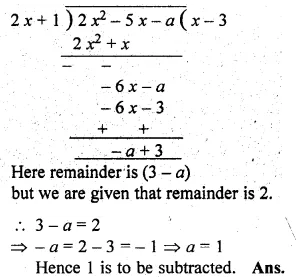
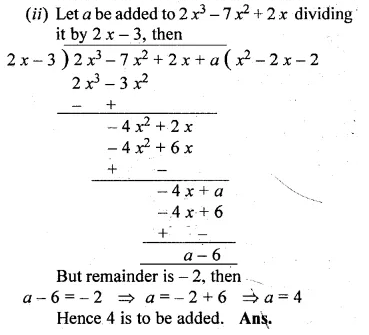
Question 8.
(i) When divided by x – 3 the polynomials x2 – px2 + x + 6 and 2x3 – x2 – (p + 3) x – 6 leave the same remainder. Find the value of ‘p’
(ii) Find ‘a’ if the two polynomials ax3 + 3x2 – 9 and 2x3 + 4x + a, leaves the same remainder when divided by x + 3.
Solution:
By dividing
x3 – px2 + x + 6
and 2x3 – x2 – (p + 3) x – 6
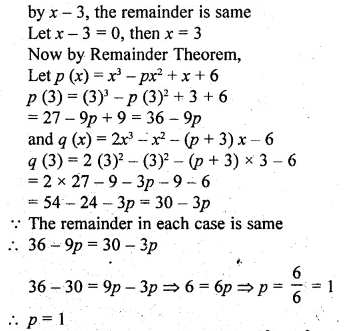
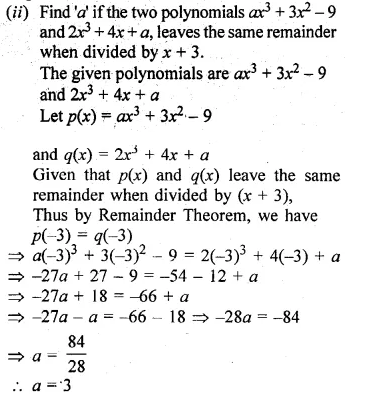
Question 9.
By factor theorem, show that (x + 3) and (2x – 1) are factors of 2x2 + 5x – 3.
Solution:
Let x + 3 = 0 then x = – 3
Substituting the value of x in f(x)
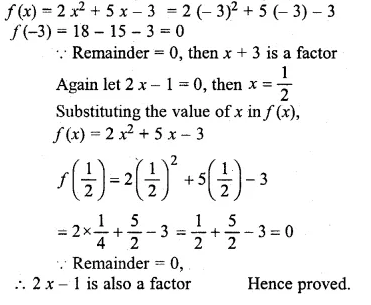
Question 10.
Show that (x – 2) is a factor of 3x2 – x – 10 Hence factorise 3x2 – x – 10.
Solution:
Let x – 2 = 0, then x = 2
Substituting the value of x in f(x),
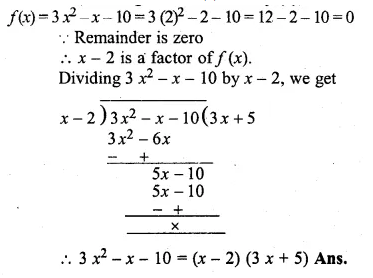
Question 11.
Show that (x – 1) is a factor of x3 – 5x2 – x + 5 Hence factorise x3 – 5x2 – x + 5.
Solution:
Let x – 1 = 0, then x = 1
Substituting the value of x in f(x),
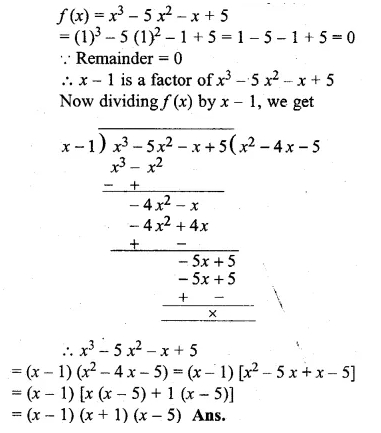
Question 12.
Show that (x – 3) is a factor of x3 – 7x2 + 15x – 9. Hence factorise x3 – 7x2 + 15 x – 9
Solution:
Let x – 3 = 0, then x = 3,
Substituting the value of x in f(x),
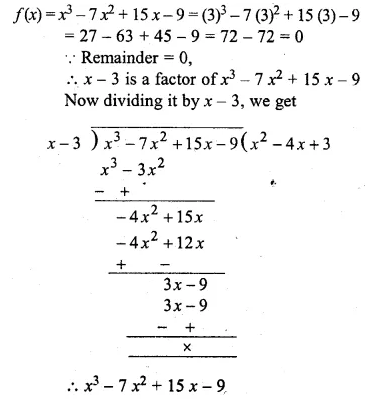
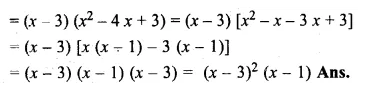
Question 13.
Show that (2x + 1) is a factor of 4x3 + 12x2 + 11 x + 3 .Hence factorise 4x3 + 12x2 + 11x + 3.
Solution:
Let 2x + 1 = 0,
then x = \(– \frac { 1 }{ 2 } \)
Substituting the value of x in f(x),
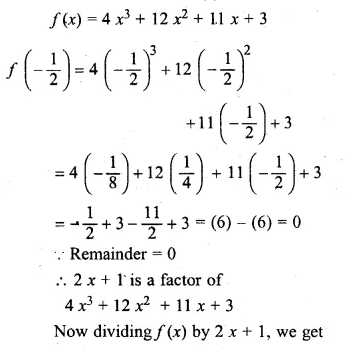
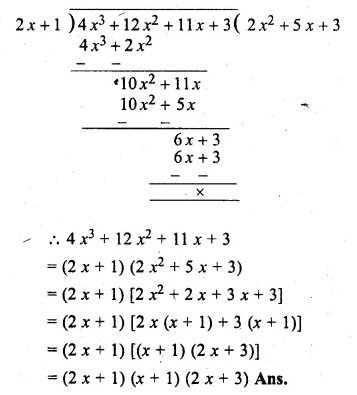
Question 14.
Show that 2x + 7 is a factor of 2x3 + 5x2 – 11x – 14. Hence factorise the given expression completely, using the factor theorem. (2006)
Solution:
Let 2x + 7 = 0, then 2x = -7
x = \(\\ \frac { -7 }{ 2 } \)
substituting the value of x in f(x),
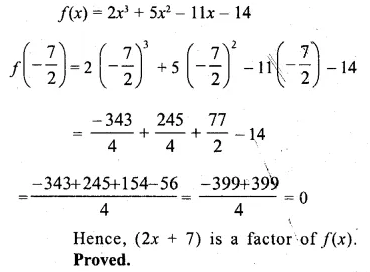
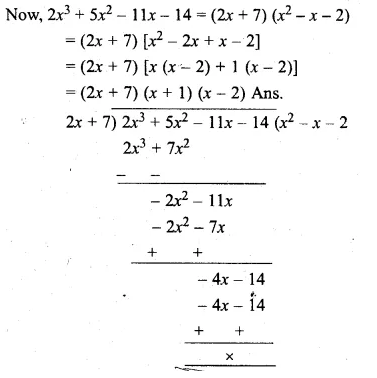
Question 15.
Use factor theorem to factorise the following polynominals completely.
(i) x3 + 2x2 – 5x – 6
(ii) x3 – 13x – 12.
Solution:
(i) Let f(x) = x3 + 2x2 – 5x – 6
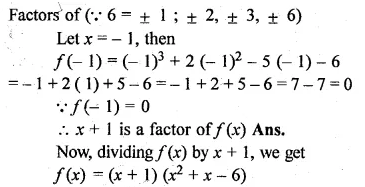
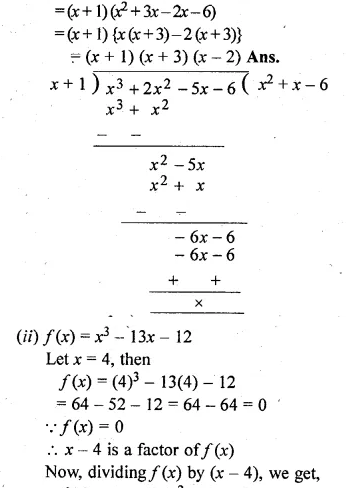
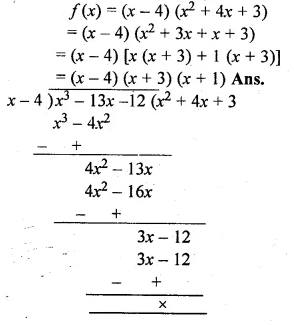
Question 16.
(i) Use the Remainder Theorem to factorise the following expression : 2x3 + x2 – 13x + 6. (2010)
(ii) Using the Remainder Theorem, factorise completely the following polynomial: 3x2 + 2x2 – 19x + 6 (2012)
Solution:
(i) Let f(x) = 2x3 + x2 – 13x + 6
Factors of 6 are ±1, ±2, ±3, ±6
Let x = 2, then
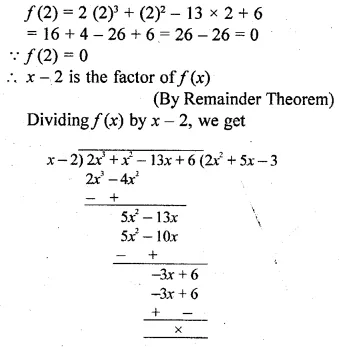
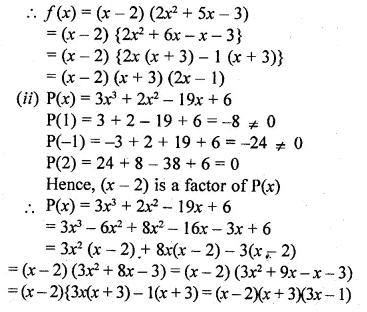
Question 17.
Using the Remainder and Factor Theorem, factorise the following polynomial: x3 + 10x2 – 37x + 26.
Solution:
f(x) = x3 + 10x2 – 37x + 26
f(1) = (1)3 + 10(1)2 – 37(1) + 26
= 1 + 10 – 37 + 26 = 0
x = 1
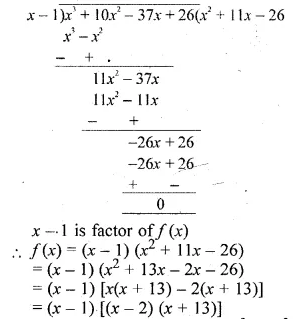
Question 18.
If (2 x + 1) is a factor of 6x3 + 5x2 + ax – 2 find the value of a
Solution:
Let 2x + 1 = 0, then x = \(– \frac { 1 }{ 2 } \)
Substituting the value of x in f(x),
f(x) = 6x3 + 5x2 + ax – 2
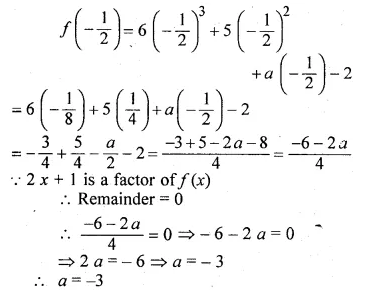
Question 19.
If (3x – 2) is a factor of 3x3 – kx2 + 21x – 10, find the value of k.
Solution:
Let 3x – 2 = 0, then 3x = 2
⇒ x = \(\\ \frac { 2 }{ 3 } \)
Substituting the value of x in f(x),
f(x) = 3x3 – kx2 + 21x – 10
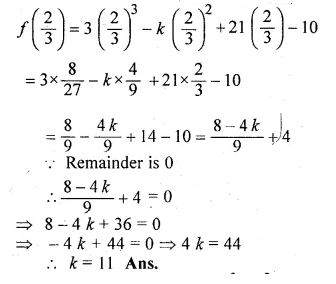
Question 20.
If (x – 2) is a factor of 2x3 – x2 + px – 2, then
(i) find the value of p.
(ii) with this value of p, factorise the above expression completely
Solution:
(i) Let x – 2 = 0, then x = 2
Now f(x) = 2x3 – x2 + px – 2
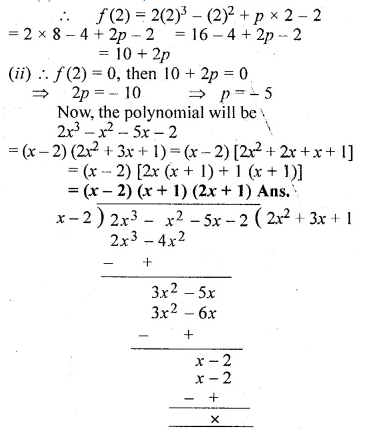
Question 21.
Find the value of ‘K’ for which x = 3 is a solution of the quadratic equation, (K + 2)x2 – Kx + 6 = 0.
Also, find the other root of the equation.
Solution:
(K + 2)x2 – Kx + 6 = 0 …(1)
Substitute x = 3 in equation (1)
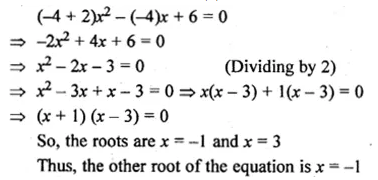
Question 22.
What number should be subtracted from 2x3 – 5x2 + 5x so that the resulting polynomial has 2x – 3 as a factor?
Solution:
Let the number to be subtracted be k and the resulting polynomial be f(x), then
f(x) = 2x3 – 5x2 + 5x – k
Since, 2x – 3 is a factor of f(x),
Now, converting 2x – 3 to factor theorem
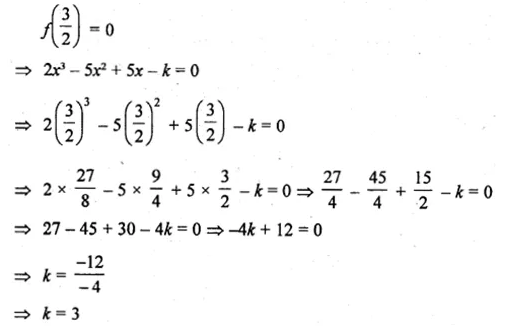
Question 23.
Find the value of the constants a and b, if (x – 2) and (x + 3) are both factors of the expression x3 + ax2 + bx – 12.
Solution:
Let x – 2 = 0, then x = 0
Substituting value of x in f(x)
f(x) = x3 + ax2 + bx – 12
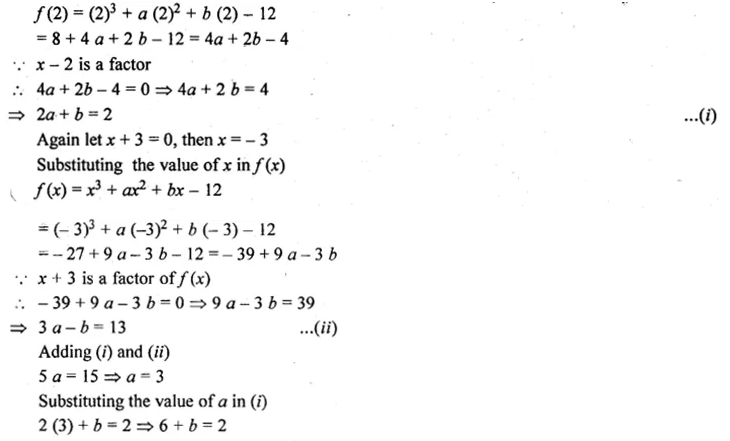
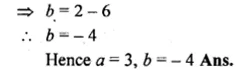
Question 24.
If (x + 2) and (x – 3) are factors of x3 + ax + b, find the values of a and b. With these values of a and b, factorise the given expression.
Solution:
Let x + 2 = 0, then x = -2
Substituting the value of x in f(x),
f(x) = x3 + ax + b


Question 25.
(x – 2) is a factor of the expression x3 + ax2 + bx + 6. When this expression is divided by (x – 3), it leaves the remainder 3. Find the values of a and b. (2005)
Solution:
As x – 2 is a factor of
f(x) = x3 + ax2 + bx + 6

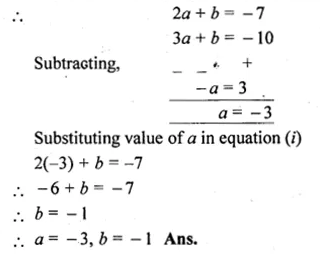
Question 26.
If (x – 2) is a factor of the expression 2x3 + ax2 + bx – 14 and when the expression is divided by (x – 3), it leaves a remainder 52, find the values of a and b.
Solution:
f(x) = 2x3 + ax2 + bx – 14
∴ (x – 2) is factor of f(x)
f(2) = 0
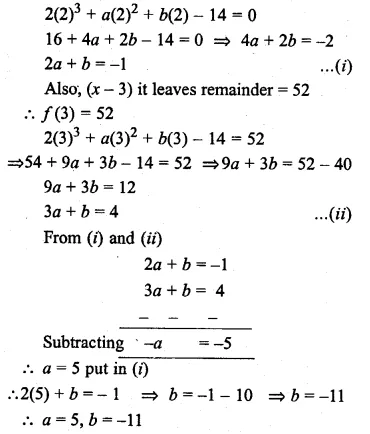
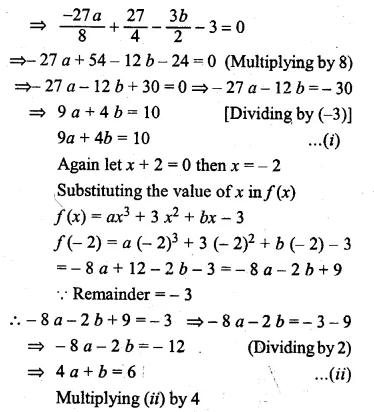
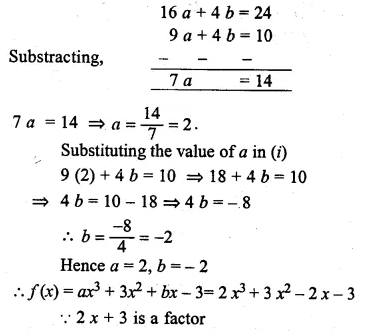
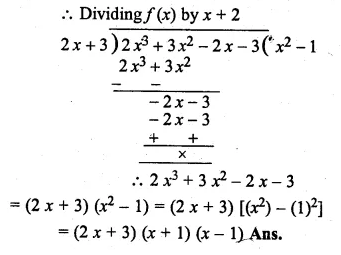
Question 27.
If ax3 + 3x2 + bx – 3 has a factor (2x + 3) and leaves remainder – 3 when divided by (x + 2), find the values of a and 6. With these values of a and 6, factorise the given expression.
Solution:
Let 2x + 3 = 0 then 2x = -3
⇒ x = \(\\ \frac { -3 }{ 2 } \)
Substituting the value of x in f(x),
f(x) = ax3 + 3x2 + 6x – 3
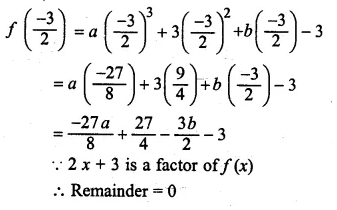
Question 28.
Given f(x) = ax2 + bx + 2 and g(x) = bx2 + ax + 1. If x – 2 is a factor of f(x) but leaves the remainder – 15 when it divides g(x), find the values of a and b. With these values of a and b, factorise the expression. f(x) + g(x) + 4x2 + 7x.
Solution:
f(x) = ax2 + bx + 2
g(x) = bx2 + ax + 1
x – 2 is a factor of f(x)
Let x – 2 = 0
⇒ x = 2
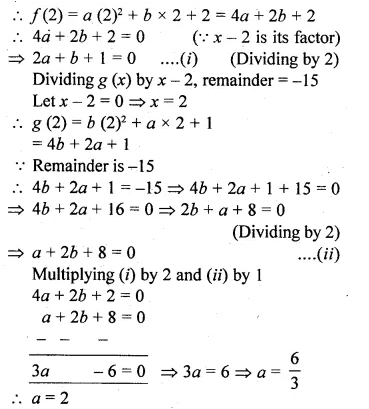
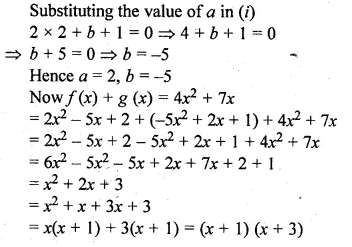
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Ex 6 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.