ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test
Question 1.
A game consists of spinning an arrow which comes to rest at one of the regions 1, 2 or 3 (shown in the given figure). Are the outcomes 1, 2 and 3 equally likely to occur? Give reasons.
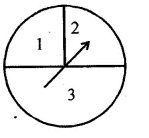
Solution:
In a game,
No, the outcomes are not equally likely.
Outcome 3 is more likely to occur than the outcomes of 1 and 2.
Question 2.
In a single throw of a die, find the probability of getting
(i) a number greater than 5
(ii) an odd prime number
(iii) a number which is multiple of 3 or 4.
Solution:
In a single throw of a die
Number of total outcomes = 6 (1, 2, 3, 4, 5, 6)
(i) Numbers greater than 5 = 6 i.e., one number
Probability = \(\\ \frac { 1 }{ 6 } \)
(ii) An odd prime number 2 i.e., one number
Probability = \(\\ \frac { 1 }{ 6 } \)
(iii) A number which is a multiple of 3 or 4 which are 3, 6, 4 = 3 numbers
Probability = \(\\ \frac { 3 }{ 6 } \) = \(\\ \frac { 1 }{ 2 } \)
Question 3.
A lot consists of 144 ball pens of which 20 are defective and the others are good. Rohana will buy a pen if it is good, but will not buy it if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that :
(i) She will buy it?
(ii) She will not buy it?
Solution:
In a lot, there are 144 ball pens in which defective ball pens are = 20
and good ball pens are = 144 – 20 = 124
Rohana buys a pen which is good only.
(i) Now the number of possible outcomes = 144
and the number of favourable outcomes = 124

Question 4.
A lot consists of 48 mobile phones of which 42 are good, 3 have only minor defects and 3 have major defects. Varnika will buy a phone if it is good but the trader will only buy a mobile if it has no major defect. One phone is selected at random from the lot. What is the probability that it is
(i) acceptable to Varnika?
(ii) acceptable to the trader?
Solution:
Number of total mobiles = 48
Number of good mobiles = 42
Number having minor defect = 3
Number having major defect = 3
(i) Acceptable to Varnika = 42
Probability = \(\\ \frac { 42 }{ 48 } \) = \(\\ \frac { 7 }{ 8 } \)
(ii) Acceptable to trader = 42 + 3 = 45
Probability = \(\\ \frac { 45 }{ 48 } \) = \(\\ \frac { 15 }{ 16 } \)
Question 5.
A bag contains 6 red, 5 black and 4 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is
(i) white
(ii) red
(iii) not black
(iv) red or white.
Solution:
Total number of balls = 6 + 5 + 4 = 15
Number of red balls = 6
Number of black balls = 5
Number of white balls = 4
(i) Probability of a white ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 4 }{ 15 } \)
(ii) Probability of red ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 6 }{ 15 } \) = \(\\ \frac { 2 }{ 5 } \)
(iii) Probability of not black ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 15-5 }{ 15 } \)
= \(\\ \frac { 10 }{ 15 } \)
= \(\\ \frac { 2 }{ 3 } \)
(iv) Probability of red or white ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6+4 }{ 15 } \)
= \(\\ \frac { 10 }{ 15 } \)
= \(\\ \frac { 2 }{ 3 } \)
Question 6.
A bag contains 5 red, 8 white and 7 black balls. A ball is drawn from the bag at random. Find the probability that the drawn ball is:
(i) red or white
(ii) not black
(iii) neither white nor black
Solution:
Total number of balls in a bag = 5 + 8 + 7 = 20
(i) Number of red or white balls = 5 + 8 = 13
Probability of red or white ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 13 }{ 20 } \)
(ii) Number of ball which are not black = 20 – 7 = 13
Probability of not black ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 13 }{ 20 } \)
(iii) Number of ball which are neither white nor black
= Number of ball which are only red = 5
Probability of neither white nor black ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5 }{ 20 } \)
= \(\\ \frac { 1 }{ 4 } \)
Question 7.
A bag contains 5 white balls, 7 red balls, 4 black balls and 2 blue balls. One ball is drawn at random from the bag. What is the probability that the ball drawn is :
(i) white or blue
(ii) red or black
(iii) not white
(iv) neither white nor black ?
Solution:
Number of total balls = 5 + 7 + 4 + 2 = 18
Number of white balls = 5
number of red balls = 7
number of black balls = 4
and number of blue balls = 2.
(i) Number of white and blue balls = 5 + 2 = 7
Probability of white or blue balls will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 7 }{ 18 } \)
(ii) Number of red and black balls = 7 + 4 = 11
Probability of red or black balls will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 11 }{ 18 } \)
(iii) Number of ball which are not white = 7 + 4 + 2 = 13
Probability of not white balls will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 13 }{ 18 } \)
(iv) Number of balls which are neither white nor black = 18 – (5 + 4) = 18 – 9 = 9
Probability of ball which is neither white nor black will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 9 }{ 18 } \) = \(\\ \frac { 1 }{ 2 } \)
Question 8.
A box contains 20 balls bearing numbers 1, 2, 3, 4,……, 20. A ball is drawn at random from the box. What is the probability that the number on the ball is
(i) an odd number
(ii) divisible by 2 or 3
(iii) prime number
(iv) not divisible by 10?
Solution:
In a box, there are 20 balls containing 1 to 20 number
Number of possible outcomes = 20
(i) Numbers which are odd will be,
1, 3, 5, 7, 9, 11, 13, 15, 17, 19 = 10 balls.
Probability of odd ball will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 10 }{ 20 } \) = \(\\ \frac { 1 }{ 2 } \)
(ii) Numbers which are divisible by 2 or 3 will be
2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20 = 13 balls
Probability of ball which is divisible by 2 or 3 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 13 }{ 20 } \)
(iii) Prime numbers will be 2, 3, 5, 7, 11, 13, 17, 19 = 8
Probability of prime number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 8 }{ 20 } \) = \(\\ \frac { 2 }{ 5 } \)
(iv) Numbers not divisible by 10 will be
1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19 = 18
Probability of prime number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 18 }{ 20 } \) = \(\\ \frac { 9 }{ 10 } \)
Question 9.
Find the probability that a number selected at random from the numbers 1, 2, 3,……35 is a
(i) prime number
(ii) multiple of 7
(iii) multiple of 3 or 5.
Solution:
Numbers are 1, 2, 3, 4, 5,…..30, 31, 32, 33, 34, 35
Total = 35
(i) Prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31
which are 11
Probability of prime number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 11 }{ 35 } \)
(ii) Multiple of 7 are 7, 14, 21, 28, 35 which are 5
Probability of multiple of 7 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 5 }{ 35 } \) = \(\\ \frac { 1 }{ 7 } \)
(iii) Multiple of 3 or 5 are 3, 5, 6, 9, 10, 12 ,15, 18, 20, 21, 24, 25, 27, 30, 33, 35.
Which are 16 in numbers
Probability of multiple of 3 or 5 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 16 }{ 35 } \)
Question 10.
Cards marked with numbers 13, 14, 15,…..60 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that the number on the card is
(i) divisible by 5
(ii) a number which is a perfect square.
Solution:
Number of cards which are marked with numbers
13, 14, 15, 16, 17,….to 59, 60 are = 48
(i) Numbers which are divisible by 5 will be
15, 20, 25, 30, 35, 40, 45, 50, 55, 60 = 10
Probability of number divisible by 5 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 10 }{ 48 } \) = \(\\ \frac { 5 }{ 24 } \)
(ii) Numbers which is a perfect square are 16, 25, 36, 49 which are 4 in numbers.
Probability of number which is a perfect square will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 4 }{ 48 } \) = \(\\ \frac { 1 }{ 12 } \)
Question 11.
The box has cards numbered 14 to 99. Cards are mixed thoroughly and a card is drawn at random from the box. Find the probability that the card drawn from the box has
(i) an odd number
(ii) a perfect square number.
Solution:
Cards in a box are from 14 to 99 = 86
No. of total cards = 86
One card is drawn at random
Cards bearing odd numbers are 15, 17, 19, 21, …, 97, 99
Which are 43
(i) P(E) = \(\frac { Number\quad of\quad actual\quad events }{ Number\quad of\quad total\quad events } \)
= \(\\ \frac { 43 }{ 86 } \)
= \(\\ \frac { 1 }{ 2 } \)
(ii) Cards bearing number which are a perfect square
= 16, 25, 36, 49, 64, 81
Which are 6
P(E) = \(\frac { Number\quad of\quad actual\quad events }{ Number\quad of\quad total\quad events } \)
= \(\\ \frac { 6 }{ 86 } \)
= \(\\ \frac { 3 }{ 43 } \)
Question 12.
A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is four times that of a red ball, find the number of balls in the bags.
Solution:
Number of red balls = 5
and let number of blue balls = x
Total balls in the bag = 5 + x
and that of red balls = \(\\ \frac { 5 }{ 5+x } \)
According to the condition,
\(\frac { x }{ 5+x } =4\times \frac { 5 }{ 5+x } =>\frac { x }{ 5+x } =\frac { 20 }{ 5+x } \)
x ≠ – 5
x = 20
Hence, number of blue balls = 20
and number of balls in the bag = 20 + 5 = 25
Question 13.
A bag contains 18 balls out of which x balls are white.
(i) If one ball is drawn at random from the bag, what is the probability that it is white ball?
(ii) If 2 more white balls are put in the bag, the probability of drawing a white ball will be \(\\ \frac { 9 }{ 8 } \) times that of probability of white ball coming in part (i). Find the value of x.
Solution:
Total numbers of balls in a bag = 18
No. of white balls = x
(i) One ball is drawn a random
Probability of being a white ball = \(\\ \frac { x }{ 18 } \)
(ii) If 2 more white balls an put, then number of white balls = x + 2
and probability is \(\\ \frac { 9 }{ 8 } \) times
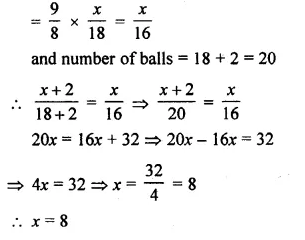
Question 14.
A card is drawn from a well-shuffled pack of 52 cards. Find the probability that the card drawn is :
(i) a red face card
(ii) neither a club nor a spade
(iii) neither an ace nor a king of red colour
(iv) neither a red card nor a queen
(v) neither a red card nor a black king.
Solution:
Number of cards in a pack of well-shuffled cards = 52
(i) Number of a red face card = 3 + 3 = 6
Probability of red face card will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 6 }{ 52 } \) = \(\\ \frac { 3 }{ 26 } \)
(ii) Number of cards which is neither a club nor a spade = 52 – 26 = 26
Probability of card which’ is neither a club nor a spade will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 26 }{ 52 } \) = \(\\ \frac { 1 }{ 2 } \)
(iii) Number of cards which is neither an ace nor a king of red colour
= 52 – (4 + 2) = 52 – 6 = 46
Probability of card which is neither ace nor a king of red colour will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 46 }{ 52 } \) = \(\\ \frac { 23 }{ 26 } \)
(iv) Number of cards which are neither a red card nor a queen are
= 52 – (26 + 2) = 52 – 28 = 24
Probability of card which is neither red nor a queen will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 24 }{ 52 } \) = \(\\ \frac { 6 }{ 13 } \)
(v) Number of cards which are neither red card nor a black king
= 52 – (26 + 2) = 52 – 28 = 24
Probability of cards which is neither red nor a black king will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 24 }{ 52 } \) = \(\\ \frac { 6 }{ 13 } \)
Question 15.
From pack of 52 playing cards, blackjacks, black kings and black aces are removed and then the remaining pack is well-shuffled. A card is drawn at random from the remaining pack. Find the probability of getting
(i) a red card
(ii) a face card
(iii) a diamond or a club
(iv) a queen or a spade.
Solution:
Total number of cards = 52
Black jacks, black kings and black aces are removed
Now number of cards = 52 – (2 + 2 + 2) = 52 – 6 = 46
One card is drawn
(i) No. of red cards = 13 + 13 = 26
∴Probability = \(\\ \frac { 26 }{ 46 } \) = \(\\ \frac { 13 }{ 23 } \)
(ii) Face cards = 4 queens, 2 red jacks, 2 kings = 8
∴Probability = \(\\ \frac { 8 }{ 46 } \) = \(\\ \frac { 4 }{ 23 } \)
(iii) a diamond on a club = 13 + 10 = 23
∴Probability = \(\\ \frac { 23 }{ 46 } \) = \(\\ \frac { 1 }{ 2 } \)
(iv) A queen or a spade = 4 + 10 = 14
∴Probability = \(\\ \frac { 14 }{ 46 } \) = \(\\ \frac { 7 }{ 23 } \)
Question 16.
Two different dice are thrown simultaneously. Find the probability of getting:
(i) sum 7
(ii) sum ≤ 3
(iii) sum ≤ 10
Solution:
(i) Numbers whose sum is 7 will be (1, 6), (2, 5), (4, 3), (5, 2), (6, 1), (3, 4) = 6
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 6 }{ 36 } \) = \(\\ \frac { 1 }{ 6 } \)
(ii) Sum ≤ 3
Then numbers can be (1, 2), (2, 1), (1, 1) which are 3 in numbers
∴Probability will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 3 }{ 36 } \) = \(\\ \frac { 1 }{ 12 } \)
(iii) Sum ≤ 10
The numbers can be,
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, .6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5),
(6, 1), (6, 2), (6, 3), (6, 4) = 33
Probability will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \) = \(\\ \frac { 33 }{ 36 } \) = \(\\ \frac { 11 }{ 12 } \)
Question 17.
Two dice are thrown together. Find the probability that the product of the numbers on the top of two dice is
(i) 6
(ii) 12
(iii) 7
Solution:
Two dice are thrown together
Total number of events = 6 × 6 = 36
(i) Product 6 = (1, 6), (2, 3), (3, 2). (6, 1) = 4
Probability = \(\\ \frac { 4 }{ 36 } \) = \(\\ \frac { 1 }{ 9 } \)
(ii) Product 12 = (2, 6), (3, 4), (4, 3), (6, 2) = 4
Probability = \(\\ \frac { 4 }{ 36 } \) = \(\\ \frac { 1 }{ 9 } \)
(iii) Product 7 = 0 (no outcomes)
Probability = \(\\ \frac { 0 }{ 36 } \) = 0
We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test, drop a comment below and we will get back to you at the earliest.