ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test
Choose the correct answer from the given four options (1 to 16):
Question 1.
If the classes of a frequency distribution are 1-10, 11-20, 21-30, …, 51-60, then the size of each class is
(a) 9
(b) 10
(c) 11
(d) 5.5
Solution:
In the classes 1-10, 11-20, 21-30, …, 51-60,
the size of each class is 10. (b)
Question 2.
If the classes of a frequency distribution are 1-10, 11-20, 21-30,…, 61-70, then the upper limit of the class 11-20 is
(a) 20
(b) 21
(c) 19.5
(d) 20.5
Solution:
In the classes of distribution, 1-10, 11-20, 21-30, …, 61-70,
upper limit of 11-20 is 20-5 as the classes after adjustment are
0.5-10.5, 10.5-20.5, 20.5-30.5, … (d)
Question 3.
If the class marks of a continuous frequency distribution are 22, 30, 38, 46, 54, 62, then the class corresponding to the class mark 46 is
(a) 41.5-49.5
(b) 42-50
(c) 41-49
(d) 41-50
Solution:
The class marks of distribution are 22, 30, 38, 46, 54, 62,
then classes corresponding to these class marks 46 is
46.4 – 4 = 42, 46 + 4 = 50
(Class intervals is 8 as 30 – 22 = 8, 38 – 30 = 8
i.e:, 42 – 50 (b)
Question 4.
If the mean of the following distribution is 2.6,
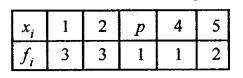
then the value of P is
(a) 2
(b) 3
(c) 2.6
(d) 2.8
Solution:
Mean = 2.6
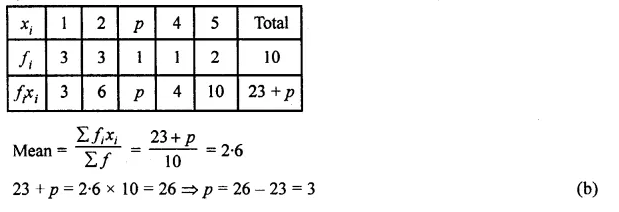
Question 5.
The measure of central tendency of statistical data which takes into account all the data is
(a) mean
(b) median
(c) mode
(d) range
Solution:
A measure of central tendency of statistical data is mean. (a)
Question 6.
In a grouped frequency distribution, the mid-values of the classes are used to measure which of the following central tendency?
(a) median
(b) mode
(c) mean
(d) all of these
Solution:
In a grouped frequency distribution,
the mid-values of the classes are used to measure Mean (c)
Question 7.
In the formula: \(\overline { x } =a+\frac { \sum { { f }_{ i }{ d }_{ i } } }{ \sum { { f }_{ i } } } \) for finding the mean of the grouped data, d’is are deviations from a (assumed mean) of
(a) lower limits of the classes
(b) upper limits of the classes
(c) mid-points of the classes
(d) frequencies of the classes
Solution:
The formula \(\overline { x } =a+\frac { \sum { { f }_{ i }{ d }_{ i } } }{ \sum { { f }_{ i } } } \) is the finding of mean of the grouped data, d’is are mid-points of the classes
Question 8.
In the formula: \(\overline { x } =a+c\left( \frac { \sum { { f }_{ i }{ u }_{ i } } }{ \sum { { f }_{ i } } } \right) \), for finding the mean of grouped frequency distribution, ui =
(a) \(\frac { { y }_{ i }+a }{ c } \)
(b) \(c({ y }_{ i }-a)\)
(c) \(\frac { { y }_{ i }-a }{ c } \)
(d) \(\frac { a-{ y }_{ i } }{ c } \)
Solution:
In \(\overline { x } =a+c\left( \frac { \sum { { f }_{ i }{ u }_{ i } } }{ \sum { { f }_{ i } } } \right) \),
for finding the mean of grouped frequency, ui is \(\frac { { y }_{ i }-a }{ c } \)(c)
Question 9.
While computing mean of grouped data, we assumed that the frequencies are
(a) evenly distributed over all the classes
(b) centred at the class marks of the classes
(c) centred at the upper limits of the classes
(d) centred at the lower limits of the classes
Solution:
For computing mean of grouped data,
we assumed that frequencies are centred at class marks of the classes. (b)
Question 10.
Construction of a cumulative frequency distribution table is useful in determining the
(a) mean
(b) median
(c) mode
(d) all the three measures
Solution:
Construction of a cumulative frequency distribution table
is used for determining the median, (b)
Question 11.
The times, in seconds, taken by 150 athletes to run a 110 m hurdle race are tabulated below:

The number of athletes who completed the race in less than 14.6 seconds is
(a) 11
(b) 71
(c) 82
(d) 130
Solution:
Time taken in seconds by 150 athletes to run a 110 m hurdle race as given in the sum,
the number of athletes who completed the race in less then 14.6 second is
2 + 4 + 5 + 71 = 82 athletes. (c)
Question 12.
Consider the following frequency distribution:

The upper limit of the median class is
(a) 17
(b) 17.5
(c) 18
(d) 18.5
Solution:
From the given frequency upper limit of median class is 17.5
as total frequencies 13 + 10 + 15 + 8 + 11 = 57
\(\\ \frac { 57+1 }{ 2 } \) = \(\\ \frac { 58 }{ 2 } \) = 29
and 13 + 10 + 15 = 28 where class is 12-17
But actual class will be 11.5-17.5
Upper limit is 17.5 (b)
Question 13.
Daily wages of a factory workers are recorded as:

The lower limit of the modal class is
(a) Rs 137
(b) Rs 143
(c) Rs 136.5
(d) Rs 142.5
Solution:
In the daily wages of workers of a factory are 131-136, 137-142, 142-148, …
which are not a proper class
So, proper class will be 130.5-136.5, 136.5-142.5, 142.5-148.5, …
Lower limit of a model class is 136.5 as 136.5-142.5 is the modal class. (c)
Question 14.
For the following distribution:

The sum of lower limits of the median class and modal class is
(a) 15
(b) 25
(c) 30
(d) 35
Solution:
From the given distribution
Sum of frequencies = 10 + 15 + 12 + 20 + 9 = 66
and median is \(\\ \frac { 66 }{ 2 } \) = 33
Median class will be 10-15 and modal class is 15-20
Sum of lower limits = 10 + 15 = 25 (b)
Question 15.
Consider the following data:

The difference of the upper limit of the median class and the lower limit of the modal class is
(a) 0
(b) 19
(c) 20
(d) 38
Solution:
From the given data
Total frequencies = 4 + 5 + 13 + 20 + 14 + 7 + 4 = 67
Median class \(\\ \frac { 67+1 }{ 2 } \) = 34
which is (4 + 5 + 13 + 20) 125-145 and modal class is 125-145
Difference of upper limit of median class and the lower limit of the modal class
= 145 – 125 = 20 (c)
Question 16.
An ogive curve is used to determine
(a) range
(b) mean
(c) mode
(d) median
Solution:
An ogive curve is used to find median. (d)
We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS, drop a comment below and we will get back to you at the earliest.