ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test
Question 1.
Arun scored 36 marks in English, 44 marks in Civics, 75 marks in Mathematics and x marks in Science. If he has scored an average of 50 marks, find x.
Solution:
Marks in English = 36
Marks in Civics = 44
Marks in Mathematics = 75
Marks in Science = x
Total marks in 4 subjects = 36 + 44 + 75 + x = 155 + x
average marks = \(\\ \frac { 155+x }{ 4 } \)
But average marks = 50 (given)
\(\\ \frac { 155+x }{ 4 } \) = 50
⇒ 155 + x = 200
⇒ x = 200 – 155 = 45
Question 2.
The mean of 20 numbers is 18. If 3 is added to each of the first ten numbers, find the mean of new set of 20 numbers.
Solution:
Mean of 20 numbers =18
Total number = 18 × 20 = 360
By adding 3 to first 10 numbers,
The new sum will be = 360 + 3 × 10 = 360 + 30 = 390
New Mean = \(\\ \frac { 390 }{ 20 } \) = 19.5
Question 3.
The average height of 30 students is 150 cm. It was detected later that one value of 165 cm was wrongly copied as 135 cm for computation of mean. Find the correct mean.
Solution:
In first case,
Average height of 30 students = 150 cm
Total height = 150 × 30 = 4500 cm
Difference in copying the number = 165 – 135 = 30 cm
Correct sum = 4500 + 30 = 4530 cm
Correct mean = \(\\ \frac { 4530 }{ 30 } \) = 151 cm
Question 4.
There are 50 students in a class of which 40 are boys and the rest girls. The average weight of the students in the class is 44 kg and average weight of the girls is 40 kg. Find the average weight of boys.
Solution:
Total students of a class = 50
No. of boys = 40
No. of girls = 50 – 40 = 10
Average weight of 50 students = 44 kg
Total weight = 44 × 50 = 2200 kg
Average weight of 10 girls = 40 kg
.’. Total weight of girls = 40 × 10 = 400 kg
Then the total weight of 40 boys = 2200 – 400 = 1800kg
Average weight of boys = \(\\ \frac { 1800 }{ 40 } \) = 45kg
Question 5.
The contents of 50 boxes of matches were counted giving the following results

Calculate the mean number of matches per box.
Solution:
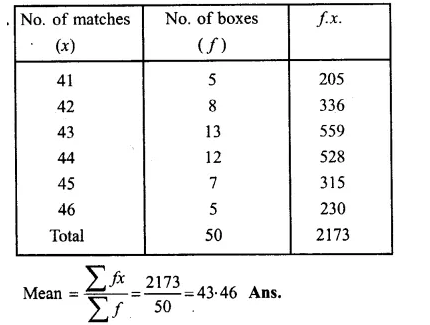
Question 6.
The heights of 50 children were measured (correct to the nearest cm) giving the following results :

Solution:
Calculate the mean height for this distribution correct to one place of decimal.
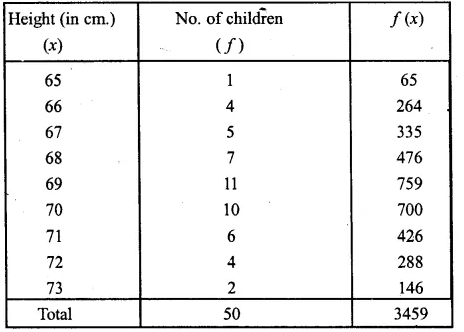
Mean = \(\frac { \sum { fx } }{ \sum { f } } =\frac { 3459 }{ 50 } \) = 69.18 = 69.2
Question 7.
Find the value of p for the following distribution whose mean is 20.6 :

Solution:

Question 8.
Find the value of p if the mean of the following distribution is 18.

Solution:

Question 9.
Find the mean age in years from the frequency distribution given below:

Solution:
Arranging the classes in proper form
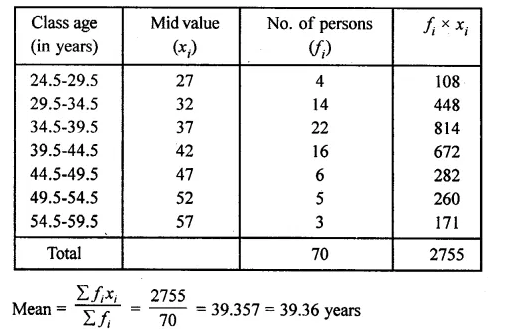
Question 10.
Calculate the Arithmetic mean, correct to one decimal place, for the following frequency distribution :

Solution:
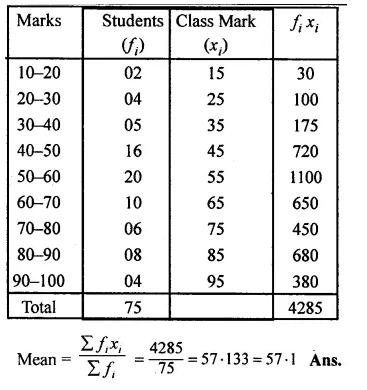
Question 11.
The mean of the following frequency distribution is 62.8. Find the value of p.

Solution:
Mean = 62.8

Hence p = 10
Question 12.
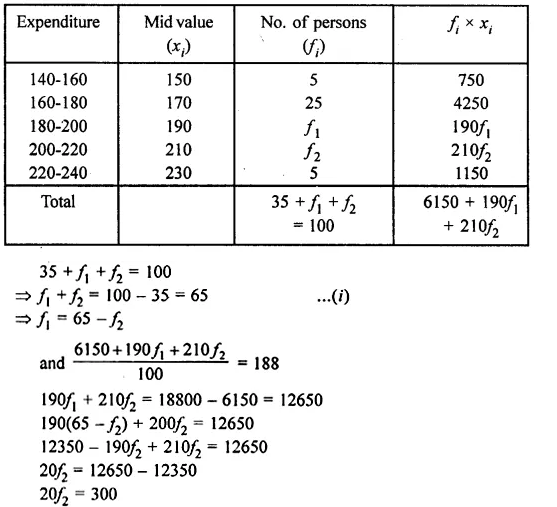
The daily expenditure of 100 families are given below. Calculate f1, and f2, if the mean daily expenditure is Rs 188.

Solution:
Mean = 188,
No. of families = 100
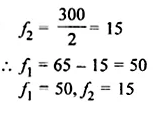
Question 13.
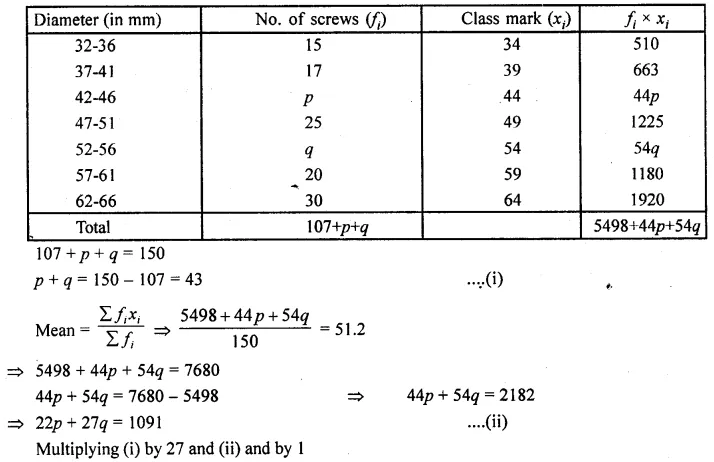
The measures of the diameter of the heads of 150 screw is given in the following table. If the mean diameter of the heads of the screws is 51.2 mm, find the values of p and q

Solution:
Mean = 51.2
No. of screws = 150
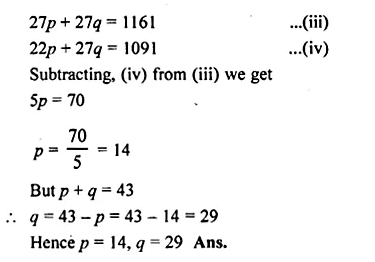
Question 14.
The median of the following numbers, arranged in ascending order is 25. Find x, 11, 13, 15, 19, x + 2, x + 4, 30, 35, 39, 46
Solution:
Here, n = 10, which is even
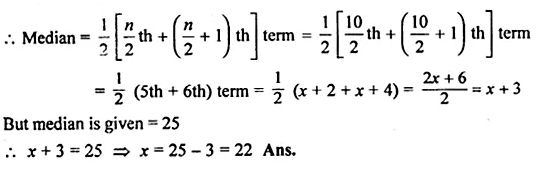
Question 15.
If the median of 5, 9, 11, 3, 4, x, 8 is 6, find the value of x.
Solution:
Arranging in ascending order, 3, 4, 5, x, 8, 9, 11,
Here n = 7 which is odd.
∴ Median = \(\\ \frac { n+1 }{ 2 } \) th term = \(\\ \frac { 7+1 }{ 2 } \) = 4th term = x
∴ but median = 6
∴ x = 6
Question 16.
Find the median of: 17, 26, 60, 45, 33, 32, 29, 34, 56 If 26 is replaced by 62, find the new median.
Solution:
Arranging the given data in ascending order
17, 26, 29, 32, 33, 34, 45, 56, 60
Here n = 9 which is odd
∴Median = \(\\ \frac { n+1 }{ 2 } \) th term = \(\\ \frac { 9+1 }{ 2 } \) = \(\\ \frac { 10 }{ 2 } \) = 5th term = 33
(ii) If 26 is replaced by 62, their the order will be
17, 29, 32, 33, 34, 45, 56, 60, 62
Here 5th term is 34
∴ Median = 34
Question 17.
The marks scored by 16 students in a class test are : 3, 6, 8, 13, 15, 5, 21, 23, 17, 10, 9, 1, 20, 21, 18, 12
Find
(i) the median
(ii) lower quartile
(iii) upper quartile
Solution:
Arranging the given data in ascending order:
1, 3, 5, 6, 8, 9, 10, 12, 13, 15, 17, 18, 20, 21, 21, 23
Here n = 16 which is even.
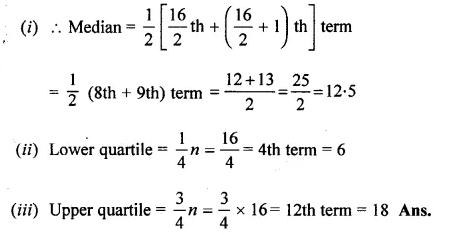
Question 18.
Find the median and mode for the set of numbers : 2, 2, 3, 5, 5, 5, 6, 8, 9
Solution:
Here n = 9 which is odd.
∴Median = \(\\ \frac { n+1 }{ 2 } \) th term = \(\\ \frac { 9+1 }{ 2 } \) = \(\\ \frac { 10 }{ 2 } \) = 5th term = 5
Here 5 occur maximum times
∴Mode = 5
Question 19.
Calculate the mean, the median and the mode of the following distribution :

Solution:

Question 20.
The daily wages of 30 employees in an establishment are distributed as follows :

Estimate the modal daily wages for this distribution by a graphical method.
Solution:
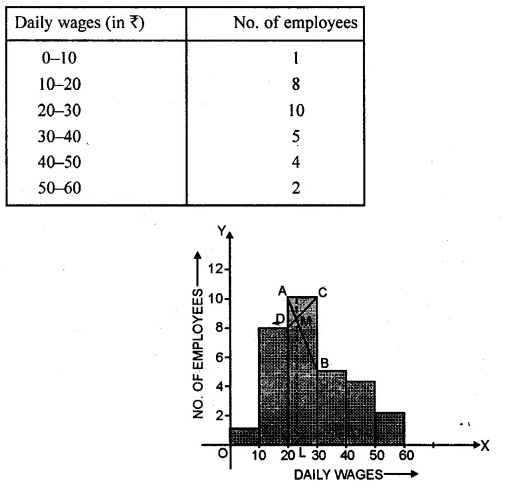
Taking daily wages on x-axis and No. of employees on the y-axis
and draw a histogram as shown. Join AB and CD intersecting each other at M.
From M draw ML perpendicular to x-axis, L is the mode
∴ Mode = Rs 23
Question 21.
Using the data given below, construct the cumulative frequency table and draw the ogive. From the ogive, estimate ;
(i) the median
(ii) the inter quartile range.

Also state the median class
Solution:
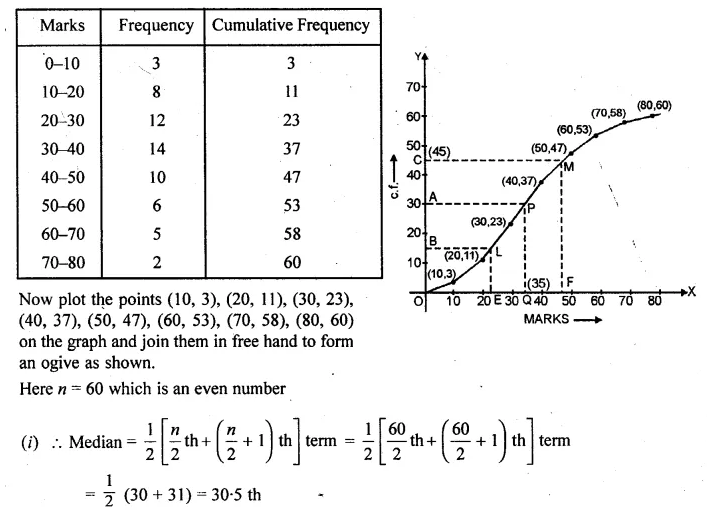

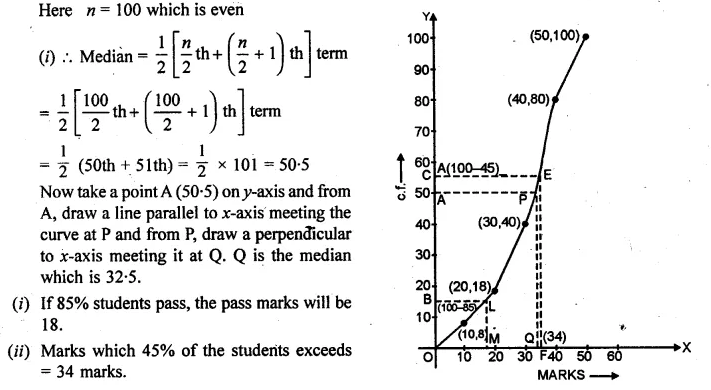
Question 22.
Draw a cumulative frequency curve for the following data :

Hence determine:
(i) the median
(ii) the pass marks if 85% of the students pass.
(iii) the marks which 45% of the students exceed.
Solution:

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test, drop a comment below and we will get back to you at the earliest.