ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5
More Exercise
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test
Question 1.
The diameter of a metallic sphere is 6 cm. The sphere is melted and drawn into a wire of uniform cross-section. If the length of the wire is 36 m, find its radius.
Solution:
Diameter of metallic sphere = 6 cm
Radius(r) = \(\\ \frac { 6 }{ 2 } \) = 3cm

Question 2.
The radius of a sphere is 9 cm. It is melted and drawn into a wire of diameter 2 mm. Find the length of the wire in metres.
Solution:
Radius of sphere = 9 cm
Volume = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }=\frac { 4 }{ 3 } \pi \times { \left( 9 \right) }^{ 3 }{ cm }^{ 3 }\)
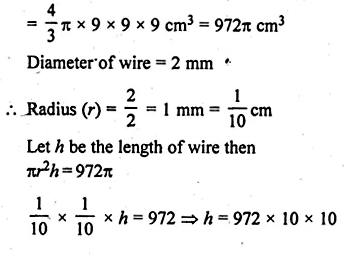
h = 97200 cm = 972 m
Length of wire = 972 m
Question 3.
A solid metallic hemisphere of radius 8 cm is melted and recasted into right circular cone of base radius 6 cm. Determine the height of the cone.
Solution:
Radius of a solid hemisphere (r) = 8 cm
Volume = \(\frac { 2 }{ 3 } \pi { r }^{ 3 }=\frac { 2 }{ 3 } \pi \times { \left( 8 \right) }^{ 3 }{ cm }^{ 3 }\)

Question 4.
A rectangular water tank of base 11 m x 6 m contains water upto a height of 5 m. if the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
Solution:
Base of a water tank = 11 m × 6 m
Height of water level in it (h) = 5 m
Volume of water =11 × 6 × 5 = 330 m³
Volume of water in the cylindrical tank
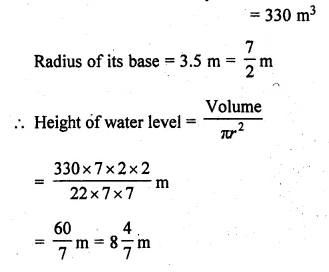
Question 5.
The rain water from a roof of dimensions 22 m x 20 m drains into a cylindrical vessel having diameter of base 2 m and height; 3.5 m. If the rain water collected from the roof just fill the cylindrical vessel, then find the rainfall in cm.
Solution:
Dimensions of roof = 22 m × 20 m
Let rainfall = x m
.’. Volume of water = 22 × 20 × x m³
Volume of water in cylinder = 22 × 20 × x m³
Diameter of its base = 2 m

Question 6.
The volume of a cone is the same as that of the cylinder whose height is 9 cm and diameter 40 cm. Find the radius of the base of the cone if its height is 108 cm.
Solution:
Diameter of a cylinder = 40 cm
Radius (r) = \(\\ \frac { 40 }{ 2 } \) = 20 cm
Height(h) = 9 cm

Question 7.
Eight metallic spheres, each of radius 2 cm, are melted and cast into a single sphere. Calculate the radius of the new (single) sphere.
Solution:
Radius of each metallic sphere (r) = 2 cm
Volume of one sphere = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)
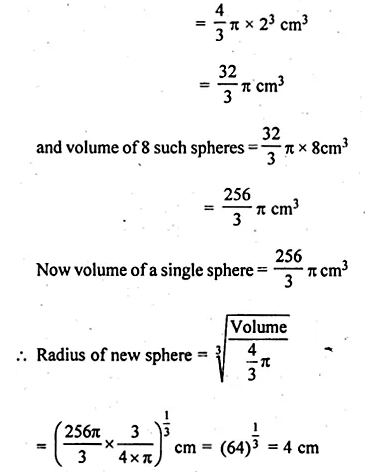
Question 8.
A metallic disc, in the shape of a right circular cylinder, is of height 2.5 mm and base radius 12 cm. Metallic disc is melted and made into a sphere. Calculate the radius of the sphere.
Solution:
Height of disc cylindrical shaped = 2.5 mm
and base radius = 12 cm
Volume of the disc = πr²h

Question 9.
Two spheres of the same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the big sphere.
Solution:
Weight of first sphere = 1 kg
and weight of second sphere = 7 kg
Radius of smaller sphere = 3 cm
Let r be the radius of a larger sphere
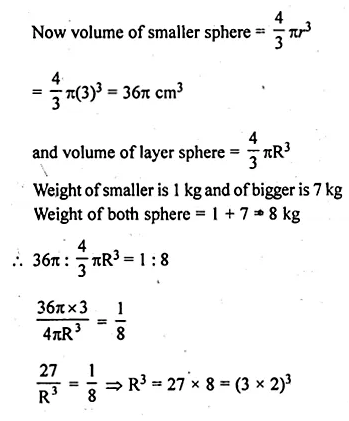
R = 3 x 2 = 6 cm
Diameter of big sphere = 2 x 6 = 12 cm
Question 10.
A hollow copper pipe of inner diameter 6 cm and outer diameter 10 cm is melted and changed into a solid circular cylinder of the same height as that of the pipe. Find the diameter of the solid cylinder.
Solution:
Inner diameter of a hollow pipe = 6 cm
and outer diameter = 10 cm
Inner radius (r) = \(\\ \frac { 6 }{ 2 } \) = 3cm

Question 11.
A solid sphere of radius 6 cm is melted into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm and height is 72 cm, find the uniform thickness of the cylinder.
Solution:
Radius of a solid sphere (r) = 6 cm
Volume = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }=\frac { 4 }{ 3 } \pi \times { \left( 6 \right) }^{ 3 }{ cm }^{ 3 }\)

Question 12.
A hollow metallic cylindrical tube has an internal radius of 3 cm and height 21 cm. The thickness of the metal of the tube is \(\\ \frac { 1 }{ 2 } \) cm. The tube is melted and cast into a right circular cone of height 7 cm. Find the radius of the cone correct to one decimal place.
Solution:
Internal radius of a hollow metallic cylindrical tube (r) = 3 cm
and height (h) = 21 cm

Question 13.
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively, is melted into a cone of base diameter 8 cm. Find the height of the cone. (2002)
Solution:
Internal diameter of a hollow sphere = 4 cm
and external diameter = 8 cm
Internal radius (r) = 2 cm
and external radius (R) = 4 cm
Volume of hollow sphere

Question 14.
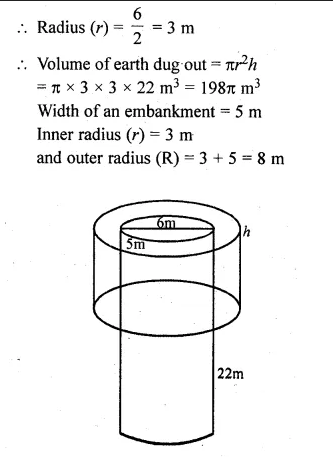
A well with inner diameter 6 m is dug 22 m deep. Soil taken out of it has been spread evenly all round it to a width of 5 m to form an embankment. Find the height of the embankment.
Solution:
Inner diameter of a well = 6 m
Depth (h) = 22 m

Question 15.
A cylindrical can of internal diameter 21 cm contains water. A solid sphere whose diameter is 10.5 cm is lowered into the cylindrical can. The sphere is completely immersed in water. Calculate the rise in water level, assuming that no water overflows.
Solution:
Internal diameter of cylindrical can = 21 cm
Radius (R) = \(\\ \frac { 21 }{ 2 } \) cm
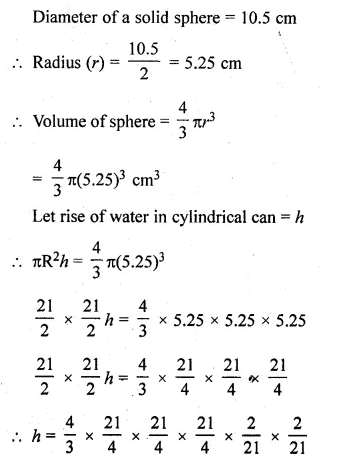
Question 16.
There is water to a height of 14 cm in a cylindrical glass jar of radius 8 cm. Inside the water there is a sphere of diameter 12 cm completely immersed. By what height will the water go down when the sphere is removed?
Solution:
Radius of the cylindrical jar (R) = 8 cm
Height of water level (h) = 14 cm
Volume of water = πR²h

Question 17.
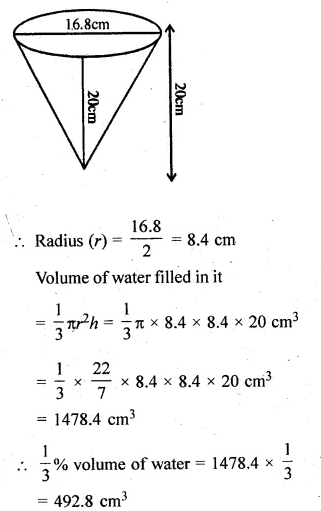
A vessel in the form of an inverted cone is filled with water to the brim. Its height is 20 cm and diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one-third of the water in the original cone overflows. What is the volume of each of the solid cone submerged? (2002)
Solution:
Height of conical vessel (h) = 20 cm
and diameter = 16.8 cm
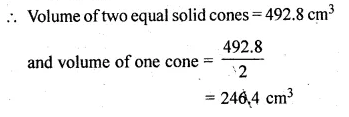
Question 18.
A solid metallic circular cylinder of radius 14 cm and height 12 cm is melted and recast into small cubes of edge 2 cm. How many such cubes can be made from the solid cylinder?
Solution:
Radius of a solid metallic cylindrical (r) = 14 cm
and height (h) = 12 cm
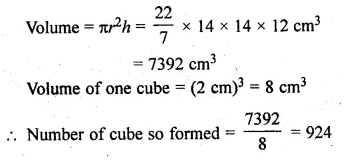
Question 19.
How many shots each having diameter 3 cm can be made from a cuboidal lead solid of dimensions 9 cm x 11 cm x 12 cm?
Solution:
Diameter of a shot = 3 cm
Radius (r) = \(\\ \frac { 3 }{ 2 } \) cm
Volume of one shot = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)

Question 20.
How many spherical lead shots of diameter 4 cm can be made out of a solid cube of lead whose edge measures 44 cm?
Solution:
Diameter of lead shot = 4 cm
Radius (r) = \(\\ \frac { 4 }{ 2 } \) = 2 cm and
volume =\(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)

Question 21.
Find the number of metallic circular discs with 1.5 cm base diameter and height 0.2 cm to be melted to form a circular cylinder of height 10 cm and diameter 4.5 cm.
Solution:
Radius of the circular disc (r) = 0.75 cm
Height of circular disc (h) = 0.2 cm
Radius of cylinder (R) = 2.25 cm
Height of cylinder (H) = 10 cm
Now,
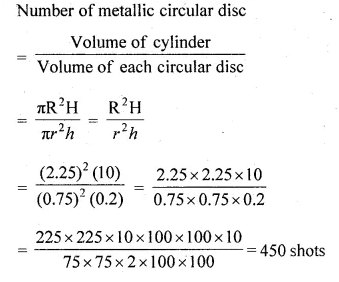
Question 22.
A solid metal cylinder of radius 14 cm and height 21 cm is melted down and recast into spheres of radius 3.5 cm. Calculate the number of spheres that can be made.
Solution:
Radius of a solid metallic cylinder (r) = 14 cm
and height (h) = 21 cm
Volume of cylinder = πr²h
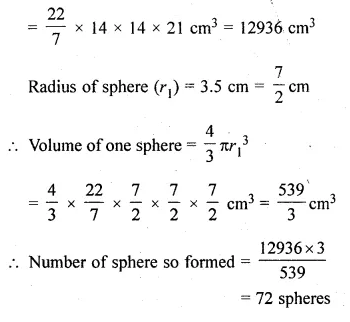
Question 23.
A metallic sphere of radius 10.5 cm is melted and then recast into small cenes, each of radius 3.5 cm and height 3 cm. Find the number of cones thus obtained. (2005)
Solution:
Radius of a metallic sphere (r) = 10.5 cm
Volume = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)
= \(\\ \frac { 4 }{ 3 } \) × π × 10.5 × 10.5 × 10.5 = 1543.5π cm³

Question 24.
A certain number of metallic cones each of radius 2 cm and height 3 cm are melted and recast in a solid sphere of radius 6 cm. Find the number of cones. (2016)
Solution:
Radius of each cone (r) = 2 cm
and height (h) = 3 cm
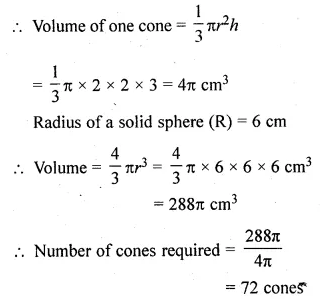
Question 25.
A vessel is in the form of an inverted cone. Its height is 11 cm and the radius of its top, which is open, is 2.5 cm. It is filled with water upto the rim. When some lead shots, each of which is a sphere of radius 0.25 cm, are dropped into the vessel, \(\\ \frac { 2 }{ 5 } \) of the water flows out. Find the number of lead shots dropped into the vessel. (2003)
Solution:
Radius of the top of the inverted conical vessel (R) = 2.5 cm
and height (h)= 11 cm
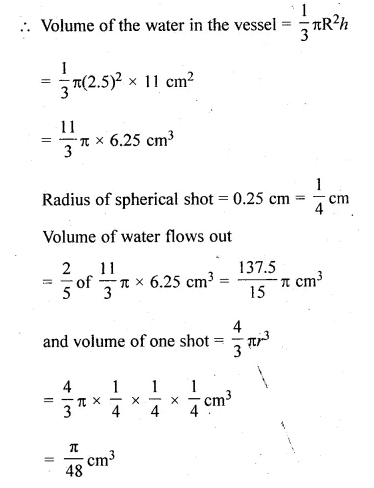

Question 26.
The surface area of a solid metallic sphere is 616 cm². It is melted and recast into smaller spheres of diameter 3.5 cm. How many such spheres can be obtained? (2007)
Solution:
Surface area of a metallic sphere = 616 cm²

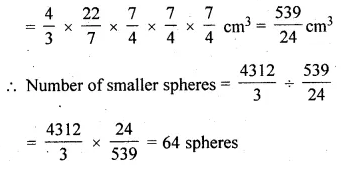
Question 27.
The surface area of a solid metallic sphere is 1256 cm². It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate
(i) the radius of the solid sphere.
(ii) the number of cones recast. (Use π = 3.14).
Solution:
Surface area of a solid metallic sphere = 1256 cm²

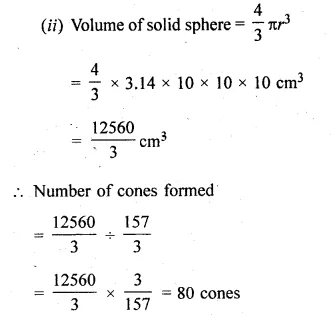
Question 28.
Water is flowing at the rate of 15 km/h through a pipe of diameter 14 cm into a cuboid pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
Solution:
Speed of water flow = 15 km/h
Diameter of pipe = 14 cm

Question 29.
A cylindrical can whose base is horizontal and of radius 3.5 cm contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate :
(i) the total surface area of the can in contact with water when the sphere is in it.
(ii) the depth of the water in the can before the sphere was put into the can. Given your answer as proper fractions.
Solution:
Radius of a cylindrical can = 3.5 cm
Radius of the sphere = 3.5 cm
and height of water level in the can = 3.5 × 2 = 7 cm

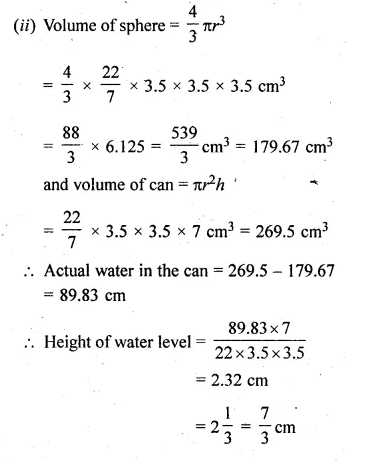
We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5, drop a comment below and we will get back to you at the earliest.