ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Ex 14
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Ex 14
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Ex 14
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Chapter Test
Question 1.
A point moves such that its distance from a fixed line AB is always the same. What is the relation between AB and the path traveled by P ?
Solution:
Let point P moves in such a way that
it is at a fixed distance from the fixed line AB.
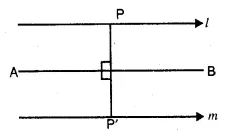
∴ It is a set of two lines l and m parallel to AB
drawn on either side of it at equal distance from it.
Question 2.
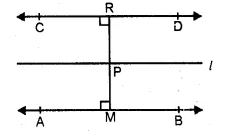
A point P moves so that its perpendicular distance from two given lines AB and CD are equal. State the locus of the point P.
Solution:
(i) When two lines AB and CD are parallel,
then the locus of the point P which is equidistant
from AB and CD is a line (l)
in the midway of AB and CD and parallel to them
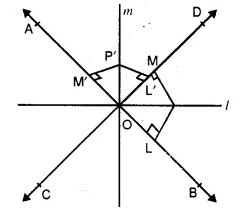
(ii) If AB and CD are intersecting lines,
then the locus of the point P will be a
pair of the straight lines l and m which bisect
the angles between the given lines AB and CD.
Question 3.
P is a fixed point and a point Q moves such that the distance PQ is constant, what is the locus of the path traced out by the point Q ?
Solution:
∴ P is a fixed point and Q is a moving point
such that it is always at an equidistant from P.
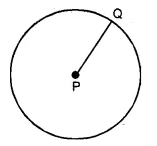
∴ P is the centre of the path of Q which is a circle.
The distance between P and Q is the radius of the circle.
Hence locus of point Q is a circle with P as centre.
Question 4.
(i) AB is a fixed line. State the locus of the point P so that ∠APB = 90°.
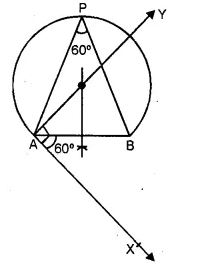
(ii) A, B are fixed points. State the locus of the point P so that ∠APB = 60°.
Solution:
(i) AB is a fixed line and P is a point
such that ∠APB = 90°.
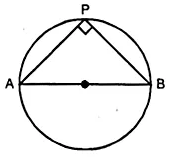
The locus of P will be the circle whose diameter is AB.
We know that the angle in a semi-circle is always equal to 90°.
∠APB = 90°
(ii) AB is a fixed line and P is a point such that ∠APB = 60°.
The locus of P will be a major segment of a circle whose AB is a chord.
Question 5.
Draw and describe the locus in each of the following cases :
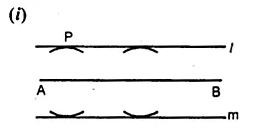
(i) The locus of points at a distance 2.5 cm from a fixed line.
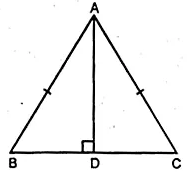
(ii) The locus of vertices of all isosceles triangles having a common base.
(iii) The locus of points inside a circle and equidistant from two fixed points on the circle.
(iv) The locus of centres of all circles passing through two fixed points.
(v) The locus of a point in rhombus ABCD which is equidistant from AB and AD. (1998)
(vi) The locus of a point in the rhombus ABCD which is equidistant from points A and C.
Solution:
1. Draw a given line AB.
2. Draw lines of l and m parallel to AB at a distance of 2.5 cm.
Lines l and m are the locus of point P which is at a distance of 2.5 cm.
(ii) ∆ABC is an isosceles triangle in which AB = AC.
From A, draw AD perpendicular to BC.
AD is the locus of the point A the vertices of ∆ABC.
In rt. ∆ABD and ∆ACD
Side AD = AD (Common)
Hyp. AB = AC (given)
∴ ∆ABD = ∆ACD (R.H.S. Axiom)
∴ BD = DC (c.p.c.t.)
Hence locus of vertices of isosceles triangles
having common base is the perpendicular bisector of BC.
(iii) (i) Draw a circle with centre O.
(ii) Take points A and B on it and join them.
(iii) Draw a perpendicular bisector of AB
which passes from O and meets the circle at C.
CE the diameter, which is the locus of a point inside the circle
and equidistant from two points A and B at the circle.
(iv) Let C1, C2, C3 be the centres of the circle
which pass through the two fixed points A and B.
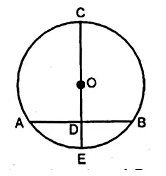
Draw a line XY passing through these centres C1, C2, C3.
Hence locus of centres of circles passing through two points A and B
is the perpendicular bisector of the line segment joining the two fixed points.
(v) In rhombus ABCD, Join AC.
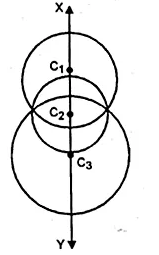
AC is the diagonal of rhombus ABCD
∴ AC bisect ∠A.
∴ Any point on AC, is the locus which is equidistant from AB and AD.
(vi) ABCD is a rhombus. Join BD
BD is the locus of a point in the rhombus which is equidistant from A and C.
Diagonal BD bisects ∠B and ∠D.
Any point on BD will be equidistant from A and C.
Question 6.
Describe completely the locus of points in each of the following cases :
(i) mid-point of radii of a circle.
(ii) centre of a ball, rolling along a straight line on a level floor.
(iii) point in a plane equidistant from a given line.
(iv) point in a plane, at a constant distance of 5 cm from a fixed point (in the plane).
(v) centre of a circle of varying radius and touching two arms of ∠ADC.
(vi) centre of a circle of varying radius and touching a fixed circle, centre O, at a fixed point A on it.
(vii) centre of a circle of radius 2 cm and touching a fixed circle of radius 3 cm with centre 0.
Solution:
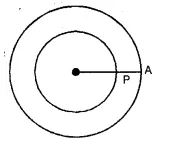
(i) The locus of midpoints of the radii of a circle
is another concentric circle with radius is
half of the radius of the given circle.
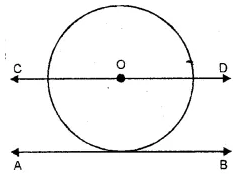
(ii) AB is the straight line on the ground and the ball is rolling on it
∴ locus of the centre of the ball is a line parallel A lo the given line AB.
(iii) AB is the given line and P is a point in the plane.
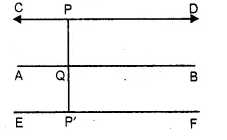
From P, draw a line CD and another line EF from P’ parallel to AB.
Thus CD and EF are the lines which are the locus of the point equidistant from AB
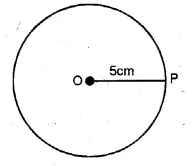
(iv) Take a point O and another point P such that OP = 5 cm.
with centre O and radius equal to OP, draw a circle.
Thus this circle is the locus of point P
which is at a distance of 5 cm from O, the given point.
(v) Draw the bisector BX of ∠ABC.
This bisector of an angle is the locus of the centre of a circle with different radii.
Any point on BX, is equidistant from the arms BA and BC of the ∠ABC.
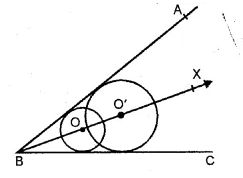
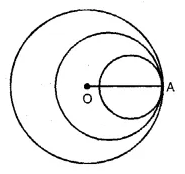
(vi) A circle with centre O is given and one point A on it.
The locus of the centre of a circle which touches the circle
at the fixed point A on it, is a line joining the points O and A.
(vii) (a) If the circle with 2 cm as radius touches the given circle
externally then the locus of the centre of the circle
will be a concentric circle with radius 3+2 = 5 cm.
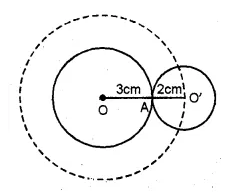
If the circle with 2 cm as radius touches the given circle with 3 cm as radius internally,
then the locus of the centre of the circle will be a concentric circle with radius 3-2 = 1 cm.
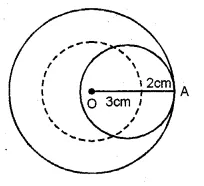
Question 7.
Using ruler and compasses construct :
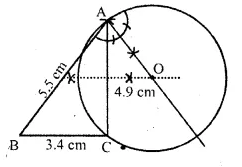
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of points equidistant from A and C.
Solution:
(i) Draw BC = 3.4 and mark the arcs of 5.5 add 4.9 cm from B and C.
Join A, B and C.
ABC is the required triangle.
(ii) Draw ⊥ bisector of AC.
(iii) Draw an angle of 90° at AB at A which intersects ⊥ bisector at O.
Draw circle taking 0 as centre and OA as the radius.
Question 8.
Construct triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that :
(i) P is equidistant from B and C and
(ii) P is equidistant from AB and BC
(iii) Measure and record the length of PB. (2000)
Solution:
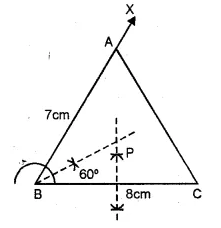
(i) Take BC = 8 cm a long line segment. At B,
draw a ray BX making an angle of 60° with BC.
Cut off BA = 7 cm. and join AC.
(i) Draw the perpendicular bisector of BC.
(ii) Draw the angle bisector of ∠B which intersect
the perpendicular bisector of BC at P. P is the required point.
(iii) On measuring the length of BP = 4.6 cm (approx.)
Question 9.
A straight line AB is 8 cm long. Locate by construction the locus of a point which is :
(i) Equidistant from A and B.
(ii) Always 4 cm from the line AB.
(iii) Mark two points X and Y, which are 4 cm from AB and equidistant from A and B. Name the figure AXBY.(2008)
Solution:
Steps of construction:
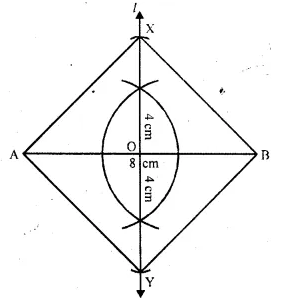
(i) Draw a line segment AB = 8 cm.
(ii) With the help of compasses and ruler,
draw the perpendicular bisector l of AB which intersects AB at O.
(iii) Then any point on l, is equidistant from A and B.
(iv) Cut off OX = OY = 4 cm. The X and Y are the required loci,
which is equidistant from AB and also from A and B.
(v) Join AX, XB, BY and YA.
The figures so formed AXBY is the shape of a square because
its diagonals are equal and bisect each other at right angles.
Question 10.
Use ruler and compasses only for this question.
(i) Construct ∆ABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure arid record the length of PB. (2010)
Solution:
In ∆ABC, AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°
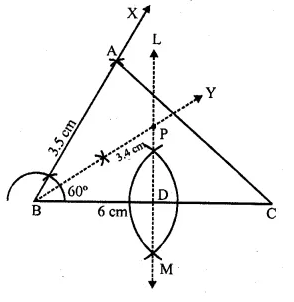
Steps of construction :
(a) (i) Draw a line segment BC = 6 cm
(ii) At, B draw a ray BX making an angle of 60° and cut off BA = 3.5 cm.
(iii) Join AC.
The ∆ABC is the required triangle.
(b) Draw the bisector BY of ∠ABC.
(c) Draw the perpendicular bisector of BC which intersects BY at P.
P is the required point P which is equidistant from BC and BA
and also equidistant from B and C.
On measuring PB it is 3.4 cm (approx)
Question 11.
Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°. Hence:
(i) Construct the locus of points equidistant from BA and BC.
(ii) Construct the locus of points equidistant from B and C.
(iii) Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
Solution:
Steps of construction :
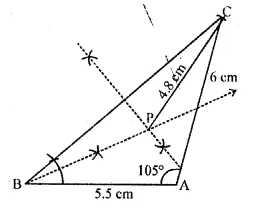
Construct the triangle ABC with AB = 5.5 cm
∠BAC = 105° and AC = 6 cm
(i) Points which are equidistant from BA and BC lies on the bisector of ∠ABC.
(ii) Points equidistant from B and C lies on the perpendicular bisector of BC.
Draw perpendicular bisector of BC.
The required point P is the point of intersection of the bisector of
∠ABC and the perpendicular bisector of BC.
(iii) Required length of PC = 4.8 cm.
Question 12.
In the given diagram, A, B and C are fixed collinear points; D is a fixed point outside the line: Locate

(i) the point P on AB such that CP = DP.
(ii) the points Q such that CQ = DQ = 3 cm. How many such points are possible?
(iii) the points R on AB such that DR = 4 cm. How many such points are possible?
(iv) the points S such that CS = DS and S is 4 cm away from the line CD. How many such points are possible?
(v) Are the points P, Q, R collinear?
(vi) Are the points P, Q, S collinear?
Solution:
Points A, B and C are collinear and D is any point outside AB.
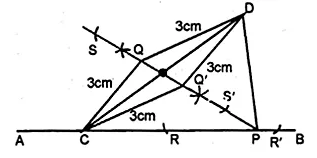
(i) Join CD.
(ii) Draw the perpendicular bisector of CD which meets AB in P.
(iii) P is the required point such that CP = DP
(iv) With centres C and D, draw two arcs with 3 cm radius
which intersect each other at Q and Q’.
Hence there are two points Q and Q’ which are equidistant from C and D.
(v) With centre D, and radius 4 cm draw an arc which intersects AB at R and R’
∴ R and R’ are the two point on AB.
(vi) With centre C and D, draw arcs with a radius equal to
4 cm which intersects each other in S and S’.
∴ There can be two such points which are equidistant from C and D.
(vii) No P, Q, R are not collinear.
(viii) Yes, P, Q, S are collinear.
Question 13.
Points A, B and C represent position of three towers such that AB = 60 m, BC = 73m and CA = 52 m. Taking a scale of 10 m to 1 cm, make an accurate drawing of ∆ABC. Find by drawing, the location of a point which is equidistant from A, B and C, and its actual distance from any of the towers.
Solution:
AB = 60 mm = 6.0 cm, BC = 73 mm = 7.3 cm
and CA = 52 mm = 5.2 cm.
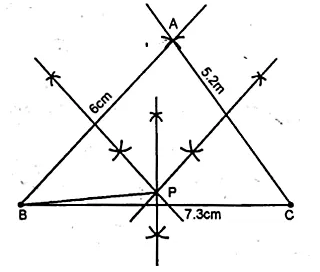
(i) Draw a line segment BC = 7.3cm
(ii) With Centre B and radius 6cm and with centre C
and radius 5.2 cm, draw two arcs intersecting each other at A
(iii) Joining AB and AC.
(iv) Draw the perpendicular bisector of AB, BC and CA respectively,
which intersect each other at point P. Join PB.
P is equidistant from A, B and C on measuring PB = 3.7 cm.
Actual distance = 37 m.
Question 14.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these lines and also 2 cm away from their point of intersection. How many such points exist ? (1990)
Solution:
(i) Two lines AB and CD intersect each other at O.
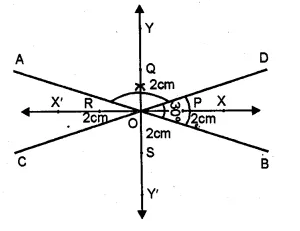
(ii) Draw the bisector of ∠BOD and ∠AOD
(iii) With centre O and radius equal to 2 cm.
marks points on the bisector of angles at P, Q, R and S respectively.
Hence there are four points which are equidistant
from AB and CD and 2 cm from 0, the point of intersection of AB and CD.
Question 15.
Without using set square or protractor, construct the quadrilateral ABCD in which ∠BAD = 45°, AD = AB = 6 cm, BC = 3.6 cm and CD = 5 cm.
(i) Measure ∠BCD.
(ii) Locate the point P on BD which is equidistant from BC and CD. (1992)
Solution:
(i) Take AB = 6 cm long
(ii) AT A, draw the angle of 45° and cut off AD = 6 cm
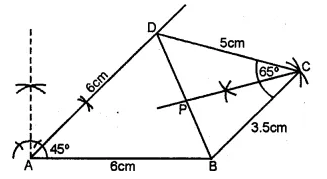
(iii) With centre D and radius 5 cm and with centre B,
and radius 3.5 cm draw two arcs intersecting each other at C.
(iv) Join CD and CB and join BD
ABCD is the required quadrilateral.
(v) On measuring ∠BCD = 65°.
(vi) Draw the bisector of ∠BCD which intersects BD at P.
P is the required point which is equidistant from CD and CB.
Question 16.
Without using set square or protractor, construct rhombus ABCD with sides of length 4 cm and diagonal AC of length 5 cm. Measure ∠ABC. Find the point R on AD such that RB = RC. Measure the length of AR. (1990)
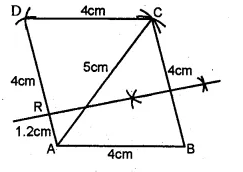
Solution:
(i) Take AB = 4 cm
(ii) With centre A, draw an arc of 5 cm radius
and with B draw another arc of radius 4 cm intersecting each other at C.
(iii) Join AC and BD.
(iv) Again with centre A and C,
draw two arcs of radius 4 cm intersecting each other on D.
(v) Join AD and CD.
ABCD is the required rhombus and on measuring the ∠ABC, it is 78°.
(vi) Draw perpendicular bisector of BC intersecting AD at R.
On measuring the length of AR, it is equal to 1.2 cm.
Question 17.
Without using set-squares or protractor construct :
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC. (1994)
Solution:
Steps of Construction :
(i) Draw BC = 3.2 cm long.
(ii) With centre B and radius 5.5 cm
and with centre C and radius 4.8 cm
draw arcs intersecting each other at A.
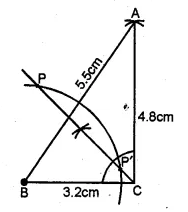
(iiii) Join AB and AC.
(iv) Draw the bisector of ∠BCA.
(v) With centre B and radius 2.5 cm,
draw an arc intersecting the angle bisector of ∠BCA at P and P’.
P and P’ are two loci which satisfy the given condition.
On measuring CP and CP’
CP = 3.6 cm and CP’ =1.1 cm.
Question 18.
By using ruler and compasses only, construct an isosceles triangle ABC in which BC = 5 cm, AB = AC and ∠BAC = 90°. Locate the point P such that :
(i) P is equidistant from the sides BC and AC.
(ii) P is equidistant from the points B and C.
Solution:
Steps of Construction :
(i) Take BC = 5.0 cm and bisect it at D.
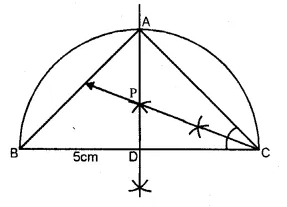
(ii) Taking BC as diameter, draw a semicircle.
(iii) At D, draw a perpendicular intersecting the circle at A
(iv) Join AB and AC.
(v) Draw the angle bisector of C intersecting
the perpendicular at P. P is the required point.
Question 19.
Using ruler and compasses only, construct a quadrilateral ABCD in which AB = 6 cm, BC = 5 cm, ∠B = 60°, AD = 5 cm and D is equidistant from AB and BC. Measure CD. (1983)
Solution:
Steps of Construction :
(i) Draw AB = 6 cm
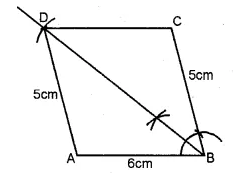
(ii) At B, draw angle of 60° and cut off BC = 5 cm.
(iii) Draw the angle bisector of ∠B.
(iv) With centre A and radius 5 cm. draw an arc
which intersects the angle bisector of ∠B at D
(v) Join AD and DC.
ABCD in the required quadrilateral.
On measuring CD, it is 5.3 cm (approx).
Question 20.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB (2001)
Solution:
Steps of Construction :
(i) Draw a line AB = 6 cm
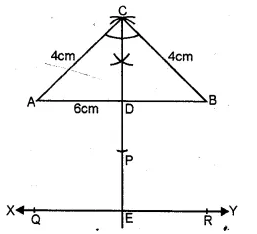
(ii) With centre A and B and radius 4 cm,
draw two arcs intersecting each other at C.
(iii) Join CA and CB
(iv) Draw the bisector of ∠C and cut off CP = 5 cm
(v) Draw a line XY parallel to AB at a distance of 5 cm.
(vi) From P, draw arcs of radius 5 cm each intersecting
the line XY at Q and R. Hence Q and R are the required points.
Question 21.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC, (1995)
Solution:
Steps of Construction :
(i) With centre 0 and radius 4 cm draw a circle.
(ii) Take point A on this circle.
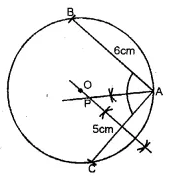
(iii) With centre A and radius 6 cm draw an arc cutting the circle at B.
(iv) Again with radius 5 cm, draw another arc cutting the circle at C.
(v) Join AB and AC.
(vi) Draw the perpendicular bisector of AC.
Any point on it, will be equidistant from A and C.
(vii) Draw the angle bisector of ∠A intersecting
the perpendicular bisector of AC at P. P is the required locus.
Question 22.
Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
(i) Construct a triangle ABC, in which BC = 6 cm, AB = 9 cm. and ∠ABC = 60°.
(ii) Construct the locus of all points, inside ∆ABC, which are equidistant from B and C.
(iii) Construct the locus of the vertices of the triangles with BC as base, which are equal in area to ∆ABC.
(iv) Mark the point Q, in your construction, which would make ∆QBC equal in area to ∆ABC, and isosceles.
(v) Measure and record the length of CQ. (1998)
Solution:
Steps of Construction :
(i) Draw AB = 9 cm
(ii) At B draw an angle of 60° and cut off BC = 6 cm.
(iii) Join AC
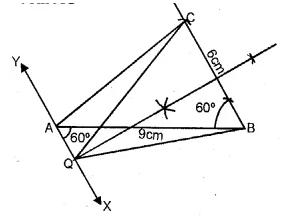
(iv) Draw perpendicular bisector of BC.
All points on it will be equidistant from B and C.
(v) From A, draw a line XY parallel to BC.
(vi) Produce the perpendicular bisector of BC to meet XY in Q.
(vii) Join QC and QB.
∆QBC will be the triangle equal in area to ∆ABC
because these are on the same base BC and between the same parallel lines.
On measuring, the length of CQ is 8.2 cm (approx.).
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Ex 14 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.