ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test
Question 1.
Find the slope of a line whose inclination is
(i) 45°
(ii) 30°
Solution:
(i) tan 45° = 1
(ii) tan 30° = \(\frac { 1 }{ \sqrt { 3 } } \)
Question 2.
Find the inclination of a line whose gradient is
(i) 1
(ii) √3
(iii) \(\frac { 1 }{ \sqrt { 3 } } \)
Solution:
(i) tan θ = 1 ⇒ θ = 45°
(ii) tan θ = √3 ⇒ θ = 60°
(iii) tan θ = \(\frac { 1 }{ \sqrt { 3 } } \) ⇒ θ = 30°
Question 3.
Find the equation of a straight line parallel 1 to x-axis which is at a distance
(i) 2 units above it
(ii) 3 units below it.
Solution:
(i) A line which is parallel to x-axis is y = a
⇒ y = 2
⇒ y – 2 = 0
(ii) A line which is parallel to x-axis is y = a
⇒ y = -3
⇒ y + 3 = 0
Question 4.
Find the equation of a straight line parallel to y-axis which is at a distance of:
(i) 3 units to the right
(ii) 2 units to the left.
Solution:
(i) The equation of line parallel to y-axis is at a distance of 3 units to the right is x = 3 ⇒ x – 3 = 0
(ii) The equation of line parallel to y-axis at a distance of 2 units to the left is x = -2 ⇒ x + 2 = 0
Question 5.
Find the equation of a straight line parallel to y-axis and passing through the point ( – 3, 5).
Solution:
The equation of the line parallel to y-axis passing through ( – 3, 5) to x = -3
⇒ x + 3 = 0
Question 6.
Find the equation of the a line whose
(i) slope = 3, y-intercept = – 5
(ii) slope = \(– \frac { 2 }{ 7 } \), y-intercept = 3
(iii) gradient = √3, y-intercept = \(– \frac { 4 }{ 3 } \)
(iv) inclination = 30°,y-intercept = 2
Solution:
Equation of a line whose slope and y-intercept is given is
y = mx + c
where m is the slope and c is the y-intercept
(i) y = mx + c
⇒ y = 3x + (-5)
⇒ y = 3x – 5
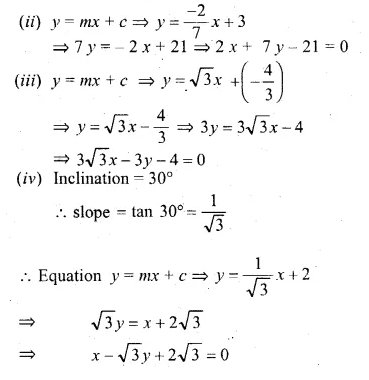
Question 7.
Find the slope and y-intercept of the following lines:
(i) x – 2y – 1 = 0
(ii) 4x – 5y – 9 = – 0
(iii) 3x +5y + 7 = 0
(iv) \(\frac { x }{ 3 } +\frac { y }{ 4 } =1\)
(v) y – 3 = 0
(vi) x – 3 = 0
Solution:
We know that in the equation
y = mx + c, m is the slope and c is the y-intercept.
Now using this, we find,
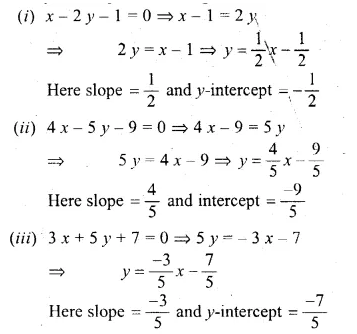

Question 8.
The equation of the line PQ is 3y – 3x + 7 = 0
(i) Write down the slope of the line PQ.
(ii) Calculate the angle that the line PQ makes with the positive direction of x-axis.
Solution:
Equation of line PQ is 3y – 3x + 7 = 0
Writing in form of y = mx + c
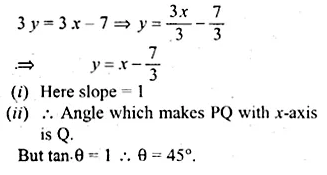
Question 9.
The given figure represents the line y = x + 1 and y = √3x – 1. Write down the angles which the lines make with the positive direction of the x-axis. Hence determine θ.
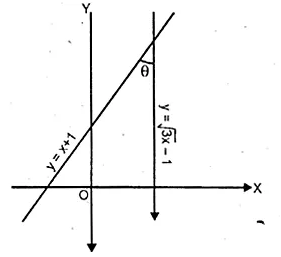
Solution:
Slope of the line y = x + 1 after comparing
it with y = mx + c, m = 1
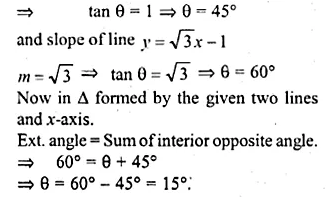
Question 10.
Find the value of p, given that the line \(\frac { y }{ 2 } =x-p\) passes through the point ( – 4, 4) (1992).
Solution:
Equation of line is \(\frac { y }{ 2 } =x-p\)
It passes through the points (-4, 4)
It will satisfy the equation
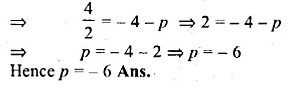
Question 11.
Given that (a, 2a) lies on the line \(\frac { y }{ 2 } =3x-6\) find the value of a.
Solution:
∵ Point (a, 2a) lies on the line
\(\frac { y }{ 2 } =3x-6\)
∴this point will satisfy the equation
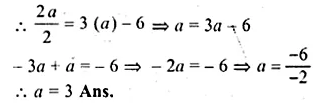
Question 12.
The graph of the equation y = mx + c passes through the points (1, 4) and ( – 2, – 5). Determine the values of m and c.
Solution:
Equation of the line is y = mx + c
∴ it passes through the points (1, 4)
∴ 4 = m x 1 + c
⇒ 4 = m + c
⇒ m + c = 4 … (i)
Again it passes through the point (-2, -5)
∴ 5 = m (-2) + c
⇒ 5 = -2 m + c
⇒ 2m – c = 5 …(ii)
Adding (i) and (ii)
3m = 9
⇒ m = 3
Substituting the value of m in (i)
3 + c = 4
⇒ c = 4 – 3 = 1
Hence m = 3, c = 1
Question 13.
Find the equation of the line passing through the point (2, – 5) and making an intercept of – 3 on the y-axis.
Solution:
∴ The line intersects y-axis making an intercept of -3
∴ the co-ordinates of point of intersection will be (0, -3)
Now the slope of line (m) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
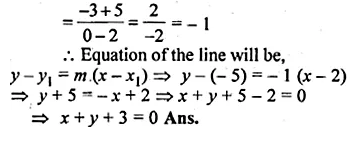
Question 14.
Find the equation of a straight line passing through ( – 1, 2) and whose slope is \(\\ \frac { 2 }{ 5 } \).
Solution:
Equation of the line will be
\(y-{ y }_{ 1 }=m(x-{ x }_{ 1 }) \)
\(y-2=\frac { 2 }{ 5 } (x+1)\)
⇒ 5y – 10 = 2x + 2
⇒ 2x – 5y + 2 + 10 = 0
⇒ 2x – 5y + 12 = 0
Question 15.
Find the equation of a straight line whose inclination is 60° and which passes through the point (0, – 3).
Solution:
The equation of line whose slope is wand passes through a given point is
\(y-{ y }_{ 1 }=m(x-{ x }_{ 1 }) \)
Here m = tan 60° = √3 and point is (0, -3)
∴ y + 3 = √3 (x – 0)
⇒ y + 3 = √3x
⇒ √3x – y – 3 = 0
Question 16.
Find the gradient of a line passing through the following pairs of points.
(i) (0, – 2), (3, 4)
(ii) (3, – 7), ( – 1, 8)
Solution:
m = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
Given
(i) (0, -2), (3, 4)
(ii) (3, -7), (-1, 8)
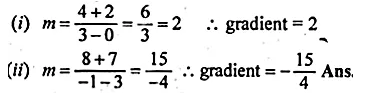
Question 17.
The coordinates of two points E and F are (0, 4) and (3, 7) respectively. Find :
(i) The gradient of EF
(ii) The equation of EF
(iii) The coordinates of the point where the line EF intersects the x-axis.
Solution:
Co-ordinates of points E (0, 4) and F (3, 7) are given, then
(i) The gradient of EF

Question 18.
Find the intercepts made by the line 2x – 3y + 12 = 0 on the co-ordinate axis.
Solution:
Putting y = 0, we will get the intercept made on x-axis,
2x – 3y + 12 = 0
⇒ 2x – 3 × 0 + 12 = 0
⇒ 2x – 0 + 2 = 0
⇒ 2x = -12
⇒ x = -6
and putting x = 0, we get the intercepts made on y-axis,
2x – 3y + 12 = 0
⇒ 2 × 0 – 3y + 12 = 0
⇒ -3y = -12
⇒ \(y= \frac { -12 }{ -3 } \) = 4
Question 19.
Find the equation of the line passing through the points P (5, 1) and Q (1, – 1). Hence, show that the points P, Q and R (11, 4) are collinear.
Solution:
The two given points are P (5, 1), Q(1, -1).
∴ Slope of the line (m)
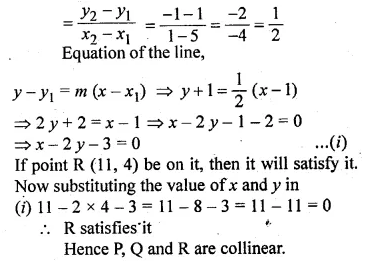
Question 20.
Find the value of ‘a’ for which the following points A (a, 3), B (2,1) and C (5, a) are collinear. Hence find the equation of the line.
Solution:
Given That
A(a, 3), B (2, 1) and C (5, a) are collinear.
Slope of AB = Slope of BC
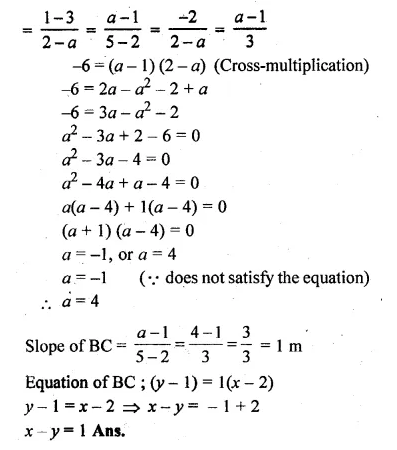
Question 21.
Use a graph paper for this question. The graph of a linear equation in x and y, passes through A ( – 1, – 1) and B (2, 5). From your graph, find the values of h and k, if the line passes through (h, 4) and (½, k). (2005)
Solution:
Points (h, 4) and (½, k) lie on the line passing
through A(-1, -1) and B(2, 5)
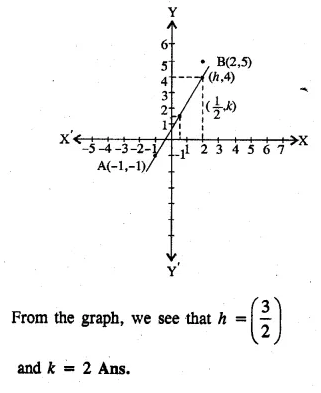
Question 22.
ABCD is a parallelogram where A (x, y), B (5, 8), C (4, 7) and D (2, – 4). Find
(i) the coordinates of A
(ii) the equation of the diagonal BD.
Solution:
Given that
ABCD is a parallelogram where A (x, y), B (5, 8), C (4, 7) and D (2, -4)
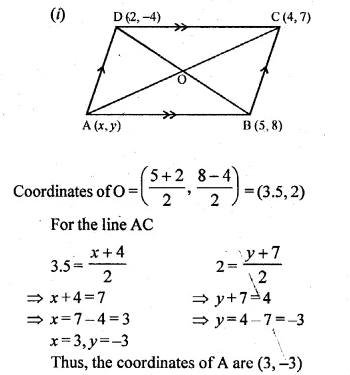
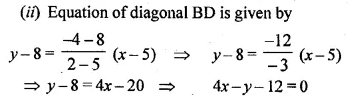
Question 23.
In ∆ABC, A (3, 5), B (7, 8) and C (1, – 10). Find the equation of the median through A.
Solution:
AD is median
⇒ D is mid point of BC
∴ D is \(\left( \frac { 7+1 }{ 2 } ,\frac { 8-10 }{ 2 } \right) \)
i.e (4, -1)
slope of AD
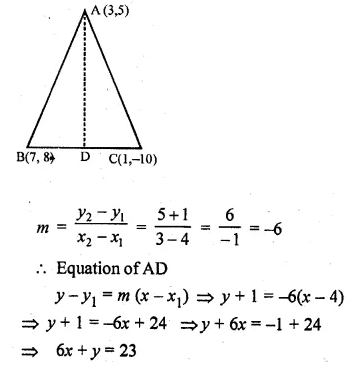
Question 24.
Find the equation of a line passing through the point ( – 2, 3) and having x-intercept 4 units. (2002)
Solution:
x-intercept = 4
∴ Co-ordinates of the point will be (4, 0)
Now slope of the line passing through the points (-2, 3) and (4, 0)
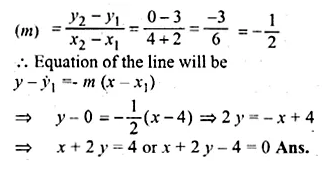
Question 25.
Find the equation of the line whose x-intercept is 6 and y-intercept is – 4.
Solution:
x-intercept = 6
∴ The line will pass through the point (6, 0)
y -intercept = -4 ⇒ c = -4
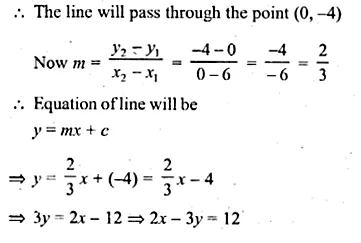
Question 26.
Write down the equation of the line whose gradient is \(\\ \frac { 1 }{ 2 } \) and which passes through P where P divides the line segment joining A ( – 2, 6) and B (3, – 4) in the ratio 2 : 3. (2001)
Solution:
P divides the line segment joining the points
A (-2, 6) and (3, -4) in the ratio 2 : 3
∴ Co-ordinates of P will be
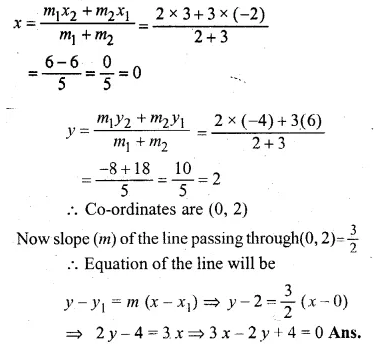
Question 27.
Find the equation of the line passing through the point (1, 4) and intersecting the line x – 2y – 11 = 0 on the y-axis.
Solution:
line x – 2y – 11 = 0 passes through y-axis
x = 0,
Now substituting the value of x in the equation x – 2y – 11 = 0
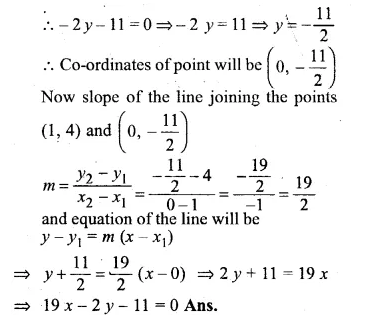
Question 28.
Find the equation of the straight line containing the point (3, 2) and making positive equal intercepts on axes.
Solution:
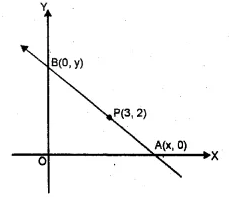
Let the line containing the point P (3, 2)
passes through x-axis at A (x, 0) and y-axis at B (0, y)
OA = OB given
∴ x = y
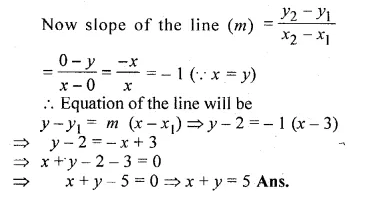
Question 29.
Three vertices of a parallelogram ABCD taken in order are A (3, 6), B (5, 10) and C (3, 2) find:
(i) the coordinates of the fourth vertex D.
(ii) length of diagonal BD.
(iii) equation of side AB of the parallelogram ABCD. (2015)
Solution:
Three vertices of a parallelogram ABCD taken in order are
A (3, 6), B (5, 10) and C (3, 2)
(i) We need to find the co-ordinates of D
We know that the diagonals of a parallelogram bisect each other
Let (x, y) be the co-ordinates of D
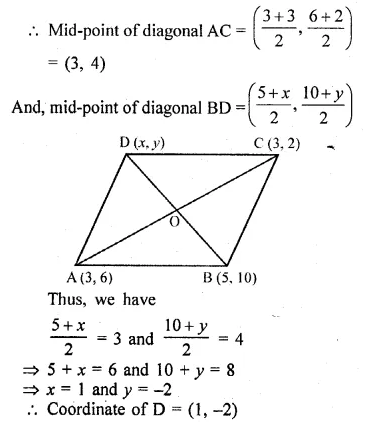

Question 30.
A and B arc two points on the x-axis and y-axis respectively. P (2, – 3) is the mid point of AB. Find the
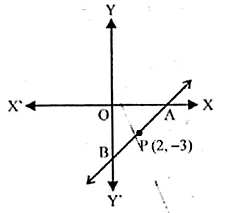
(i) the co-ordinates of A and B.
(ii) the slope of the line AB.
(iii) the equation of the line AB. (2010)
Solution:
Points A and B are on x-axis and y-axis respectively
Let co-ordinates of A be (X, O) and of B be (O, Y)
P (2, -3) is the midpoint of AB
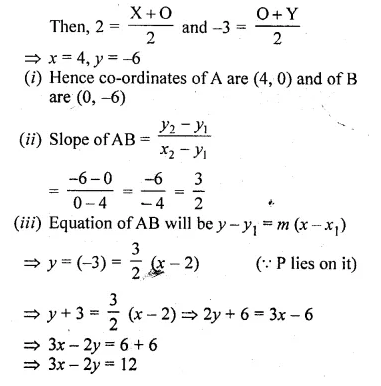
Question 31.
Find the equations of the diagonals of a rectangle whose sides are x = – 1, x = 2 , y = – 2 and y = 6.
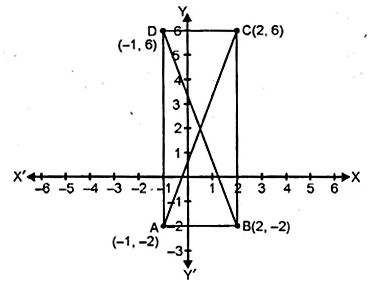
Solution:
The equations of sides of a rectangle whose equations are
x1 = -1, x2 = 2, y1 = -2, y2 = 6.
These lines form a rectangle when they intersect at A, B, C, D respectively
Co-ordinates of A, B, C and D will be
(-1, -2), (2, -2), (2, 6) and (-1, 6) respectively.
AC and BD are its diagonals
(i) Slope of the diagonal AC
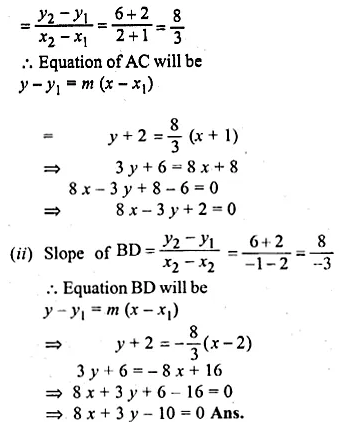
Question 32.
Find the equation of a straight line passing through the origin and through the point of intersection of the lines 5x + 1y – 3 and 2x – 3y = 7
Solution:
5x + 7y = 3 …(i)
2x – 3 y = 7 …(ii)
Multiply (i) by 3 and (ii) by 7,
15x + 21y = 9
14x – 21y = 49
Adding we get,
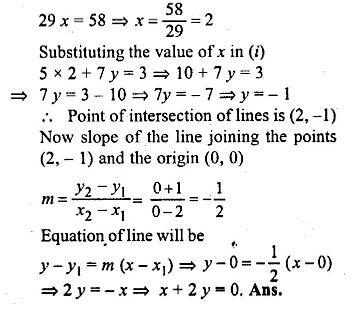
Question 33.
Point A (3, – 2) on reflection in the x-axis is mapped as A’ and point B on reflection in the y-axis is mapped onto B’ ( – 4, 3).
(i) Write down the co-ordinates of A’ and B.
(ii) Find the slope of the line A’B, hence find its inclination.
Solution:
A’ is the image of A (3, -2) on reflection in the x-axis.
∴ Co-ordinates of A’ will be (3, 2)
Again B’ (- 4, 3) in the image of A’, when reflected in the y-axis
∴ Co-ordinates of B will be (4, 3)
(ii) Slope of the line joining, the points A’ (3, 2) and B (4, 3)
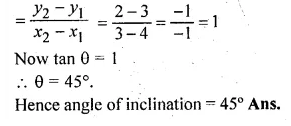
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.